Оптимальное управление линейной непрерывной системой при наличии аддитивных возмущений

Изложенный выше метод синтеза оптимального управ­ления с использованием понятия достаточных координат может быть обобщен и на случай управления непрерывными системами. В качестве примера рассмотрим задачу синтеза оптимального управления линейной системой

Однако в отличие от случая управления при полной информации теперь полагаем, что вектор х непосредственно измерен быть не может. Измерению доступен некоторый вектор у, связанный с век­тором х линейным соотношением 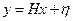, где —вектор ошибок измерения.

В качестве критерия оптимальности примем математическое ожидание взвешенной суммы энергетических затрат и конечной точности

Считаем, что , белые гауссовские шумы с характеристиками

Возможны два подхода к решению задачи. Первый заключает­ся в дискретизации исходной задачи и применении полученного выше решения. В этом случае дискретными аналогами являются следующие соотношения:

где

причем

Применительно к данным соотношениям дискретный фильтр Калмана будет иметь вид (3.53), (3.54). Устремляя At к нулю, по­лучаем дифференциальные уравнения для апостериорных математи­ческих ожиданий и корреляционной матрицы вектора

представляющие собой уравнения непрерывного фильтра Кал­мана.

Как и в дискретном случае, апостериорная корреляционная матрица Р* может быть определена заранее, так как она не зави­сит от конкретных значений управлений и измерений. Поэтому вектор апостериорного математического ожидания х* может рас­сматриваться в качестве вектора достаточных координат.

Аналогичным способом получим и алгоритм оптимального уп­равления. Согласно результатам предыдущего раздела для дискретизированной задачи (6.15) можно записать следующее выражение для функции будущих потерь

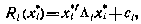
где

Здесь

Алгоритм оптимального управления при этом имеет вид

Устремляя , получаем непрерывные аналоги:

— для функции будущих потерь

причем матрица и параметр с удовлетворяют следующей систе­ме дифференциальных уравнений:

— для алгоритма оптимального управления

Алгоритм оптимального управления является линейным и по структуре совпадает с соответствующим алгоритмом оптимального детерминированного управления. Иными словами, теорема разде­ления для линейных систем с аддитивными возмущениями и квад­ратичным критерием справедлива как в дискретном, так и в непре­рывном случае.

Синтезированная оптимальная система управления включает в себя последовательное соединение непрерывного фильтра Кал-мана, определяемого уравнениями (6.16), и управляющего устрой­ства, реализующего алгоритм (6.17).

Второй подход к решению рассматриваемой задачи заключает­ся в непосредственном применении стохастического уравнения Беллмана (5.76). С этой целью исходную задачу переформулируем в терминах достаточных координат. Другими словами, рассмотрим систему, описываемую уравнением

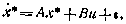
где

Критерий оптимальности преобразуем к виду

Уравнение Беллмана, соответствующее данной задаче, прини­мает вид

с граничным условием

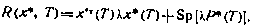
В соответствии с определениями (5.77) устанавливаем, что в данном случае вектор коэффициентов сноса и матрица коэффициентов диффузии равны

Уравнение (6.18) с точностью до обозначений совпадает с соответ­ствующим уравнением Беллмана для случая управления при пол­ной информации. Поэтому и его решение будет иметь аналогичный вид:

причем

Алгоритм оптимального управления при этом принимает вид

что полностью совпадает с алгоритмом (6.17).