Статистическая зависимость. Корреляция и регрессия. Элементы дисперсионного анализа

Как известно, случайные величины X и Y могут быть либо зависимыми, либо независимыми. Существуют следующие формы зависимости – функциональная и статистическая. В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y=f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Однако, если X и Y случайные величины, то между ними может существовать зависимость иного рода, называемая статистической. Дело в том, что на формирование значений случайных величин X и Y оказывают влияние различные факторы. Под воздействием этих факторов и формируются конкретные значения X и Y. Допустим, что на Х и У влияют одни те же факторы, например Z1, Z2, Z3, тогда X и Y находятся в полном соответствии друг с другом и связаны функционально. Предположим теперь, что на X воздействуют факторы Z1, Z2, Z3, а на только Y и Z1, Z2. Обе величины и X и Y являются случайными, но так как имеются общие факторы Z1 и Z2, оказывающие влияние и на X и на Y, то значения X и Y обязательно будут взаимосвязаны. И связь это уже не будет функциональной: фактор Z3, влияющий лишь на одну из случайных величин, разрушает прямую (функциональную) зависимость между значениями X и Y, принимаемыми в одном и том же испытании. Связь носит вероятностный случайный характер, в численном выражении меняясь, от испытания к испытанию, но эта связь определенно присутствует и называется статистической. При этом каждому значению X может соответствовать не одно значение Y, как при функциональной зависимости, а целое множество значений.

ОПРЕДЕЛЕНИЕ. Зависимость случайных величин называют статистической, если изменения одной из них приводит к изменению закона распределения другой.

ОПРЕДЕЛЕНИЕ. Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные коррреляционной зависимостью, оказываются коррелированными.

Именно корреляционные зависимости наиболее часто встречаются в природе в силу взаимовлияния и тесного переплетения огромного множества самых различных факторов, определяющих значения изучаемых показателей.

Корреляционную зависимость Y от X можно описать с помощью уравнения вида:

yx=f(x) (1)

где yx - условное среднее величины Y, соответствующее значению x величины X, а f(x) некоторая функция. Уравнение (1) называется выборочным уравнением регрессии Y на X. Функцию f(x) называют выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X.

Совершенно аналогично выборочным уравнением регрессии X на Y является уравнение: xy=φ(y)

В зависимости от вида уравнения регрессии и формы соответствующей линии регрессии определяют форму корреляционнной зависимости между рассматриваемыми величинами – линейной, квадратической, показательной, экспоненциальной.

Важнейшим является вопрос выбора вида функции регрессии f(x) [или φ(y)], например линейная или нелинейная (показательная, логарифимическая и т.д.)

На практике вид функции регрессии можно определить, построив на координатной плоскости множество точек, соответствующих всем имеющимся парам наблюдений (x;y).

Рис. 1. Линейная регрессия значима. Модель Y=a+bX.

Рис. 2. Линейная регрессия незначима. Модель Y=

Рис. 3. Линейная регрессия значима. Нелинейная модель (y=ax2+bx+c)

Например, на рис.1. видна тенденция роста значений Y с ростом X, при этом средние значения Y располагается визуально на прямой. Имеет смысл использовать линейную модель (вид зависимости Y от X принято называть моделью) зависимости Y от X. На рис.2. средние значения Y не зависят от x, следовательно линейная регрессия незначима (функция регрессии постоянна и равна). На рис. 3. прослеживается тенденция нелинейности модели.В частности, если изменение одной из величин изменяет среднее значение другой, то такая статистическая зависимость называется корреляционной.

Сущность дисперсионного анализа состоит в проверке гипотезы о тождественности выборочных дисперсий одной и той же генеральной дисперсии.

Дисперсия характеризует важные конструкторские и технологические показатели как:

точность приборов;

рассеивание точек попадания при стрельбе и др.

И еще дисперсионный анализ одновременно решает проблему проверки гипотезы о равенстве средних значений выборок.

Задача сравнения дисперсий сводится к проверке исходной гипотезы (нулевой гипотезы) о принадлежности двух выборок одной и той же генеральной совокупности.

Для проверки гипотезы о равенстве дисперсий нужно иметь независимую функцию, вычислимую по данным эксперимента.

Такой функцией является функция Фишера (распределение Фишера, F -распределение), определяемая так:

Где U и V случайные величины, имеющие распределение ;

k₁ и k₂ соответствующие степени свободы случайных величин U и V соответственно, , ;

N₁ и N₂ - количество испытаний (объемы выборок).

является мерой сравнения дисперсий потому, что дисперсии, являясь суммой квадратов ошибок, имеют распределение.

Распределение хи-квадрат определяется следующим образом:

Где v - число степеней свободы, e- число Эйлера (2,71…), Г - гамма-функция.

График плотности F -распределения показан на рис. 5.2.

Итак, случайная величина

где и - несмещенные оценки дисперсий, полученных из независимых выборок, взятых из нормальных совокупностей, имеет распределение Фишера (F -распределение).

Рис. 5.2. График плотности F -распределения

Величина F - случайна, поэтому судить однозначно по ее величине о подтверждении или опровержении гипотезы об однородности исследуемых выборок нельзя.

Поэтому вводится q уровень значимости, численно равный вероятности неприемлемых отклонений от принятой гипотезы. Области неприемлемых значений F показаны на рис. 5.2 штриховкой. Граничные точки допустимых значений F определяются точками F₁ и F₂, соответствующих вероятностям q/2.

Если вычисленное по данным эксперимента значение F попадает в область между точками F₁ и F₂:

то принятая гипотеза не опровергается.

Заметим, что случайная величина

также имеет F -распределение со степенями свободы и соответственно. Следовательно, вероятность попадания числа F в левую критическую область равна:

Отсюда следует, что левая критическая точка F -распределения соответствует правой критической точке F* -распределения. Т. е. правые точки распределений F и F* определяют левую и правую точки F₁ и F₂. Поэтому в таблицах представлены только правые F₂ критические точки F -распределения.

В таблицах значения F₂ приведены в зависимости от q/2, числа степеней свободы и .

Обычно при вычислении F в числитель отношения 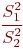ставят значение большей дисперсии.

Итак, при принятая гипотеза не опровергается, при - не подтверждается.

Чем меньше уровень значимости q, тем меньше вероятность забраковать проверяемую гипотезу, когда она верна, т. е. совершить ошибку первого рода.

Но с уменьшением уровня значимости (увеличения F₂) расширяется область допустимых ошибок, что приводит к увеличению вероятности принятия неверного решения, т. е. совершения ошибки второго рода.

В заключение изложенного отметим, что как бы ни был велик объем статистического материала и критерий Фишера (впрочем, как и любой другой) не может дать абсолютно достоверный ответ о справедливости или несправедливости проверяемой гипотезы, так как мы оперируем случайными числами.

То есть, опровержение гипотезы ни в коем случае не означает категорического, логического опровержения гипотезы при F>F₂, равно как и подтверждение гипотезы при не означает категорического доказательства ее справедливости. Не исключено, что в том и в другом случае решение может оказаться ошибочным.

Суждение о подтверждении или отклонении выдвинутой гипотезы высказывается с определенной степенью достоверности.