Лабораторная работа 1
ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПИ, СОДЕРЖАЩЕЙ ОДИН РЕАКТИВНЫЙ ЭЛЕМЕНТ И РЕЗИСТОР
Цель работы
Экспериментальное исследование переходных процессов в RC -цепи при воздействии прямоугольного импульса напряжения.
Задание на самостоятельную подготовку к работе
2.1. Изучите методы и результаты анализа переходных процессов в цепи, содержащей резистор и конденсатор.
2.2. Рассчитайте и постройте кривые изменения напряжений 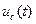 и
и 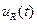 для значений R 1, C 1, соответствующие вашему номеру варианта (табл.1.1). Данные расчета занесите в табл.1.3. Для анализа переходного процесса при воздействии одиночного прямоугольного импульса удобно воспользоваться методом наложения, представив импульс суммой двух смещенных во времени скачков напряжения (рис.1.1), и записать искомую реакцию в следующем виде:
для значений R 1, C 1, соответствующие вашему номеру варианта (табл.1.1). Данные расчета занесите в табл.1.3. Для анализа переходного процесса при воздействии одиночного прямоугольного импульса удобно воспользоваться методом наложения, представив импульс суммой двух смещенных во времени скачков напряжения (рис.1.1), и записать искомую реакцию в следующем виде:
0≤ t ≤ t и y 1(t) = y (t)
t ≥ t и y 2(t) = y (t) - y (t - t и)


Рис. 1.1
где y (t) - реакция исследуемой цепи при воздействии постоянного напряжения 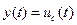 или
или  . Например, напряжение на емкости при включении цепи RC на постоянное напряжение U 1
. Например, напряжение на емкости при включении цепи RC на постоянное напряжение U 1
 = U 1 (1 - e- t /τ), где τ = RC - постоянная времени цепи.
= U 1 (1 - e- t /τ), где τ = RC - постоянная времени цепи.
Следовательно, при воздействии прямоугольного импульса
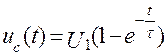 при 0≤ t ≤ t и
при 0≤ t ≤ t и
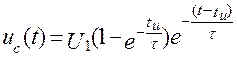 при t ≥ t и (1.1)
при t ≥ t и (1.1)
Выражение для тока i(t) и напряжения на резисторе 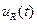 легко получить из (1.1) простым дифференцированием:
легко получить из (1.1) простым дифференцированием:
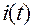 = C
= C 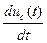 ,
,  . (1.2)
. (1.2)
Кривые 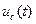 и
и 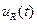 при воздействии прямоугольного импульса напряжения на цепь приведены на рис. 1.2.
при воздействии прямоугольного импульса напряжения на цепь приведены на рис. 1.2.

Риc.1.2
В интервале времени 0≤ t ≤ t и конденсатор заряжается и напряжение 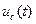 растет. В свободном режиме t > t и происходит разряд конденсатора, и напряжение
растет. В свободном режиме t > t и происходит разряд конденсатора, и напряжение 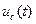 убывает. Направление тока при этом противоположно направлению тока при заряде, что обуславливает скачок на кривой
убывает. Направление тока при этом противоположно направлению тока при заряде, что обуславливает скачок на кривой 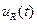 при t= t и (рис.1.2).
при t= t и (рис.1.2).
Длительность разряда конденсатора (переходного процесса) практически определяется интервалом времени (3-5) τ.
Постоянная времени легко определяется графически по любой реакции, характеризующей переходный процесс. Численно она равна длине подкасательной или определяется на уровне 0,63 U 1 по кривой 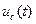 на уровне 0,37 U 1 по кривой
на уровне 0,37 U 1 по кривой 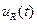 (рис. 1.2).
(рис. 1.2).
2.3. Используя приведенные соотношения и данные табл. 1.1 для свого номера варианта, рассчитайте постоянную времени цепи для шести комбинаций R и С и заполните табл. 1.2. Сопротивление R 3 (рис. 1.3) в расчетах не учитывать, так как R 3 много меньше R.
Таблица 1.1
Значения параметров RC цепи
| Номер варианта | Т сл, мкс | t и, мкс | R 1, Ом | R 2, Ом | C 1, мкФ | C 2, мкФ | C 3, мкФ |
| 0,10 | 0.036 | 0,28 | |||||
| 0,08 | 0,028 | 0,22 | |||||
| 0,12 | 0,04 | 0,36 | |||||
| 0,057 | 0,019 | 0,17 | |||||
| 0,072 | 0,024 | 0,21 | |||||
| 0,048 | 0.016 | 0,14 | |||||
| 0,075 | 0,027 | 0,21 | |||||
| 0,069 | 0,023 | 0,20 | |||||
| 0,058 | 0,02 | 0,16 | |||||
| 0,03 | 0,01 | 0,09 | |||||
| 0,056 | 0,019 | 0,16 | |||||
| 0,036 | 0.012 | 0,11 | |||||
| 0,034 | 0.013 | 0.18 |
Таблица 1.2
Таблица расчетных и экспериментальных данных
| Задано | R 1= Ом | R 2= Ом | |||||
| С 1= | С 2= | С 3= | С 1= | С 2= | С 3= | ||
| мкФ | мкФ | мкФ | мкФ | мкФ | мкФ | ||
| Теоретически | τ, мкс | ||||||
| Эксперимен- тально | τ, мкс |
Таблица 1.3
Данные предварительного расчета
| 0 ≤ t ≤ t и | t ≥ t и | ||||||||
| t /τ | t, мкс | 
|  , В , В
| 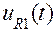 , В , В
| 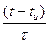
| t, мкс | 
|  , В , В
| 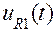 , В , В
|
| 0,67 | 0,67 | ||||||||
| 1,00 | 1,00 | ||||||||
| 1,33 | 1,33 | ||||||||
| 2,00 | 2,40 | ||||||||
| 2,40 | 3,00 | ||||||||
| 3,00 | 5,00 |
 2017-11-01
2017-11-01 183
183







