Лекция 16
Энергия электрического поля
Энергия системы зарядов
Найдем сначала выражение для потенциальной энергии системы двух точечных зарядов 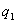 и
и 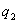 , находящихся на расстоянии
, находящихся на расстоянии 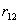 . Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние
. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние 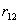 . При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая
. При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая 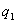 к
к 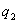 либо
либо 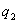 к
к 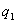 .Работа переноса заряда
.Работа переноса заряда 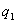 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 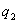 на
на 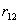

где 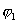 - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 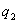 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 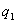 . Аналогично работа переноса заряда
. Аналогично работа переноса заряда 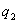 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 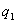 на
на 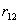 , равна
, равна

где 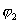 - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 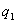 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 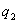 . Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы
. Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы
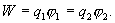
Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:

Эта формула дает энергию системы двух зарядов. Перенесем из бесконечности еще один заряд  и поместим его в точку, находящуюся на расстоянии
и поместим его в точку, находящуюся на расстоянии  от
от 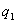 и
и 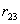 от
от 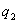 . При этом совершим работу
. При этом совершим работу
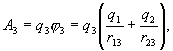
где 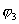 - потенциал, создаваемый зарядами
- потенциал, создаваемый зарядами 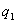 и
и 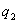 в той точке, в которую мы поместили заряд
в той точке, в которую мы поместили заряд  . В сумме с
. В сумме с  или
или  работа
работа  будет равна энергии трех зарядов:
будет равна энергии трех зарядов:

Последнее выражение можно привести к виду
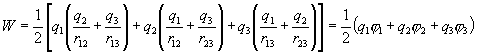
Добавляя к системе Зарядов последовательно 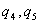 и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
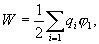 | (16.1) |
где 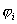 - потенциал, создаваемый в той точке, где находится
- потенциал, создаваемый в той точке, где находится 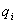 , всеми зарядами, кроме i-го.
, всеми зарядами, кроме i-го.
 2017-10-25
2017-10-25 2918
2918