Спектры периодических сигналов

Балтийский федеральный университет имени И. Канта

Физико-технический факультет

 

Утверждаю

Заведующий кафедры

к.т.н., доцент

А. Шпилевой

«___»_________ 200__ г.

 

 

Л Е К Ц И Я № 7

Тема: «Спектральное представление сигналов»

Текст лекции по дисциплине: «Теория электрической связи»

 

Обсуждена и одобрена на заседании кафедры

протокол №___ от «___»___________200__г.

 

 

Г. Калининград 2012 г.

Текст лекции № 6

по дисциплине: «Теория электрической связи»

 

Введение

Электрические сигналы связи – меняющиеся со временем сигналы напряжения или тока, обычно описываемые во временной области. С другой стороны, подобные сигналы также удобно описывать в частотной области, где описание сигнала называется его спектром. Спектральные понятия достаточно важны при анализе и проектировании систем связи, они могут описывать сигнал через его среднюю мощность или энергетическое содержание на различных частотах и показывают, какую часть электромагнитного спектра занимает сигнал. Частотные спектральные характеристики можно приписать, как и собственно сигналам, так и электрическим схемам. Если говорится, что конкретный спектр описывает конкретный сигнал, подразумевается, что один из способов описания сигнала – это задать его амплитуду и фазу как функцию частоты. В то же время. Когда мы говорим о спектральных параметрах схемы, имеем в виду передаточную функцию, связывающую выход схемы с её входом, т. е. схема характеризуется тем, какая часть спектра входного сигнала пройдёт на выход.

 

Спектры периодических сигналов.

Периодическими называют сигналы, обладающие следующим свойством:

 

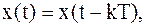	(1)
где	T	–	период;
	k = 0, 1, 2, 3 …

 

Как известно из курса высшей математики, такие функции, удовлетворяющие условиям Дирихле, можно описать суммой тригонометрического ряда (ряда Фурье):

 

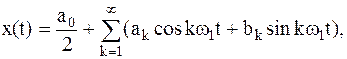	(2)
где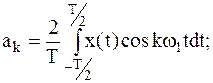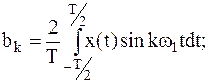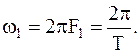

 

Формула (2) ряда Фурье удобна с точки зрения простоты вычисления коэффициентов разложения 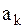и 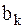. Ряд Фурье можно записать иначе:

 

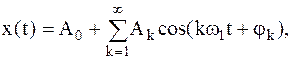	(3)
где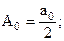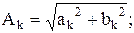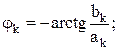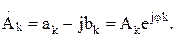

 

Совокупность амплитуд 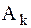называют амплитудным, а совокупность фаз 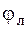– фазовым спектрами. Их можно изображать графически (рис. 1).

 

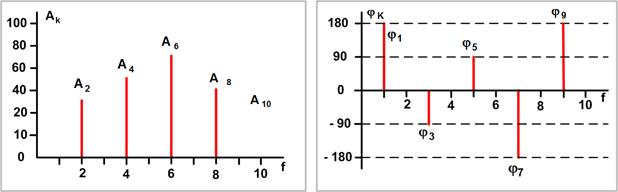Рисунок 1 – Амплитудный и фазовый спектры

 

Амплитудный и фазовый спектры сигнала в совокупности определяют его форму (временную зависимость).

Наиболее компактной является запись ряда Фурье в комплексной форме:

 

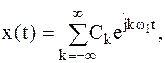	(4)
где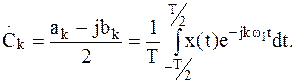

 

Комплексный спектр (4) можно интерпретировать как представление 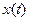в виде сумм спектральных составляющих 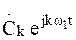, каждая из которых представляет пару гармонических колебаний с половинной амплитудой 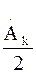на положительной 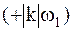и отрицательной 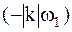частотах. Для вещественных функций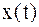 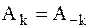– амплитудный спектр – чётная функция частоты, 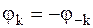– фазовый спектр – нечётная функция частоты.

Ряд Фурье является частным случаем обобщённого ряда Фурье при выборе в качестве базиса совокупности тригонометрических 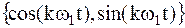или экспоненциальных 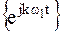функций.

 

Выводы

1. Математическим аппаратом спектрального анализа периодических сигналов является ряд Фурье.

2. Спектры периодических сигналов дискретные (линейчатые), представляют совокупность амплитуд и фаз гармонических колебаний.