Основные понятия и определения. При решении задачи минимизации существенную роль играют понятия импликанты, имплиценты и простой имплиценты

При решении задачи минимизации существенную роль играют понятия импликанты, имплиценты и простой имплиценты.

Рассмотрим три полностью определенные функции f(x), g(x) и d(x). Функция f(x) определена на множестве единичных наборов M ₁[ f (x)] и множестве нулевых наборов M ₀[ f (x)].

Функция g(x) определена на множестве единичных наборов M ₁[g(x)], а функция d(x) - на множестве нулевых наборов M ₀[d(x)].

Логическая функция g(x) называется импликантой логической функции f(x), если множество единичных наборов функции g(x) совпадает или является подмножеством множества единичных наборов функции f(x), т.е.

 

M ₁[g(x)]Í M ₁[ f (x)].

 

Логическая функция d(x) называется имплицентой логической функции f(x), если множество нулевых наборов функции d(x) совпадает или является подмножеством множества нулевых наборов функции f(x) т.е.

 

M ₀[d(x)]Í M ₀[ f (x)].

 

Например, логическая функция g(x) = 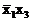является импликантой логической функции

,

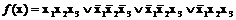так как множество M ₁[g(x)] составляют наборы 100 110, которые входят в множество M ₁[ f (x)]. Аналогично логическая функция 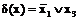является имплицентой этой же логической функции f(x), так как множество M ₀[d(x)]составляют наборы 001 и 011, которые входят во множество M ₀[ f (x)].

Простой импликантой функции f(x) называется любая элементарная функция g(x), являющаяся импликантой этой функции и обладающая тем свойством, что никакая ее собственная часть (т.е. конъюнкция, получаемая из элементарной путем исключения одной или нескольких переменных или их отрицаний) уже не является импликантой данной функции.

Следует обратить внимание, что простой импликантой может быть только элементарная конъюнкция. Докажем это утверждение.

Пусть 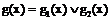есть импликанта функции f(x), т.е.

 

M ₁[g(x)]Í M ₁[ f (x)],

где

M ₁[g(x)]= M ₁[g1(x)] .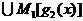

Отсюда следует, что

 

M ₁[g1(x)]Í M ₁[ f (x)];

 

M ₁[g2(x)]Í M ₁[ f (x)].

Следовательно, функци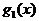и и 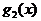также являются импликантами функции f(x), а поэтому функция g(x) не может быть простой импликантой. Например, для логической функции

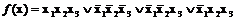
функция 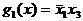является простой импликантой, так как после исключения из 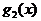переменной 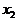получим импликанту .

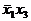Простой имплицентой функции f (x) называется элементарная дизъюнкция d(x), являющаяся имплицентой этой функции и обладающая тем свойством, что никакая ее собственная часть (т.е. дизъюнкция, получаемая из элементарной дизъюнкции путем исключения одной или нескольких переменных или их отрицаний), уже не является имплицентой этой функции. Например, для СКНФ логической функции

,

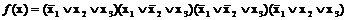функция 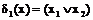является простой имплицентой, а функция 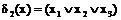не является простой имплицентой, так как после исключения из 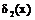переменной 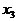получим более короткую имплиценту (.

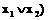Предположим, что на некотором наборе 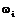значений переменных логическая функция 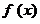принимает значение, равное единице (нулю). Условимся, что эта 1 (0) накрывается импликантой g(x) (имплицентой d(x) функции 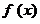, если на наборе 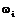импликанта g(x) (имплицента 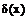) также равна единице (нулю).

Система импликант (имплицент) функции 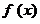называется полной, если все единичные (нулевые) значения функции 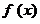накрываются хотя бы одной импликантой(имплицентой) системы.

Пусть система импликант 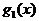, ,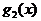..., 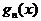является полной системой импликант функции 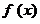. Тогда

 

... = .

 

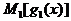
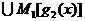
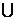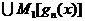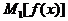Отсюда следует, что дизъюнкция полной системы простых импликант функции 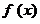образует функцию, эквивалентную 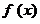. Для полной системы простых имплицент справедливо равенство

... = ,

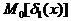
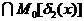
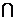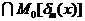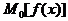т.е. конъюнкция полной системы простых имплицент образует функцию, эквивалентную функции .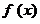

Дизъюнкция (конъюнкция) всех простых импликант (имплицент) логической функции называется сокращенной дизъюнктивной (конъюнктивной) нормальной формой этой функции. Например, для логической функции

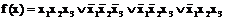
простыми импликантами являются

;

;

,

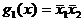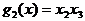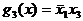а сокращенная ДНФ этой функции имеет вид

= .

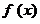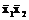
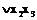
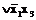Для этой же функции простыми имлицентами являются

;

;

,

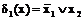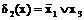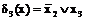а сокращенная КНФ этой функции имеет вид

.

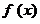
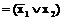
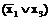
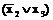Представление любой логической функции в виде сокращенной ДНФ (КНФ) является единственным.

Система простых импликант (имплицент) логической функции называется приведенной, если эта система полная, и любая ее часть не является полной системой импликант (имплицент) этой функции.

Дизъюнкция (конъюнкция) простых импликант (имплицент), составляющих приведенную систему импликант (имплицент) функции, называется ее тупиковой дизъюнктивной (конъюнктивной) нормальной формой - ТДНФ (ТКНФ). Например, для логической функции

=

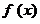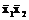
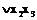
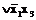
простыми импликантами, составляющими приведенную систему, являются

;

,

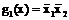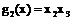а ТДНФ этой функции имеет вид

= .

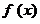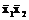
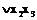Приведенная система имплицент этой функции включает:

;

,

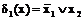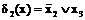а ТКНФ этой функции имеет вид

.

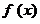
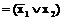
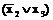Логическая функция может быть представлена одной или несколькими ТДНФ и ТКНФ. ТДНФ (ТКНФ) логической функции, содержащая наименьшее возможное число букв (переменных и их отрицаний), называется минимальной дизъюнктивной (конъюнктивной) нормальной формой - МДНФ (МКНФ).