При решении задач минимизации логических функций, зависящих от небольшого числа переменных, находят широкое применение графические методы. Наиболее применимы эти методы для минимизации логических функций четырех переменных, однако при соответствующих навыках они могут быть использованы для минимизации логических функций, зависящих и от пяти-шести переменных. При большем числе переменных эти методы теряют свое основное свойство - наглядность - и становятся неэффективными.
Карта Карно представляет собой двухвходовую таблицу, соседним строкам и столбцам которой поставлены в соответствие соседние наборы значений переменных логической функции. Кроме того, соседними являются наборы, поставленные в соответствие крайним левому и правому столбцам, а также верхней и нижней строкам.
Например, на рис. 3.1.,а представлена карта Карно для функции четырех переменных, на которой задана логическая функция
 [01, 02, 04, 05, 13, 17 {9, 10, 14}]
[01, 02, 04, 05, 13, 17 {9, 10, 14}]  .
.
Применение карт Карно для представления и минимизации логических функций основано на использовании способностей человека к быстрому построению зрительных образов-контуров. Это позволяет непосредственно по представленной на карте Карно логической функции записать ее сокращенную и тупиковые (как дизъюнктивные, так и конъюнктивные) нормальные формы.
| x5x4 | x3x2x1 | |||||||
| ~ | ~ | ~ | ~ | |||||
| ~ | ~ | |||||||
| ~ | ~ | ~ | ~ | |||||
| ~ | ~ | ~ | ~ | ~ | ~ |
| x4x3 | x2x1 | |||
| ~ | ||||
| ~ | ~ |
Рис. 3.1. Карты Карно для логических функций четырех (а) и пяти (б) переменных
Условимся называть клетки Карно, в которых представлены единичные значения функции, единичными, а клетки, соответствующие нулевым или неопределенным значениям функции, - нулевыми или неопределенными клетками.
При решении задач минимизации логических функций важную роль играют понятия простой импликанты (имплиценты) логической функции. Установим эквивалентные им геометрические образы (контуры) на карте Карно. Обратимся к логической функции 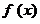 . Конъюнкции
. Конъюнкции  и
и  являются импликантами этой функции. Определим рабочие и условные наборы функции
являются импликантами этой функции. Определим рабочие и условные наборы функции 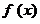 , которые накрываются этими импликантами, и построим на карте Карно (рис. 3.1,а) контуры, которые охватывают клетки, соответствующие этим наборам. Импликанте
, которые накрываются этими импликантами, и построим на карте Карно (рис. 3.1,а) контуры, которые охватывают клетки, соответствующие этим наборам. Импликанте 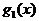 соответствует контур 1, а импликанте
соответствует контур 1, а импликанте 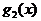 - контур2.
- контур2.
Из рассмотренного примера можно сделать вывод, что любой импликанте логической функции, которая представлена на карте Карно, можно поставить в соответствие контур, охватывающий единичные или единичные и неопределенные клетки.
Если импликантой логической функции является элементарная конъюнкция, то в соответствующий ей контур войдут клетки соседних наборов, допускающих склеивание. Такие контуры мы будем называть правильными контурами карты Карно. Правильные контуры могут включать 1, 2, 4,..., 2  клеток карты Карно, соответствующих единичным или единичным и неопределенным наборам логической функции. Соседним клеткам карты Карно поставлены в соответствие соседние наборы и поэтому на картах Карно легко различаются правильные контуры. На рис. 3.1,б показаны примеры правильных 1, 2, 4 и 8-клеточных правильных контуров для карты Карно, соответствующей логической функции пяти переменных.
клеток карты Карно, соответствующих единичным или единичным и неопределенным наборам логической функции. Соседним клеткам карты Карно поставлены в соответствие соседние наборы и поэтому на картах Карно легко различаются правильные контуры. На рис. 3.1,б показаны примеры правильных 1, 2, 4 и 8-клеточных правильных контуров для карты Карно, соответствующей логической функции пяти переменных.
Чем короче элементарная конъюнкция, являющаяся импликантой логической функции, тем большее количество соседних наборов она покрывает, и, следовательно, тем большее количество соседних клеток должен охватывать соответствующий ей на карте Карно контур. На основании изложенного нетрудно установить признаки контуров карты Карно, соответствующих простой импликанте логической функции.
Простой импликанте логической функции соответствует максимально правильный контур, охватывающий единичные или единичные и неопределенные клетки карты Карно. Отличительным признаком максимально возможного правилного контура является то, что он не может быть составной частью другого правидьного контура. Максимальный правильный контур карты Карно, охватывающий хотя бы одну единичную клетку, соответствует существенной простой импликанте логической функции. Чтобы с помощью карты Карно успешно решать задачи минимизации логических функций, необходимо знать и уметь различать типичные конфигурации правильных максимальных контуров. На рис. 3.2, б показаны типичные конфигурации четырехклеточных максимальных правильных контуров. Особое внимание следует обращать на
| x4x3 | x2x1 | |||
| x3x4 | x2x1 | |||
| x4x3 | x2x1 | |||
| ~ | ||||
а б в
Рис. 3.2 Типичные двухклеточные (а), четырехклеточные (б) и восьмиклеточные (в) контуры на картах Карно четырех переменных
контуры, которые имеют видимый разрыв, так как объединяемые ими соседние клетки находятся в крайних строках или столбцах карты Карно. Типичные восьмиклеточные максимальные правильные контуры показаны на рис. 3.2, в. На картах Карно для функций четырех переменных эти конфигурации распознаются легче всего.
При минимизации с помощью карт Карно логических функций пяти переменных трудности возрастают, так как правильные контуры на этих картах могут терпеть разрывы не только по краям, но и внутри карты Карно, поскольку каждая клетка такой карты имеет одну соседнюю клетку, которая расположена отдельно.
Чтобы по виду максимального правильного контура определить аналитическую форму записи простой импликанты, необходимо определить те переменные логической функции, которые в пределах рассматриваемого максимального контура сохраняют свои значения. Если переменная сохраняет свое значение во всех клетках контура и равна единице, то она входит в выражение простой импликанты. Если переменная сохраняет свое значение во всех клетках контура и равна нулю, то в выражение простой импликанты входит ее инверсия. Переменные, которые в пределах рассматриваемого контура изменяют свое значение, не включаются в выражение простой импликанты, так как они поглощаются при склеивании соседних наборов, объединяемых в контуре.
Пример 3.5. Определим выражение для простой импликанты, соответствующей максимальному правильному контуру 1 (рис. 3.2,б). В пределах рассматриваемого контура сохраняют свои значения переменные  и
и 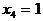 . Следовательно, простая импликанта имеет вид
. Следовательно, простая импликанта имеет вид
 .
.
Проведя аналогичные рассуждения для контуров 2 и 3 (рис. 3.2,б), простые импликанты можно представить в виде
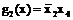 ;
;
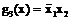 .
.
Пользуясь рассмотренной методикой определения простых импликант, можно с помощью карт Карно определять сокращенные и тупиковые дизъюнктивные нормальные формы логических функций.
Правило получения сокращенной и тупиковой дизъюнктивных нормальных форм состоит в следующем.
Для получения сокращенной ДНФ логической функции по карте Карно необходимо найти все правильные контуры, охватывающие единичные клетки, выписать соответствующие им простые импликанты и объединить их знаком дизъюнкции.
При минимизации неполностью определенных логических функций контуры могут охватывать клетки, соответствующие условным наборам, однако каждый выделенный максимальный контур должен охватывать хотя бы одну клетку, содержащую единицу.
Для получения тупиковой ДНФ логической функции по карте Карно необходимо найти такую совокупность максимальных правильных контуров, у которых каждый контур охватывал хотя бы одну клетку, содержащую единицу, и не охваченную другими контурами, а совокупность контуров была полной, т.е. охватывала бы все единичные клетки карты Карно. Кроме того, необходимо выписать соответствующие им простые импликанты и объединить их знаком дизъюнкции.
При определении тупиковых ДНФ логических функций по картам Карно прежде всего должны быть определены максимальные правильные контуры, соответствующие существенным простым импликантам, составляющим ядро логической функции. Отличительным признаком такого контура является вхождение в него хотя бы одной единичной клетки, которая может быть охвачена только этим контуром. Так, из рис. 3.3, а видно, что существенным контуром представленной на карте Карно функции является контур, охватывающий в единственном числе единичную клетку, соответствующую набору 0100. Указанный контур соответствует простой импликанте ядра логической функции и должен входить во все тупиковые формы.
После выбора контуров, соответствующих ядру логической функции, для покрытия оставшихся единичных клеток вводятся дополнительные максимальные контуры до тех пор, пока совокупность контуров не станет полной. При этом необходимо соблюдать осторожность, проверяя после введения каждого нового контура выполнение правила, требующего, чтобы каждый из выделенных контуров охватывал хотя бы одну единичную клетку, не охваченную другими контурами.
Пример 3.6. Определим тупиковые ДНФ логической функции, заданной на карте Карно (рис. 3.3, а). На рис. 3.3,б,в показаны карты Карно, на которых выделены совокупности контуров, соответствующие двум различным тупиковым формам логической функции. Найдем соответствующие выделенным контурам простые импликанты и запишем две тупиковые формы данной логической функции:
 =
= 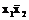
 ;
;
 =
= 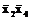

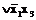 .
.
Тупиковая форма  содержит меньшее число переменных и является минимальной дизъюнктивной нормальной формой рассматриваемой логической функции.
содержит меньшее число переменных и является минимальной дизъюнктивной нормальной формой рассматриваемой логической функции.
| x4x3 | x2x1 | |||
| ~ | ||||
| ~ |
| x3x4 | x2x1 | |||
| ~ | ||||
| ~ |
| x4x3 | x2x1 | |||
| ~ | ||||
| ~ |
а б в
Рис. 3.3 Полные совокупности максимальных правильных контуров, соответствующих сокращенной (а), минимальной (б) и тупиковой (в) формам логической функции
С помощью карт Карно могут быть получены сокращенные и тупиковые конъюнктивные нормальные формы логических функций. Методика получения сокращенных и тупиковых КНФ полностью аналогична получению соответствующих дизъюнктивных форм и базируется на следующих основных положениях.
Правильный контур карты Карно, охватывающий одну клетку или группу клеток, соответствующих нулевым или нулевым и неопределенным значениям функции, и имеющий максимальный размер, соответствует простой имплиценте логической функции.
Правило записи имплицент логической функции аналогично определению конституент нуля логической функции по таблице соответствия или записи совершенной конъюнктивной формы функции. В элементарную дизъюнкцию, соответствующую имплиценте логической функции, включается переменная, если ее значения в клетках контура постоянны и равны нулю, и отрицание переменной, если ее значения постоянны и равны единице. Например, на рис. 3.4, а показаны двухклеточный и четырехклеточный максимальные правильные контуры, охватывающие нулевые и неопределенные клетки карты Карно.
| x4x3 | x2x1 | |||
| ~ | ||||
| ~ | ~ | |||
| ~ | ||||
| ~ |
| x3x4 | x2x1 | |||
| ~ | ||||
| ~ | ||||
| ~ | ||||
| ~ |
а б
Рис. 3.4. Совокупности максимальных правильных контуров, соответствующие
простым имплицентам  ,
, 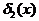 (а) и функции
(а) и функции  (б)
(б)
Соответствующие им простые импликанты имеют вид
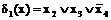 ;
;
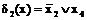 .
.
Сформулируем правило получения сокращенной и тупиковой конъюнктивных нормальной форм.
Для получения сокращенной КНФ логической функции по карте Карно необходимо найти все максимальные правильные контуры, охватывающие нулевые и неопределенные клетки, выписать соответствующие им простые имплиценты и объединить их знаком конъюнкции. При этом каждый из выделенных максимальных контуров должен охватывать хотя бы одну нулевую клетку.
Для получения тупиковой КНФ логической функции по карте Карно необходимо найти такую совокупность максимальных правильных контуров, у которых каждый контур этой совокупности охватывал хотя бы одну клетку, содержащую нуль, и не охваченную другими контурами, а совокупность контуров была полной, выписать соответствующие им простые имплиценты и объединить их знаком конъюнкции.
Пример 3.7. Определим тупиковую КНФ логической функции, заданной на карте Карно (рис. 3.1, б).
На рисунке показана карта Карно, на которой выделена совокупность контуров, соответствующая тупиковой КНФ логической функции. Определив соответствующие контурам имплиценты и объединив их знаком конъюнкции, получим
 =
=  .
.
Используя другие комбинации контуров для рассматриваемой логической функции, можно найти еще три тупиковые конъюнктивные нормальные формы.
 2017-11-30
2017-11-30 1943
1943
