Минимизация – процесс приведения булевых функций к такому виду, который допускает наиболее простую (с наименьшим числом элементов) физическую реализацию функции. Частная задача минимизации булевой функции сводится к такому представлению заданной функции, которое содержит наименьшее возможное число букв и наименьшее возможное число операций над ними, так как каждой элементарной логической функции соответствует определенный физический элемент.
Оценить различные представления одной и той же булевой функции, например ДНФ, можно по количеству входов логических элементов, реализующих заданную функцию. Такую оценку реализации булевой функции называют ценой реализации функции по Квайну (Мак-Класки) или ценой покрытия булевой функции системой логических элементов. Для минимизации переключательных функций применяют различные методы: последовательного исключения переменных с помощью законов алгебры логики, методом Квайна, карт Карно (Вейча) и др.
Метод последовательного исключения переменных с помощью законов и тождеств алгебры логики является наиболее простым методом минимизации. Любое упрощение переключательной функции происходит при вынесении за скобки общих множителей из минтермов, суммирование которых приводит к исключению отдельных переменных. Процесс подбора пары минтермов, сопровождающийся понижением ранга переменной, называется склеи ва нием минтермов.
В качестве примера рассмотрим минимизацию переключательной функции
F СДНФ = a 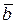
 Ú a b
Ú a b  Ú a b c
Ú a b c
методом последовательного исключения переменных. Сгруппируем первый минтерм со вторым, второй с третьим и проведем логические преобразования:
F = (a 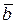
 Ú a b
Ú a b  )(a b
)(a b  Ú a b c) = a
Ú a b c) = a  (
(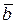 + b) Ú a b (
+ b) Ú a b ( + c) = a
+ c) = a  + a b.
+ a b.
Конъюнкции a  , a b входящие в такую сокращенную нормальную форму, называются импликантами.
, a b входящие в такую сокращенную нормальную форму, называются импликантами.
Простые импликанты – элементарные конъюнкции наименьшего ранга, входящие в данную булеву функцию.
Сокращенной дизъюнктивной нормальной формой булевой функции называется такая функция, которая равна дизъюнкции всех своих простых импликант. Несмотря на то, что сокращенная ДНФ булевой функции содержит меньшее число букв, чем СДНФ этой функции, она в большинстве случаев допускает упрощение за счет поглощения некоторых простых импликант дизъюнкцией других простых импликант. В случае, если в дизъюнкции простых импликант, представляющих заданную функцию, ни одну из импликант исключить нельзя, то такую дизъюнкцию называют тупиковой дизъюнктивной нормальной формой.
Выявление групп минтермов, отличающихся между собой комбинациями одних и тех же переменных, при большом числе переменных является задачей довольно сложной. Кроме того, некоторые минтермы могут входить одновременно в несколько групп и, следовательно, задача образования групп не может быть решена однозначно. Группируя минтермы различными способами, можно получить различные упрощенные формы заданной функции. Возможно, что получена одна из тупиковых форм, но нельзя быть уверенным, что она является минимальной.
Метод Квайна
Метод Квайна применяется для переключательных функций невысокого ранга при условии, что исходные функции заданы в СДНФ. Метод Квайна выполняется в два этапа: на первом этапе осуществляется переход от канонической формы СДНФ к сокращенной, на втором этапе – переход от сокращенной формы логического выражения к минимальной.
Пусть задана функция:
F СДНФ = 
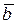
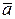 Ú
Ú 
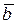 a Ú
a Ú  b
b 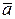 Ú с
Ú с 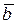 a Ú a b c
a Ú a b c
Составим следующие пары минтермов:
1 
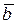
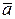 Ú
Ú 
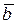 a =
a = 
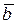 (
(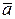 Ú a) =
Ú a) = 
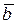
2 
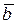
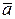 Ú
Ú  b
b 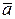 =
= 
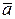 (
(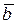
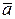 Ú b) =
Ú b) = 
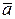
3 
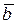 a Ú с
a Ú с 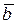 a =
a = 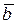 a (
a (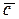 + с) =
+ с) = 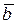 a
a
4 с 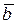 a Ú a b с = с a (
a Ú a b с = с a (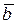 +b) = с a
+b) = с a
Сумма найденных импликант представляет сокращенную ДНФ исходной функции:
F ДНФ = 
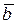 Ú
Ú 
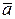 Ú
Ú 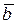 a Ú c a.
a Ú c a.
Каждой переключательной функции соответствует только одна нормальная форма, тогда как минимальных форм может быть несколькоМинимальная форма переключательной функции должна содержать все импликанты, перекрывающие все минтермы заданной функции. Для рассматриваемой функции можно получить две минимальные формы:
Fmin 1 = 
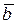 Ú
Ú 
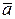 Ú c a и Fmin 2 =
Ú c a и Fmin 2 = 
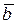 Ú
Ú 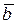
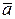 Ú c a,
Ú c a,
которые не совпадают с полученной ранее тупиковой формой. Проще всего это можно сделать методом карт Карно (Вейча).
Достоинством метода Квайна является четкость сформулированных правил проведения отдельных операций, благодаря чему возможно использование ЭВМ для минимизации достаточно сложных функций.
Минимизация логических функций по картам Карно
Метод минимизации по картам Карно (Вейча) находит широкое применение для минимизации переключательных функций 3 – 6 аргументов, поскольку обеспечивает простоту получения результата.
При использовании карт Карно (диаграмм Вейча) функцию предварительно следует привести к дизъюнктивной нормальной форме (ДНФ) – выразить в виде логической суммы простых конъюнкций (минтермов).
После этого формируется таблица (исходная, образцовая), количество клеток в которой равно числу минтермов 2m, где m – число переменных.
Пример 1. Минимизировать функцию
F = 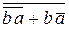 +
+ 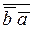 .
.
Приводим функцию к ДНФ, пользуясь правилами де Моргана:
F = 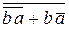 +
+ 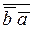 =
= 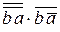 +
+ 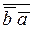 =
= 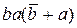 + (b+a) = ba + b + a =
+ (b+a) = ba + b + a =
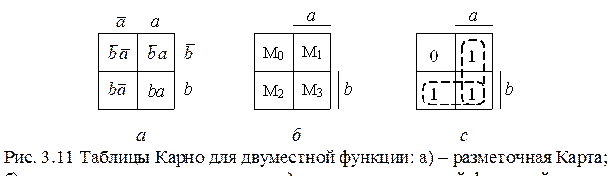 |
= b + a = b (a +
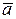 ) + a (b+
) + a (b+ 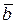 ) = ba + b
) = ba + b 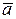 +
+ 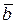 a.
a. На рис. 3.11, а, б, в приведены карты (таблицы) Карно для двух переменных. В табл. 3.11, а показана разметка карты. На карте 3.11, б в клетках карты указаны номера минтермов, расположенных в них. Принцип нумерации таков. Аргумент функции (крайний справа) имеет вес 20 = 1, старший аргумент (крайний слева) – вес 2 m -1. Минтерм М 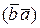 имеет нулевой номер, минтерм М(b, a) – номер три М3.
имеет нулевой номер, минтерм М(b, a) – номер три М3.
Для приведенного примера
F (b, a) = М3 + М2 + М1.
Нанесем на карту полученную функцию, записанную в СДНФ. В клетки 3–2–1 запишем единицы, а в нулевую клетку – ноль. Необходимо клетки с единицами обвести прямоугольными (квадратными) контурами и записать минимизированную функцию в виде суммы логических произведений, описывающих эти контура. Нетрудно заметить, что один контур описывается переменой а, а второй контур – b. Минимизированное выражение исходной функции будет следующим: F = b + a.
Пример 2. Минимизировать функцию трех аргументов (трехместную)
F = 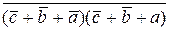 +
+ 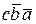 +
+ 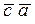 .
.
Приедем функцию к ДНФ:
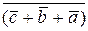 +
+ 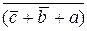 +
+ 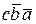 +
+ 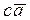 = c b a +
= c b a + 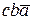 +
+ 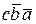 +
+ 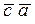 =
=
= c b a + 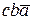 +
+ 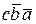 +
+ 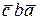 +
+ 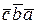 .
.
Запишем функцию в виде суммы минтермов:
F = М7 + М6 + М4 + М2 + М0.
На рис. 3.10 показаны две разметочные карты (табл 3.10 а, б), по которым можно понять принцип разметки.
Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбинации значений аргументов другой группы – строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующим последовательности чисел в коде Грея, поскольку в этом случае склеивающиеся клетки находятся рядом (любые две соседние клетки отличаются друг от друга только одним аргументом).
Нанесем ранее полученную функцию на карту (табл 3.10 в).
 |
Обведем клетки в которых расположены единицы контурами. Таких контуров получилось два. Запишем минимизированное выражение для исходной функции: F = с + 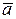 .
.
Пример 3. Минимизировать функцию четырех аргументов (четырех местную)
F = 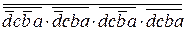 +
+ 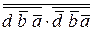 +
+ 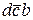 +
+ 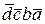 .
.
Приведем функцию к ДНФ, пользуясь правилом отрицания:
F = 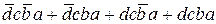 +
+ 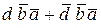 +
+ 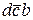 +
+ 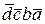 .
.
Преобразуем функцию к СДНФ
F = 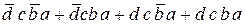 +
+ 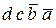 +
+ 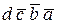 +
+ 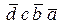 +
+ 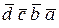 + +
+ + 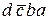 +
+ 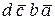 +
+ 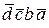 .
.
Запишем выражение в виде суммы минтермов
F = М5 + М7 + М13 + М15 + М12 + М8 + М4 + М0 + М11 + М10 + М2.
На рис. 3.11 а, б представлена разметочная карта для четырехместной функции (табл 3.11 а). В клеточках карты указаны номера минтермов, помещающихся в эти клетки. Разместим функцию на такую карту: впишем единицы в те клеточки, номера которых имеются в полученном выражении.
Карта с нанесенной на нее функцией приведена на рис. 3. 11 (табл. б).
 |
Обведем клетки с единицами контурами и опишем их суммой конъюнкций. Миниизированное выражение для исходной функции
F = 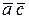 +
+ 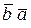 +
+ 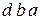 .
.
Выводы
Карта Карно определяет значение функции на всех возможных наборах аргументов и, следовательно, является таблицей истинности. Карты Карно компактны и удобны для поиска склеиваемых членов переключательной функции СДНФ. Объясняется это тем, что два любых минтерма, находящихся в клетках, расположенных рядом друг с другом, являются соседними. Они могут быть заменены одной конъюнкцией, содержащей на одну переменную меньше. Группа из четырех минтермов, расположенных в соседних клетках, может быть заменена конъюнкцией, содержащей на две переменные меньше. В общем случае группа из 2 k соседних клеток будет заменена одной конъюнкцией с n – k аргументами, при общем числе переменных равным n.
Минимизацию переключательных функций будем вести на основании следующих правил:
♦ все клетки, содержащие 1, объединяются в замкнутые области;
♦ каждая область должна представлять собой прямоугольник или квадрат с числом клеток 2 k;
♦ клетки, расположенные на противоположных гранях таблицы, являются соседними, так как карту можно сворачивать в цилиндр по горизонтали и по вертикали;
♦ угловые клетки, расположенные на противоположных углах, являются соседними, в том числе все четыре угловые клетки объединяются в одну область;
♦ области могут пересекаться, одни и те же клетки могут входить в разные области;
♦ клетки, значение функции в которых не определено (Ф), могут принимать любое значение (0 или 1);
♦ необходимо стремиться к тому, чтобы число областей было минимальным, а каждая область содержала возможно большее число клеток.
Пример 3. Минимизировать функцию пяти аргументов (пятиместную).
Карту Карно пяти аргументов создадим следующим образом. Перевернем четырехместную карту вокруг правой стороны (можно вращать вокруг нижней стороны). Разметку оставляем прежней (d c b a), лишь по строкам правой половине присваиваем имя старшего разряда (е d c b a).
Разметочная карта (таблица, диаграмма), с нанесенными номерами минтермов расположена на рис. 3.11 а.
Функция задана в виде суммы минтермов и нескольких минтермов – функционалов, способных принимать значение 1 или 0.
F = М0 + М2 + М4 + М5 + М7 + Ф8 + Ф9 + М10 + М12 + М13 + Ф15+ М16 + Ф17 + М18 + М20 + М21 + М23 + Ф24 + М26 + М28 + Ф29 + Ф30+ М31.
 |
Заполним карту Карно для данной функции (рис. 3.11, б). Проведем контура, охватывающие единицы. Контур может содержать функционалы, поскольку тогда их значение по умолчанию равно единице. Потребовалось всего три контура для описания всех единиц. Запишем минимизированное выражение для этой функции:
Fмин = 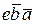 + ca +
+ ca + 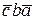 .
.
Во входной функции находилось 16×5 = 80 букв (переменных), а в минимизированной всего восемь, имеем 10-кратный выигрыш, что конечно впечатляет.
|
 2015-03-22
2015-03-22 3528
3528