Положительные числовые ряды. Интегральный признак сходимости. Интегральная оценка суммы ряда.
Из МатАнализа:
Монотонно возрастающая и ограниченная СВЕРХУ функция имеет предел:
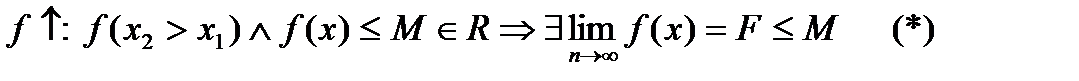
Рассмотрим положительную числовую последовательность 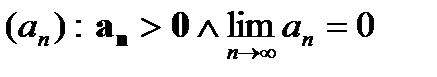 , положительную числовую функцию a(x): a(x=n∊N)=an и соответствующие им числовой ряд
, положительную числовую функцию a(x): a(x=n∊N)=an и соответствующие им числовой ряд 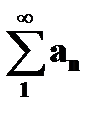 и несобственный интеграл
и несобственный интеграл 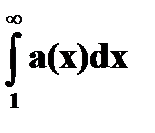 :
:
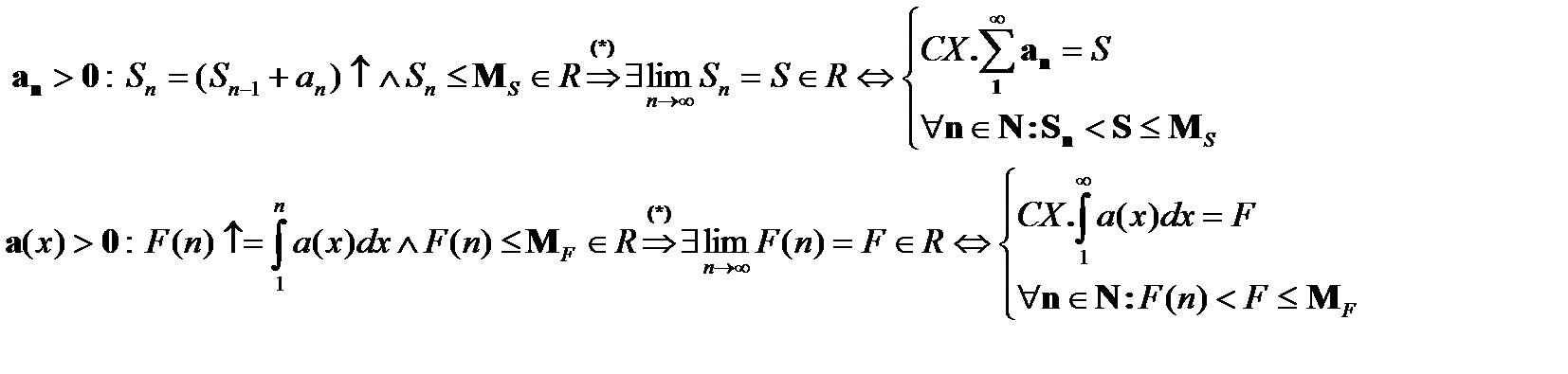
Теорема (интегральный признак сходимости/расходимости положительного ряда).
«Положительный числовой ряд 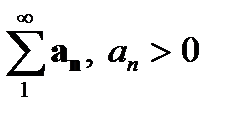 :
:
(1) сходится и расходится одновременно с несобственным интегралом 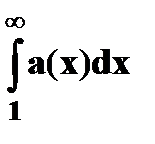 ,
,
(2) для сходящегося ряда 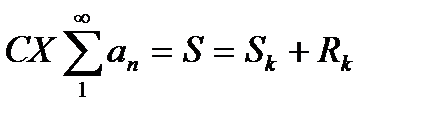 имеют место
имеют место
- «интегральная оценка» суммы его остатка 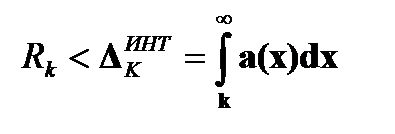 и
и
- «интегральная оценка» суммы ряда 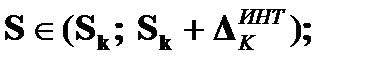
Док-во теоремы следует из сравнения на промежутках [1;n] и [n;∞) площадей криволинейной трапеции SKT, ограниченной сверху линией у=а(х), n ≥ х ≥ 1, вписанной SВП и описанной SОП ступенчатых фигур, образованных прямоугольниками высотой aК и шириной ∆х = 1:
[1;n]: SОП = a1+a2+..+an-1 = Sn-1 > 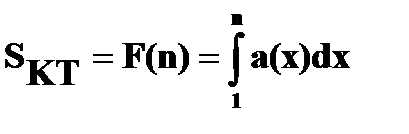 > SВП = a2+a3+..an = Sn - a1, (1)
> SВП = a2+a3+..an = Sn - a1, (1)
[n;∞): 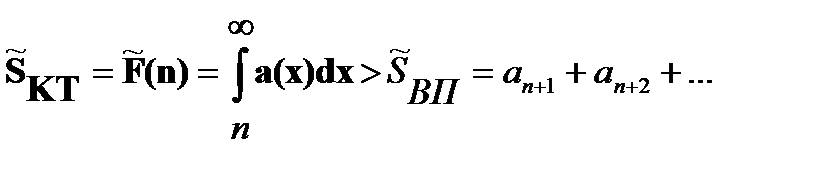 (2)
(2)
| an-1 |
| a1 |
| x |
| an+1 |
| an |
| a2 |
| a(x) |
| n+1 |
| n-1 |
| n |
Из монотонного возрастания функций Sn↑ и F(n) и неравенств (1) 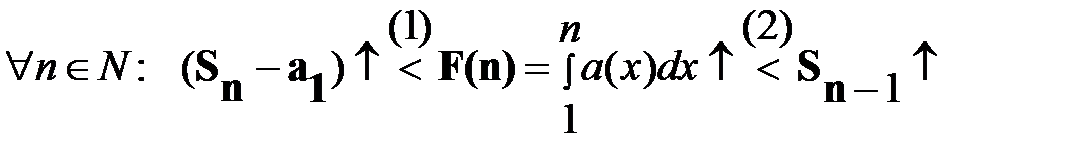 следует:
следует:
[1].
(а) если несобственный интеграл сходится 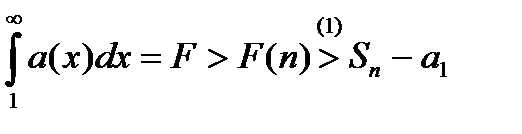 , то
, то 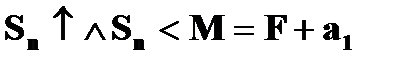
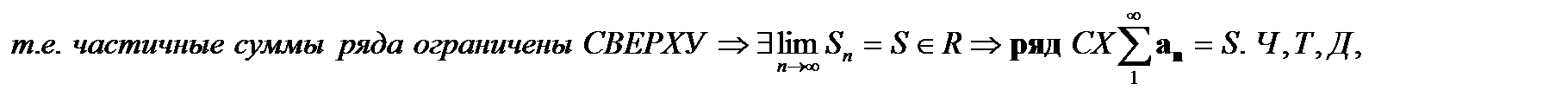
б) если же интеграл расходится 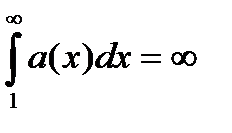 , то
, то
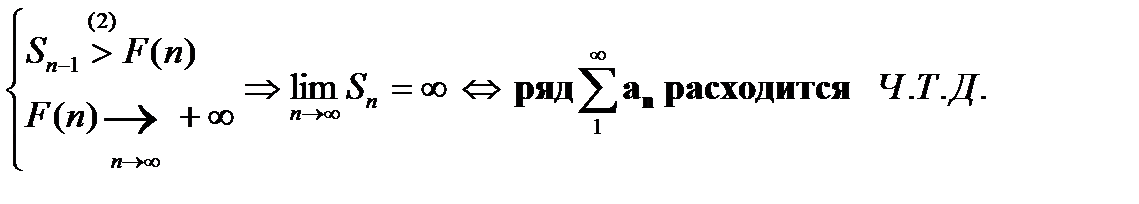
[2]. Пусть ряд сходится: 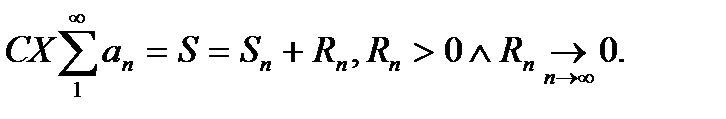 Тогда из неравенств (2) следует:
Тогда из неравенств (2) следует:
- 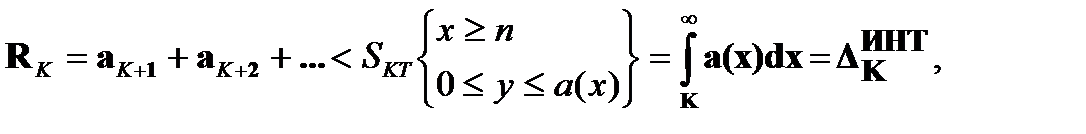 - «интегральная оценка СВЕРХУ суммы остатка положительного ряда» и
- «интегральная оценка СВЕРХУ суммы остатка положительного ряда» и
- 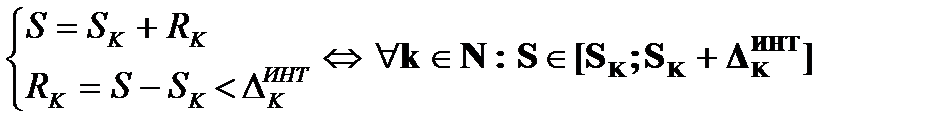 - «интегральная оценка суммы ряда».
- «интегральная оценка суммы ряда».
Признаки сравнения положительных числовых рядов.
Пусть 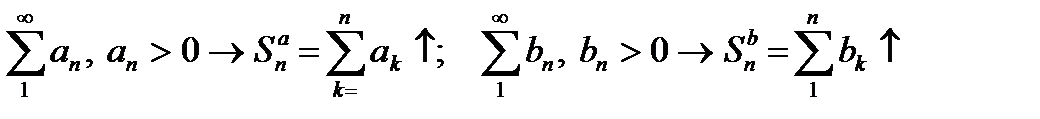
Если 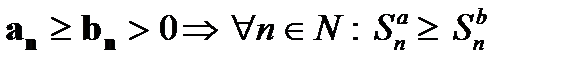 ; при сравнении рядов используют символ мажорирования
; при сравнении рядов используют символ мажорирования
«>>» и пишут 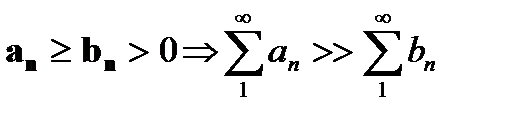
Теорема1 (признак сравнения ). Если 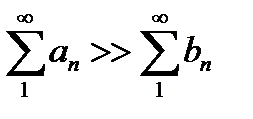 , то:
, то:
(1) из сходимости мажорирующего(«б’ольшего») ряда 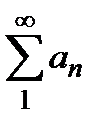 следует сходимость ряда
следует сходимость ряда 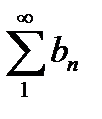 и
и
(2) из расходимости мажорируемого(«меньшего») ряда 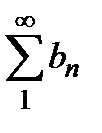 следует расходимость ряда
следует расходимость ряда 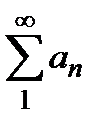 .
.
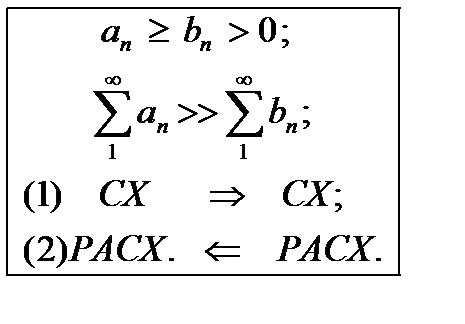
Док-во.
(1) Пусть ряд 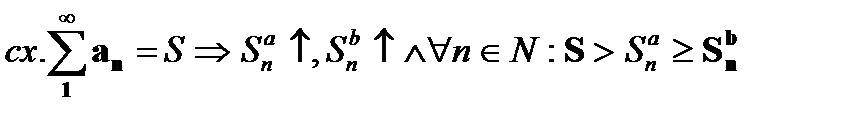 ,
, 
(2) Если ряд 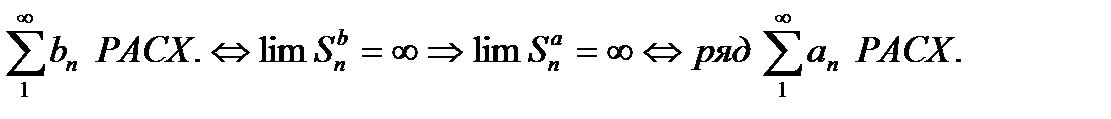 ч.т.д.
ч.т.д.
Пример. 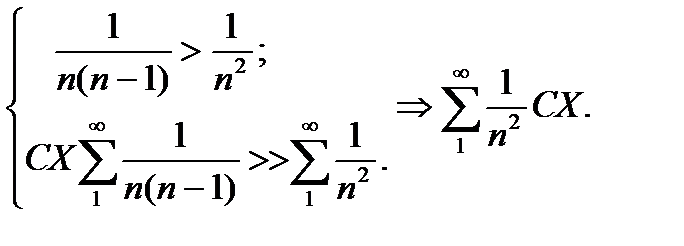
Признак 2 (предельный признак сравнения).
Если существует конечный предел отношения членов положительных рядов
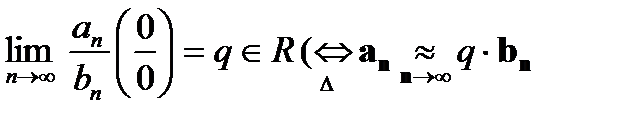 - равносильные б. малые при n→∞),
- равносильные б. малые при n→∞),
ряды 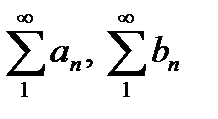 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
Доказательство следует из определения предела числовой последовательности и признака сравнения 1.
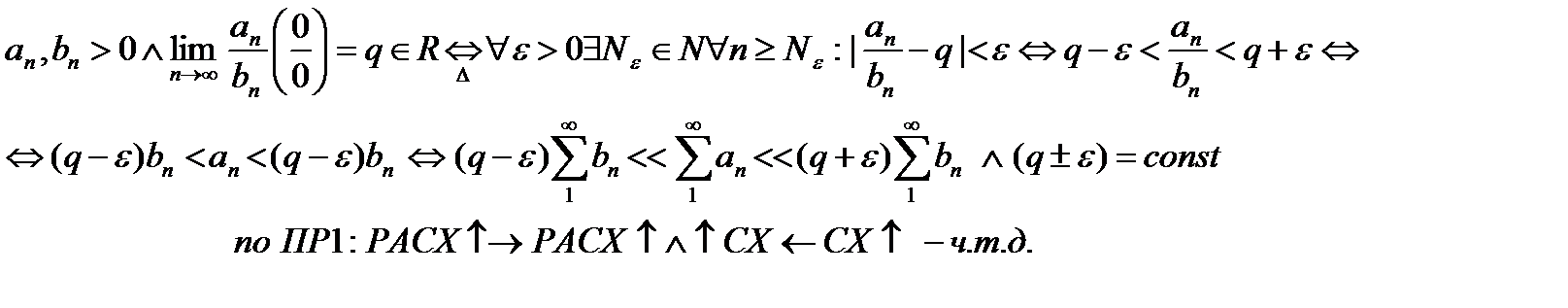
------------------------------------------------------------------------
Замечания.
1) Предельный признак сравнения и интегральный признак являются основным «инструментом» исследования сходимости и расходимости положительных рядов, общий член которых содержит только степенные функции: 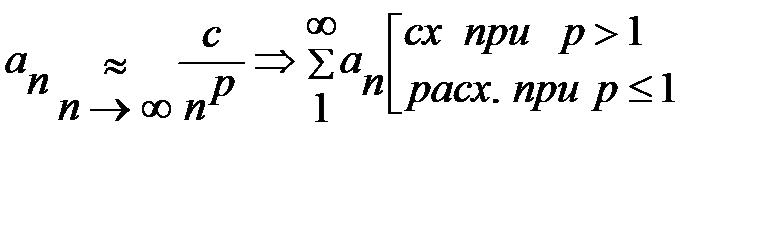 ;
;
2) Для установления отношения равносильности 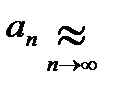 из суммы слагаемых рекомендуется вынести слагаемое с наибольшей степенью “nmax”.
из суммы слагаемых рекомендуется вынести слагаемое с наибольшей степенью “nmax”.
3) При получении интегральной оценки суммы остатка ряда подынтегральную функцию можно
«преувеличить»: 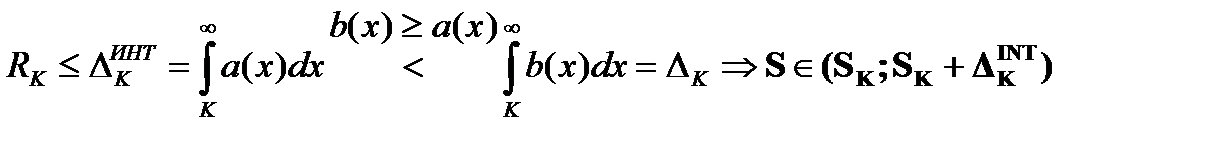
например, увеличив числитель или уменьшив знаменатель дроби.
4) SK округляется «по недостатку», а 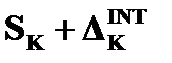 - «по избытку».
- «по избытку».
ПРИМЕР Доказать сходимость и найти оценку суммы ряда с погрешностью eps=0.001
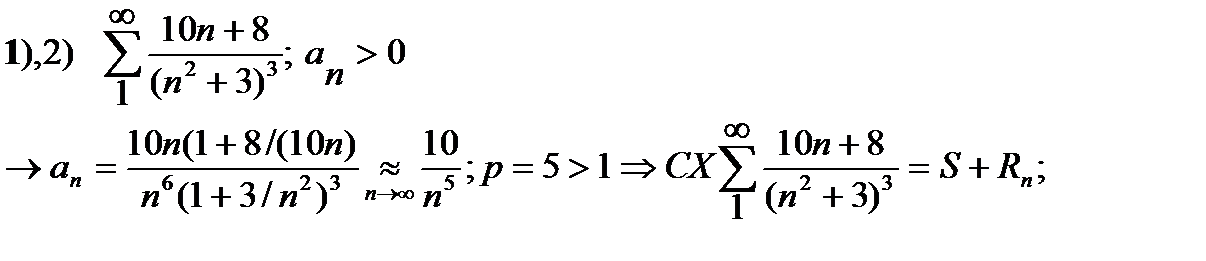
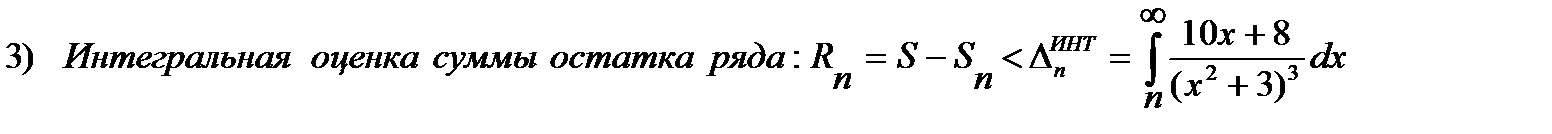
Интеграл можно вычислить точно (см. Двайт 120.2). Для упрощения вычислений преувеличим оценку 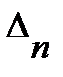 , увеличив числитель или уменьшивзнаменатель дроби:
, увеличив числитель или уменьшивзнаменатель дроби: 
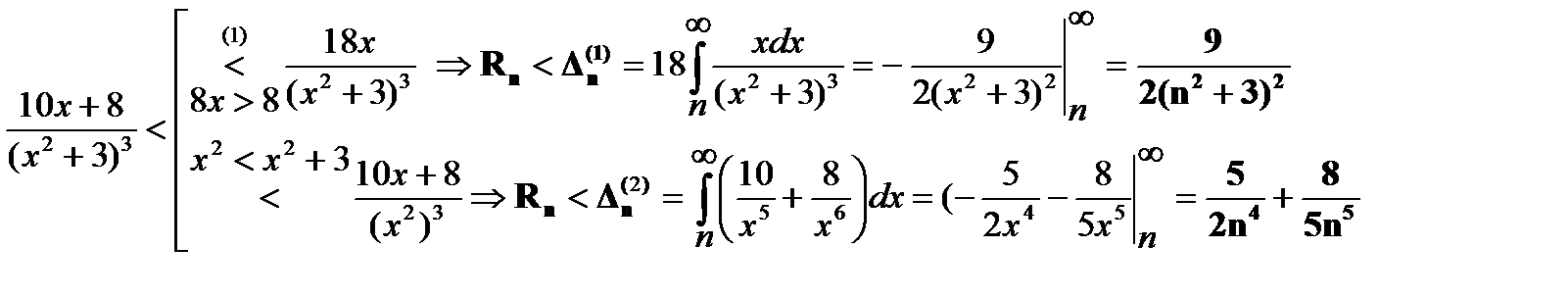
Оценку с погрешностью «eps=0.001» получим, решив неравенство 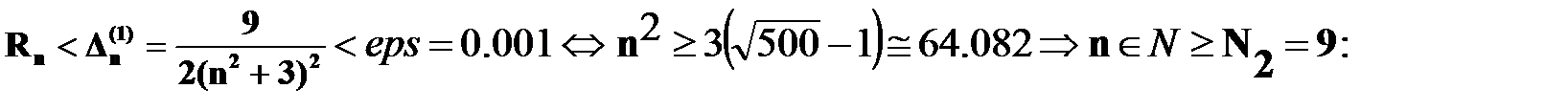
1.3 Оценка суммы ряда 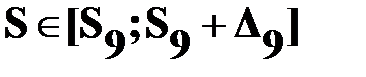
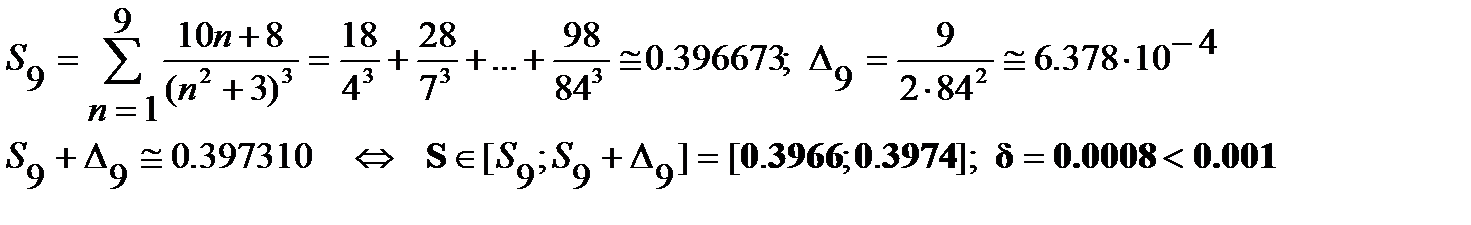
Результат: 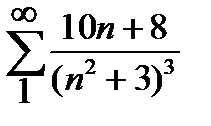 =
= 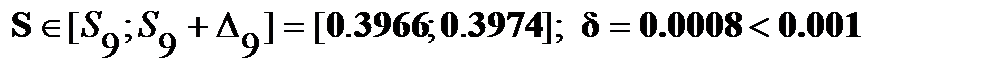
 2017-11-30
2017-11-30 490
490






