Цилиндр бесконечной длины

Рассмотрим охлаждение равномерно прогретого круглого цилиндра большой длины радиусом r в среде с меньшей постоянной температурой. Коэффициент теплоотдачи от поверхности цилиндра к среде не меняется во времени. Физические величины с, ρ и λ материала цилиндра не зависят от температуры и считаются известными. Необходимо определить: температуру поверхности, температуру на оси цилиндра и количество тепла, отданное цилиндром в окружающую среду, для любого момента времени.

Для цилиндра неограниченной длины дифференциальное уравнение теплопроводности удобнее отнести к цилиндрическим координатам. Примем, что в начальный момент времени (τ = 0) температура по всему объему цилиндра постоянна. Тогда

(4-9)

Задача на охлаждение цилиндра аналогична задаче охлаждения пластины. Поэтому значения температуры на поверхности, на центральной оси и тепловые потери цилиндра через произвольные промежутки времени определяются из следующих соотношений:

= f(Bi, Fo), = f₁(Bi, Fo), = f₂(Bi, Fo). (4-10)

Для цилиндрической стенки

Bi = ; Fo = ,

где r — радиус цилиндра.

Величины , и для найденных значений Bi, Fo определяют по таблицам, затем по найденным табличным значениям определяют абсолютные значения t _cт , t _ц и Q _τ.

Внутреннюю энергию рассматриваемого участка цилиндра длиной l, отсчитанную от ее значения при температуре среды как от нуля, находим по формуле

Q ₀ = π r ² lρсQ ₁ Дж.

Шар.

Рассмотрим охлаждение шара радиусом r, масса которого равномерно прогрета до постоянной температуры, в среде с более низкой постоянной температурой. Физические постоянные с, ρ и λ материала шара, а также коэффициент теплоотдачи считаем известными. Требуется определить для любого момента времени значения: температуры поверхности, температуры в центре шара и количества тепла, теряемого шаром в окружающую среду.

Дифференциальное уравнение теплопроводности удобнее отнести к сферическим координатам:

. (4-12)

Задача на охлаждение шара аналогична задачам на охлаждение пластины и цилиндра; безразмерные величины , и 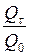являются функциями только критериев Bi и Fo и определяются из следующих соотношений:

= f(Bi, Fo), = f₁(Bi, Fo), = f₂(Bi, Fo).

Для шара

Bi = ; Fo = ,

где r — радиус шара.

Зависимости между безразмерными величинами определяются по таблицам нестационарного теплообмена для шара, а затем по этим зависимостям определяются абсолютные значения t _cт t _ц и Q _τ.

Начальная внутренняя энергия шара отсчитывается от ее значения при температуре среды, как от нуля, по формуле

Q ₀ = 4/3 π r ³ ρc (t ₀ - t _cp.). (4-13)

Регулярный режим.

Охлаждение во времени однородного изотропного тела произвольной формы в среде с постоянной температурой и постоянным коэффициентом теплоотдачи на его поверхности определяется дифференциальным уравнением теплопроводности:

(4-14)

и граничными условиями

, t (τ = 0) = f(x, y, z).

Решение уравнения (4-14) при t _ср = const показывает, что температура в любой точке тела изменяется по экспоненциальному закону:

, (4-15)

где Q = t ₀ - t _ср;

А _i — постоянные, зависящие от формы тела и начального распределения температур;

U _i — функции координат, характеризующие изменение температуры в пространстве;

m _i — постоянные, представляющие собой ряд положительных возрастающих чисел { m ₁ < m ₂ < m ₃ <...< m _i).

Анализ уравнения (4-15) показывает, что при малых значениях τ от τ = 0 до τ = τ ₁ процесс охлаждения (нагревания) зависит от начальных условий охлаждения и имеет случайный характер, не связанный с условиями охлаждения. Этот период охлаждения будет определяться не только первым членом, но и последующими членами ряда (4-15). Эту стадию охлаждения называют первым периодом охлаждения, или неупорядоченным процессом.

С увеличением времени τ ряд быстро сходится и все члены его, кроме первого, стремятся к нулю. При значении τ, превышающем некоторое определенное значение τ > τ ₁, начальные условия начинают играть второстепенную роль и процесс полностью определяется условиями охлаждения на поверхности тела, физическими свойствами, геометрической формой и размерами тела. Вторая стадия охлаждения называется регулярным режимом и описывается первым членом ряда (4-15), т. е.

. (4-16)

Логарифмируя последнее уравнение, имеем

ln = ln (AU) – mτ = – mτ + C (x, y, z). (4-17)

Из уравнения (4-17) видно, что регулярный режим характеризуется тем, что натуральный логарифм избыточной температуры любой точки тела изменяется во времени по линейному закону.

После дифференцирования обеих частей уравнения (4-17) по времени получаем

(с)^-1. (4-18)

Относительная скорость изменения температуры в единицу времени в любой точке тела не зависит от координат и времени. Величину т называют темпом охлаждения и определяют из опыта. Если взять внутри тела какую-либо точку и измерять в этой точке температуру, то процесс охлаждения можно представить кривой q = f(τ) (рис. 4-2). Величина τ, очевидно, равна тангенсу угла наклона прямолинейного участка характеристики к оси абсцисс:

. (4-19)

Рис. 4-2.

Теория регулярного режима, разработанная Г. М. Кондратьевым, применима к телам любой формы. Она позволила установить связь между темпом охлаждения тела, его физическими и геометрическими величинами и внешними условиями теплообмена. В общем случае величина т оценивается из уравнения

, (4-20)

т. е. величина т, характеризующая скорость охлаждения тела, прямо пропорциональна коэффициенту теплоотдачи a (если a не → ∞), поверхности тела F и обратно пропорциональна его полной теплоемкости С = cρV; Ψ - безразмерный коэффициент пропорциональности, характеризующий неравномерность распределения температуры в теле и являющийся функцией критерия Био.

Это уравнение выражает закон сохранения энергии для охлаждающегося тела в среде с постоянной температурой. Если Ψ = 1, то распределение температур в теле равномерное; если Ψ = 0, то распределение температур становится наиболее неравномерным - температура поверхности равна температуре среды, а температура внутри всего тела не равна температуре поверхности.

Если коэффициент теплоотдачи a → ∞, то величина т прямо пропорциональна коэффициенту температуропроводности охлаждающегося тела:

m _∞ = a / K или a = K m _∞ м²/с, (4-21)

где К — коэффициент пропорциональности, зависящий от геометрических размеров и формы тела.

 

 

К следующему занятию курсанты должны:

ЗНАТЬ: методы решения уравнения теплопроводности при нестационарном тепловом режиме.

УМЕТЬ: решать уравнение теплопроводности через стенки различной формы при различных значениях критериев Био и Фурье.

ИМЕТЬ ПРЕДСТАВЛЕНИЕ: о взаимосвязи между темпом охлаждения (нагревания) тела, его физическими и геометрическими параметрами и внешними условиями теплообмена.

 

 

Вопросы на самоподготовку:

1. Что называется нестационарным температурным полем?

2. Дифференциальное уравнение теплопроводности и граничные условия для нестационарного режима.

3. Уравнение температурного поля для нестационарного режима.

4. Из каких критериев подобия составляется уравнение температурного поля?

5. Методика определения температуры поверхности пластины (цилиндра, шара), температуры в середине пластины и количества теплоты, отводимого при охлаждении пластины (цилиндра, шара).

6. Какими дифференциальными уравнениями описывается охлаждение однородного, изотропного и равномерно нагретого тела произвольной формы, имеющего начальную постоянную температуру?

7. На какие два периода можно разделить охлаждение тела с постоянной начальной температурой?

8. Что такое темп охлаждения и от значений каких переменных он зависит?

 

 

Подпись автора

___________/ профессор каф. физики и теплообмена П.В. Скрипов

 

 

Лекция рассмотрена и одобрена на заседании кафедры

Протокол №_______ от «_____»_____________2006 г.

 

Зав. кафедрой физики и теплообмена

профессор, д.т.н. __________________ / Н.М. Барбин

«_____»______________ 2006 г.