Особенности практического применения

Линейных множественных регрессионных моделей

Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т. е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы ис­ходных данных линейно независимы. Для экономических показате­лей это условие выполняется не всегда.

Под мультиколлинеарностью понимается высокая взаимнаякоррелированность объясняющих переменных (факторов), которая приводит к линейной зависимости нормальных уравнений. Существует несколько способов для определения наличия или отсутствия мультиколлинеарности.Один из подходов заключается в анализе коэффициентов парной корреляции.

1. Факторные признаки, у которых 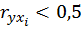исключают из модели.

2. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными (факторами) больше 0,8. В этом случае одну переменную исключают из рассмотрения. При этом какую пе­ременную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с эконо­мической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.

 

Пример 2.9. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах проведены измерения уровня месячной зарплаты X и числа уволившихся за год рабочих Y:

X
Y

 

Найти линейную регрессию Y на X. Провести статистический анализ.

Решение

На рис.2.19 решена задача простой линейной регрессии. Для нахождения коэффициентов линейной регрессии использованы встроенные функции slope, intercept. Проведен сравнительный визуальный анализ расположения экспериментальных точек и полученной функциональной зависимости.

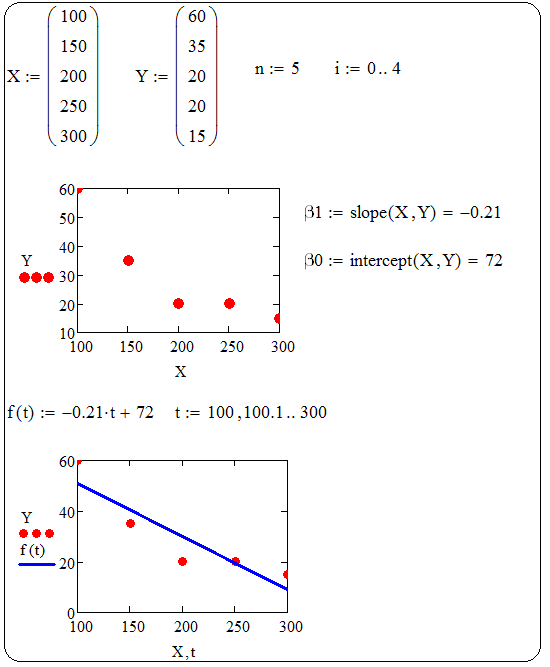
Рис. 2.19 Однофакторная линейная регрессия

 

Проведем статистический анализ (рис. 2.20).

1. Коэффициент корреляции равен (-0,904), следовательно, связь тесная и обратная. Коэффициент корреляции значим, т.е. зарплата оказывает существенное влияние на текучесть рабочей силы.

2. Полученное уравнение регрессии является значимым, т.е. для описания зависимой переменной достаточно одного фактора.

3. Коэффициент эластичности равен (-1,4), т.е. при увеличении зарплаты на 1% текучесть рабочей силы уменьшается в среднем на 1,4%.

4. Коэффициент детерминации равен 0,817, т.е. на 81,7% текучесть рабочей силы зависит от заработной платы и на 18,3% от других неучтенных факторов.

5. Ошибка аппроксимации составляет 24,6%. Следовательно, полученную функциональную зависимость не следует использовать для прогнозирования. Рекомендуется подобрать другую однофакторную модель регрессии (нелинейную).

Рис. 2.20. Статистический анализ

Пример 2.10. Имеются следующие данные о сменной добыче угля на одного рабочего Y (т), мощности пласта X 1(м) и уровне механизации работ X2 (%), характеризующие процесс добычи угля в 10 шахтах. Предполагая, что между переменными Y, X 1 и X 2существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y по X 1 и X 2 ). Провести статистический анализ.

Решение

1.Матрицу А формируем объединением столбцов с элементами 1, Х 1, Х 2 с применением встроенной функции augment. По алгоритму получаем оценки параметров β, что позволяет составить уравнение двухфакторной линейной регрессии. Ошибка аппроксимации составляет 10,24%, что позволяет использовать полученное уравнение в прогностических целях.

Рис. 2.21. Вариант двухфакторной линейной регрессии

Уравнение множественной регрессии показывает, что при увеличении только мощности пласта Х 1 (при неизменном Х 2) на 1 м, добыча угля на одного рабочего увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ Х 2 (при неизменном Х 1) – в среднем на 0,367 т.

2. Проведем сравнение раздельного влияния на добычу угля двух факторов – мощности пласта Х 1 и уровня механизации работ Х 2. Для этого вычислим коэффициенты эластичности.

 

Рис. 2.22. Коэффициенты эластичности

Увеличение факторов на 1% (от своих средних значений) приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. Таким образом, на добычу угля большее влияние оказывает фактор Х 1 (мощность пласта) по сравнению с фактором Х 2 (уровень механизации).

3. Определим множественный коэффициент корреляции и проверим его значимость и значимость полученного уравнения регрессии.

Рис. 2.23.Вычисление множественного коэффициента

корреляции

Значение 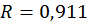, близкое к 1, указывает на тесную взаимосвязь переменной Y и факторов Х 1 и Х 2. Коэффициент детерминации 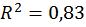свидетельствует о том, что вариация исследуемой зависимой переменной на 83% объясняется изменчивостью включенных в модель факторов.

Проверим значимость коэффициента корреляции. Наблюдаемое значение tN принадлежит критической области, следовательно, гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности отвергаем.

Проверим значимость уравнения регрессии. Наблюдаемое значение FN принадлежит критической области, следовательно, гипотезу «уравнение регрессии ненадежно» отвергаем.

4. Мультиколлинеарность.

Рис. 2.24. Парные коэффициенты корреляции

Так как 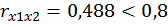, то явление мультиколлинеарности не установлено; 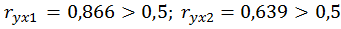, следовательно, факторы не исключаются из модели.