| Регрессии, нелинейные относительно включенных факторов, но линейные по оцениваемым параметрам | Регрессии, нелинейные по оцениваемы параметрам |
Полиномы разных степеней, например,   . Заменяя переменные, например, . Заменяя переменные, например,  , получим уравнение множественной линейной регрессии. , получим уравнение множественной линейной регрессии. | 1.Внутренне линейные, например, функции: степенная  показательная показательная 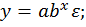 экспоненциальная экспоненциальная 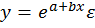 . С помощью соответствующих преобразований приводятся к простой линейной регрессии. 2. Внутренне нелинейные, например, функции: . С помощью соответствующих преобразований приводятся к простой линейной регрессии. 2. Внутренне нелинейные, например, функции:   Используют итеративные процедуры. Используют итеративные процедуры. |
Пример 2.11. В контрольный период проведено 10 измерений некоторой величины. Измерения проводились через фиксированный интервал времени. Результаты наблюдений Y сведены в таблицу. Решить задачу регрессии, используя в качестве зависимостей полиномы с 1 по 5 степеней. Сопоставить точности вариантов.
| № | ||||||||||
| Y | -0,72 | -0,637 | -0,031 | 0,533 | 1,269 | 3,537 | 5,158 | 7,499 | 10,62 | 12,531 |
Решение
На рис. 2.25 приведены результаты решения в среде MathCAD. Решения для полиномов разных степеней проведены по одному алгоритму.

Рис. 2.25. Варианты регрессии
Для сопоставления полиномиальных регрессионных выражения (от полинома первого порядка до пятого порядка включительно) вычислены остаточные суммы квадратов, которые обозначены Δ (рис. 2.26). Проведенные вычисления подтверждают качественную зависимость остаточной суммы от порядка полинома.

Рис. 2.26. Сопоставление полиномиальных регрессий
При выборе регрессионной модели путем сопоставления остаточных сумм квадратов (при условии их близких значений) выбирают более простой вариант модели. В качестве дополнительного упрощения выбранной регрессионной модели применяется функция чувствительности  , с помощью которой определяют вклад оценки каждого параметра в результирующее значение.
, с помощью которой определяют вклад оценки каждого параметра в результирующее значение.
Функция чувствительности f представляет собой m -мерный вектор-столбец. Умножая вектор f слева на диагональную матрицу N, элементы диагонали которой составляют вектор  , получаем вектор относительных функций чувствительности
, получаем вектор относительных функций чувствительности 
Пусть выбранная регрессионная модель – полином второго порядка  . На рис. 2.27 получен вектор относительной чувствительности для полинома второго порядка.
. На рис. 2.27 получен вектор относительной чувствительности для полинома второго порядка.

Рис. 2.27. Получение вектора относительной чувствительности
Анализ вектора F показывает, что наименьшая функция чувствительности у коэффициента  , следовательно, возможно применить упрощенную регрессионную модель
, следовательно, возможно применить упрощенную регрессионную модель  .
.

Рис. 2.28. Решение упрощенной задачи регрессии
Значение остаточной суммы квадратов, равное 0,948, незначительно отличается от значения 0,911. Таким образом, выбранная регрессионная модель имеет вид  .
.
 2017-12-14
2017-12-14 1039
1039
