Основные методы вероятностного расчета строительных конструкций
При проектировании строительных конструкций представляется весьма важным установить соответствие расчетной модели действительной работе конструкций в эксплуатации и правильно учитывать изменчивость случайных факторов. Расчет начинается с анализа структурной схемы сооружения и распределений несущей способности и внешних воздействий. Отсутствие отказов характеризуется тем, что усилия от нагрузок F не превышают несущую способность Ф, т. е. Ф-F>0 и Ф/F>1
В силу случайной природы прочности и нагрузок эти условия не могут быть выполнены абсолютно точно; оно соблюдается с некоторой вероятностью, достаточно близкой к единице, в течение срока службы сооружения. По мере развития теории надежности предлагались различные методы расчета надежности строительных конструкций.
Метод А.Р. Ржаницына
По методу А.Р. Ржаницына [5] условие недопустимости достижения опасного состояния конструкции и основания представляется в форме (рис. 22.1)
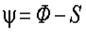
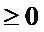 (22.1)
(22.1)
где 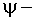 функция неразрушимости.
функция неразрушимости.
Функция неразрушимости зависит от многих случайных параметров 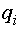 , и возникающие трудности построения кривых распределений нагрузки и несущей способности (прочности) преодолеваются тем, что эти кривые распределения принимаются за нормальные или логнормальные.
, и возникающие трудности построения кривых распределений нагрузки и несущей способности (прочности) преодолеваются тем, что эти кривые распределения принимаются за нормальные или логнормальные.
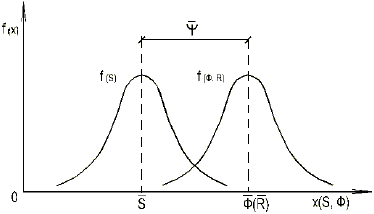
Рис. 22.1. Плотности распределения 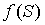 и
и 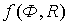
Если 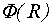 и
и 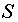 распределены по нормальному закону, функция распределения плотности вероятностей
распределены по нормальному закону, функция распределения плотности вероятностей 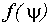 имеет вид:
имеет вид:
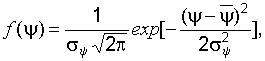 (22.2)
(22.2)
где 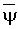 и
и 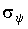 – математическое ожидание и стандарт для
– математическое ожидание и стандарт для 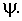
При этом
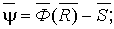 (22.3)
(22.3) 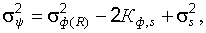 (22.4)
(22.4)
где 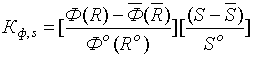 – коэффициент корреляции;
– коэффициент корреляции; 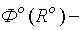 центрированная случайная величина
центрированная случайная величина 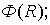
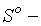 центрированная случайная величина
центрированная случайная величина 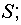
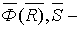 математическое ожидание для
математическое ожидание для  и
и 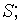
 ,
, 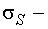 стандарт для
стандарт для  и
и 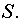
Если 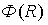 и
и 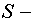 независимые случайные величины, то
независимые случайные величины, то
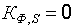 и
и 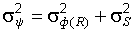 . (22.5)
. (22.5)
Надежность конструкции и основания по прочности определяется характеристикой безопасности 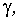 которая является обратной величиной по отношению к коэффициенту изменчивости распределения
которая является обратной величиной по отношению к коэффициенту изменчивости распределения 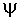 :
:
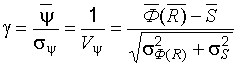 , (22.6)
, (22.6)
где 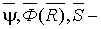 математические ожидания соответствующих распределений;
математические ожидания соответствующих распределений; 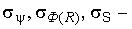 стандарты распределений;
стандарты распределений; 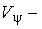 коэффициент вариации (изменчивости) для распределения
коэффициент вариации (изменчивости) для распределения 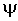 .
.
Определив 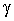 , можно оценить вероятность отказа Q или Р(+) безотказной работы конструкции и основания с помощью выражений:
, можно оценить вероятность отказа Q или Р(+) безотказной работы конструкции и основания с помощью выражений:
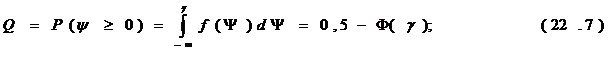 Р(+)=1- Q = 0,5 +Ф(
Р(+)=1- Q = 0,5 +Ф(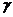 ). (22.7)
). (22.7)
Здесь 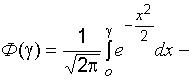 функция Лапласа, значения которой табулированы. При этом необходимо учитывать, что
функция Лапласа, значения которой табулированы. При этом необходимо учитывать, что 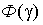 – нечетная функция, для которой
– нечетная функция, для которой 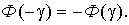
Между характеристикой безопасности 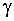 и надежностью конструкции и основания
и надежностью конструкции и основания 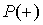 существует зависимость: чем больше величина
существует зависимость: чем больше величина 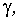 тем выше надежность. Например, при
тем выше надежность. Например, при 
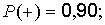 при
при 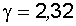
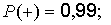 при
при 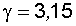
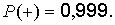
Математическое ожидание и стандарт величины 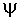 определяются на основании нормативных (средних) значений нагрузок и прочности материала конструкций и грунта основания, коэффициентов вариации
определяются на основании нормативных (средних) значений нагрузок и прочности материала конструкций и грунта основания, коэффициентов вариации 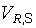 , необходимых для определения
, необходимых для определения 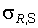 по условиям
по условиям 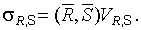
При логарифмически нормальном законе распределения 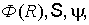 когда
когда 

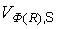 > 0,15- 0,20 характеристика безопасности определяется с помощью выражения
> 0,15- 0,20 характеристика безопасности определяется с помощью выражения
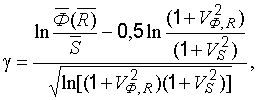 (22.8)
(22.8)
где 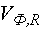 ,
, 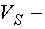 коэффициенты вариации соответствующих распределений.
коэффициенты вариации соответствующих распределений.
А.Р. Ржаницын рассмотрел также расчет надежности конструкций при воздействии нагрузок, представляющих собой случайные процессы [3].
Если совместное распределение случайных параметров 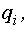 , характеризующих нагрузку, условия эксплуатации и внутренние свойства конструкции, отличается от нормального или логнормального, то надежность может быть определена по формуле типа (22.7), в интеграле которой
, характеризующих нагрузку, условия эксплуатации и внутренние свойства конструкции, отличается от нормального или логнормального, то надежность может быть определена по формуле типа (22.7), в интеграле которой 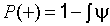 ,
, 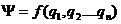 – совместная плотность распределения случайных параметров и интегрирование проводится по всем
– совместная плотность распределения случайных параметров и интегрирование проводится по всем 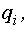 .
.
Строго говоря, формулы (22.8), (22.7) пригодны для случая однократного дискретного нагружения. К таким случаям можно отнести натяжение напрягаемой арматуры железобетонных мостовых конструкций, создание преднапряженных металлических конструкций, воздействие тяжелых монтажных нагрузок на пролетные строения мостов и др.
Для оценки надежности системы основание–сооружение по различным предельным состояниям рассмотрим решение, предложенное Н.Н. Ермолаевым [4]. При этом для дальнейших выкладок неравенство (22.1), заменив в нем буквенные обозначения, представим в виде:
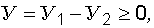 (22.9)
(22.9)
где 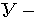 совокупный фактор, являющийся функцией случайных аргументов, определяющих числовые характеристики как "внутреннего" фактора
совокупный фактор, являющийся функцией случайных аргументов, определяющих числовые характеристики как "внутреннего" фактора 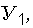 так и "внешнего" фактора
так и "внешнего" фактора 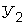 ;
; 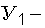 "внутренний" фактор системы сооружение–основание, характеризующий ее несущую способность или предельно допустимую деформацию;
"внутренний" фактор системы сооружение–основание, характеризующий ее несущую способность или предельно допустимую деформацию; 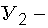 "внешний" фактор условий работы системы, характеризующий фактически действующие нагрузки при их наиболее невыгодном сочетании и обусловливающий наиболее тяжелые условия работы системы в отношении возможности потери несущей способности грунтовым основанием или появления наибольших деформаций.
"внешний" фактор условий работы системы, характеризующий фактически действующие нагрузки при их наиболее невыгодном сочетании и обусловливающий наиболее тяжелые условия работы системы в отношении возможности потери несущей способности грунтовым основанием или появления наибольших деформаций.
Учитывая выражение (22.9) и содержание понятия уровня надежности, соотношение для получения количественного показателя надежности системы основание–сооружение можно представить в виде:
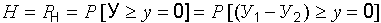 , (22.10)
, (22.10)
где 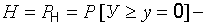 вероятность события, заключающегося в ненаступлении предельных состояний для системы основание–сооружение, численно равная уровню надежности системы.
вероятность события, заключающегося в ненаступлении предельных состояний для системы основание–сооружение, численно равная уровню надежности системы.
Так как наибольший практический интерес представляет предельное значение надежности, получаемое при наименьших затратах, то соотношение (22.10) для указанных условий может быть записано в виде:
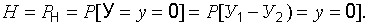 (22.11)
(22.11)
Для определения уровня надежности в общем случае необходимо знание плотности 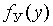 или функции
или функции 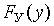 распределения совокупной величины
распределения совокупной величины 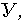 являющейся функцией многих случайных аргументов, от которых зависят факторы
являющейся функцией многих случайных аргументов, от которых зависят факторы 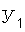 и
и 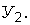
Применительно к случайной величине 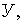 имеем
имеем
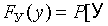
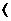
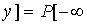
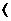
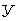
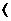
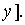 (22.12)
(22.12)
Учитывая, что
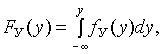 (22.13)
(22.13)
а также равенство (22.11), для уровня надежности 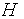 получаем:
получаем:
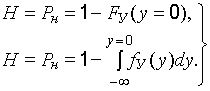 (22.14)
(22.14)
Как правило, закон распределения фактора 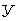 будет в достаточной мере сложным, если учесть множество случайных факторов, стоящих в правой части соотношения (22.9), от которых он зависит. Поэтому Н.Н. Ермолаев использовал приближенное соотношение в виде ряда Шарлье. В общем случае при
будет в достаточной мере сложным, если учесть множество случайных факторов, стоящих в правой части соотношения (22.9), от которых он зависит. Поэтому Н.Н. Ермолаев использовал приближенное соотношение в виде ряда Шарлье. В общем случае при 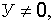 учитывая три первых члена ряда, получим
учитывая три первых члена ряда, получим
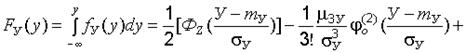
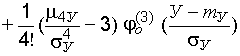 , (22.15)
, (22.15)
где 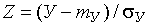 – нормированная случайная величина
– нормированная случайная величина 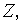 соответствующая случайной величине
соответствующая случайной величине 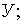
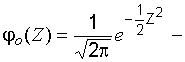 плотность нормального распределения случайной величины
плотность нормального распределения случайной величины 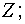
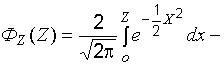 интеграл вероятностей (удвоенная функция Лапласа), определяемый для каждого из значений
интеграл вероятностей (удвоенная функция Лапласа), определяемый для каждого из значений 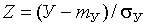 ;
; 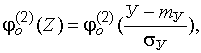
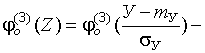 вторая и третья производные, определяемые по специальным таблицам для каждого заданного значения
вторая и третья производные, определяемые по специальным таблицам для каждого заданного значения 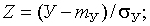
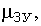
 третий и четвертый центральные моменты случайной величины совокупного фактора
третий и четвертый центральные моменты случайной величины совокупного фактора  ;
; 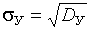 – среднеквадратическое отклонение фактора
– среднеквадратическое отклонение фактора  .
.
Так как для определения уровня надежности 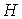 , согласно (22.14),
, согласно (22.14), 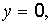 то по формуле (22.15)
то по формуле (22.15)
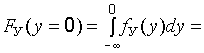
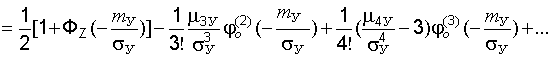 (22.16)
(22.16)
Подставив в соотношение (22.14) выражение для 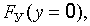 получаем:
получаем:
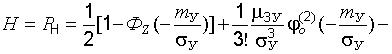
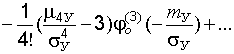 . (22.17)
. (22.17)
Учитывая, что 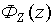 и
и 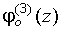 являются нечетными функциями, а
являются нечетными функциями, а 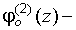 четной, получим:
четной, получим:
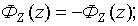
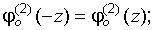
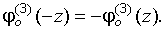
Тогда для уровня надежности 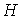 получаем следующее выражение:
получаем следующее выражение:
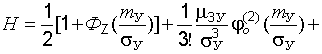
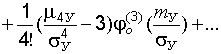 . (22.18)
. (22.18)
Вводя коэффициент вариации случайной величины 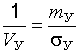 и обозначая
и обозначая 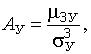
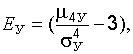 получим выражение для определения расчетного уровня надежности:
получим выражение для определения расчетного уровня надежности:
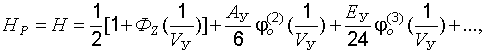 (22.19)
(22.19)
где 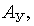
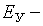 асимметрия и эксцесс фактора
асимметрия и эксцесс фактора 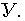
Имея в виду выражение (22.9), для определения числовых характеристик функции  , являющейся разностью двух независимых случайных величин, получаем следующие формулы:
, являющейся разностью двух независимых случайных величин, получаем следующие формулы:
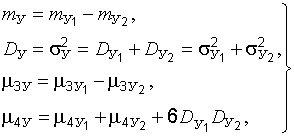 (22.20)
(22.20)
где 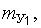
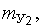
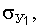
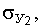
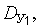
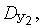
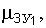
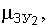

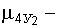 соответственно математические ожидания, среднеквадратические отклонения, дисперсии и центральные моменты третьего и четвертого порядка факторов
соответственно математические ожидания, среднеквадратические отклонения, дисперсии и центральные моменты третьего и четвертого порядка факторов 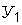 и
и 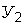 как случайных величин. Указанные числовые характеристики определяются как характеристики функций случайных аргументов, от которых они зависят.
как случайных величин. Указанные числовые характеристики определяются как характеристики функций случайных аргументов, от которых они зависят.
Для практических приложений в проектировании транспортных сооружений чрезвычайно важным является вопрос обеспечения требуемой надежности при возможности варьирования несущей способностью 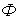 (“внутренним” фактором
(“внутренним” фактором 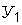 ) в соотношениях (22.1) и (22.9), которые отображают совокупность прочностных или деформативных показателей материала конструкций и грунтов основания, с учетом вида их напряженного состояния и геометрических размеров конструкции и фундамента.
) в соотношениях (22.1) и (22.9), которые отображают совокупность прочностных или деформативных показателей материала конструкций и грунтов основания, с учетом вида их напряженного состояния и геометрических размеров конструкции и фундамента.
Согласно существу вероятностного толкования понятия надежности, коэффициент запаса 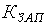 (коэффициент надежности
(коэффициент надежности 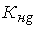 ) в работе конструкции при расчете на прочность или устойчивость, а также при условии, что
) в работе конструкции при расчете на прочность или устойчивость, а также при условии, что 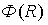 и
и 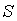 распределены по нормальному закону, определяется по формуле
распределены по нормальному закону, определяется по формуле 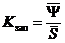 .
.
Учитывая, что 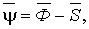 можно получить условие
можно получить условие
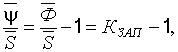 (22.21)
(22.21)
откуда
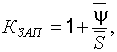 (22.22)
(22.22)
где 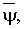
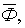
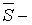 математические ожидания соответствующих факторов.
математические ожидания соответствующих факторов.
Имея соотношения (22.21), (22.22) и учитывая, что 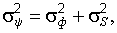 можно определить характеристику безопасности
можно определить характеристику безопасности 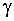 по формуле (22.6) через коэффициент запаса
по формуле (22.6) через коэффициент запаса 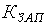 в виде:
в виде: 
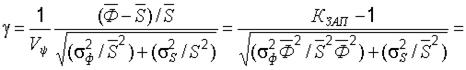
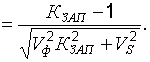 (22.23)
(22.23)
Решая выражение (22.23) относительно коэффициента запаса 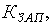 получим
получим
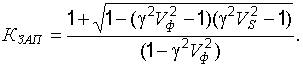 (22.24)
(22.24)
При логнормальном распределении 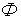 и
и 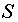 коэффициент запаса
коэффициент запаса 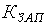 получит выражение:
получит выражение:
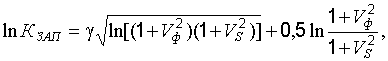 (22.25)
(22.25)
где 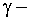 характеристика безопасности, определяемая по формуле (22.8).
характеристика безопасности, определяемая по формуле (22.8).
Уровень надежности 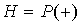 при нормальном и логнормальном распределениях факторов
при нормальном и логнормальном распределениях факторов 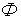 и
и 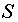 устанавливается по формуле (22.7).
устанавливается по формуле (22.7).
При экспоненциальном законе распределения 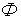 и
и 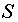 выражение коэффициента запаса
выражение коэффициента запаса 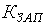 с использованием условия
с использованием условия 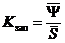 , получит следующий вид:
, получит следующий вид:
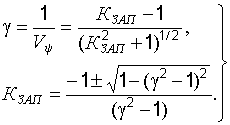 (22.26)
(22.26)
Для оценки уровня надежности 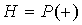 в этом случае получено следующее выражение:
в этом случае получено следующее выражение:
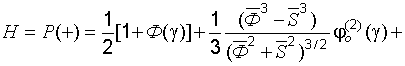
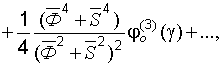 (22.27)
(22.27)
где 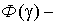 интеграл вероятности (функция Лапласа);
интеграл вероятности (функция Лапласа);
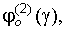
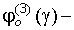 вторая и третья производные, определяемые по специальным таблицам [4];
вторая и третья производные, определяемые по специальным таблицам [4];
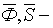 математическое ожидание соответствующих экспоненциальных распределений;
математическое ожидание соответствующих экспоненциальных распределений;
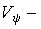 коэффициент вариации совокупного случайного фактора,
коэффициент вариации совокупного случайного фактора,
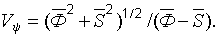
При расчете грунтовых оснований на прочность по способу Н.Н. Ермолаева нормированная случайная величина 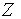 определяется по аналогии с выражением (22.23) и имеет следующий вид:
определяется по аналогии с выражением (22.23) и имеет следующий вид:
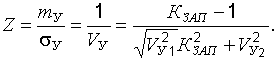 (22.28)
(22.28)
Решая соотношение (22.28) относительно 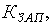 получим:
получим:
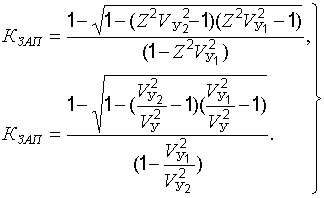 (22.29)
(22.29)
Подставив в правую часть соотношения (22.19) для определения уровня надежности вместо 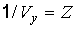 его выражение (22.28), имеем:
его выражение (22.28), имеем:
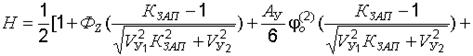
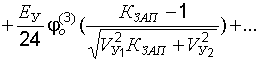 . (22.30)
. (22.30)
Как показывают численные расчеты по формулам (22.16), (22.18), (22.19) влияние членов расчетных соотношений для определения надежности, зависящих от третьего и четвертого центрального моментов, обычно не превосходит нескольких процентов. Это влияние тем меньше, чем больше коэффициент запаса и чем меньше коэффициент вариации физико-механических свойств грунтовых оснований. Поэтому для грубых прикидочных расчетов можно использовать указанные формулы без учета третьего и четвертого членов. В этом случае 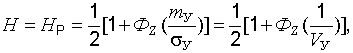 (22.31)
(22.31)
где 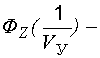 удвоенный интеграл Лапласа.
удвоенный интеграл Лапласа.
Использование формулы (22.31) равносильно принятию для совокупного фактора 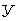 нормального закона распределения.
нормального закона распределения.
Использование соотношений (22.7), (22.23); (3.10), (22.25); (22.26), (22.27), (22.30) при различных законах распределения факторов 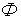 и
и 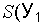 и
и 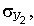 позволяет решать следующие практически важные задачи:
позволяет решать следующие практически важные задачи:
1) определять уровень надежности 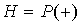 при заданных коэффициентах запаса
при заданных коэффициентах запаса 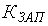 , числовых характеристиках случайных величин
, числовых характеристиках случайных величин 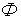 и
и 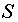
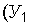 и
и 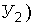 и их коэффициентах вариации;
и их коэффициентах вариации;
2) определять требуемый коэффициент запаса для обеспечения заданного уровня надежности конструкции или грунтового основания при известных числовых характеристиках случайных величин 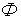 и
и 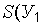 и
и 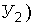 и их коэффициентах вариации.
и их коэффициентах вариации.
Каждая из указанных задач имеет свою область преимущественного использования. Решение первой задачи представляет большой интерес при оценке уровня надежности существующих эксплуатируемых конструкций и грунтовых оснований сооружений. Решение второй задачи имеет преимущественное значение в стадии проектирования конструкций и грунтовых оснований сооружений.
 2017-12-14
2017-12-14 1299
1299
