Наклонное падение лучей

Если плоская волна падает на решетку наклонно под углом q, то разность хода между соседними пучками становятся равной АС-ДВ=d sinq-sin (рис. 7).

Рис. 7

Характер дифракционной картины в основном сохраняется. Положение главных максимумов определяется условием

d(sin (1.18)

- направление на главный максимум порядка m
(m=0, ).

Преобразуем соотношения 1.18, воспользовавшись тригонометрической формулой разности синусов двух углов, т.е.

sin . (1.19)

С учетом 1.19 формула 1.18 преобразуется к виду

(1.20)

Если решетка довольна груба, т.е. период ее d значительно больше , то углы дифракции малы и угол мало отличается от . В таком случае можно положить:

и 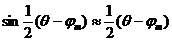(1.21)

С учетом (1.21) формула (1.20) принимает вид:

(1.22)

Сравним формулу 1.22 с формулой для нормального падения волнового фронта на решетку dsin или d , если угол мал. Это сравнения показывает, что угол между направлениями на нулевой максимум и на ненулевые максимумы () вычисляется так же, как если бы падение было нормальным, но решетка имела бы уменьшенный период, а именно . Следовательно, роль периода решетки d играет величина dcos , которая может быть сделана очень малой. Скользящее падение лучей как бы уменьшает период решетки и увеличивает углы дифракции. Таким путем удается получать отчетливые дифракционные спектры даже от очень грубых решеток, например от граммофонных пластинок. Последние позволяют в демонстрационной аудитории получать в белом свете довольно красивые дифракционные спектры разных порядков.