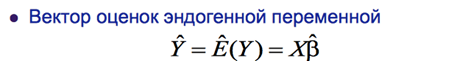
Классическая множественная регрессионная модель: числовые характеристики вектора оценок эндогенной переменной

 

 

 

 

 

 

Классическая множественная регрессионная модель: числовые характеристики вектора ошибок прогнозов

 

Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x₁,...,x_р), где у - зависимая переменная (результативный признак); х₁,...,х_р - независимые переменные (факторы).

ε=(ε1,...,εn)T- вектор-столбец случ.возмущений. Относительно него принимаются следующие предпосылки - условия Гаусса:

1. E(ε)=0;

2. Cεε=E(εεT)=σ2In - автоковар. матрица вектора возмущений, In - единич. матрица n*n;

3. ε~N(0,σ2In) - норм. распределенный случ.вектор с нулевым мат.ожиданием и автоковар.матрицейCεε.

Как и в случае парной модели, оценка дисперсии возмущений выражается так:

σ2 = ∑e2t=eTe, где

e = Y-Ŷ = Y - Xb~ =Y - XAY = Y-NY = (I-N)Y = MY = М(Xb+ε) = Мε - n-мерный вектор-столбец остатков регрессии - случайный вектор. Матрицы M и N - идемпотентны.

Несмещенной оценкой дисперсии возмущений является оценка вида s2= σ~2=∑e2t/(n-k)=eTe/(n-k), где k - число параметров модели.

Коэффициент детерминации в парной регрессионной модели: определение, расчетная формула, смысл компонентов формулы, смысл коэффициента детерминации. Скорректированный коэффициент детерминации во множественной регрессионной модели

Линейная парная регрессионная модель используется для описания взаимосвязи двух переменных Y и X, если имеется предположения, что между ними существует линейная стохастическая зависимость: y=a+bx+ε, где а и b – параметры модели (постоянные неизвестные коэффициенты); Х- независимая переменная; Y— зависимая переменная; ε - случайная переменная (возмущение, ошибка), возникающая из-за влияния различных неучтенных факторов.

Уравнение для отдельных наблюдений зависимой переменной Y записывается в виде: yt=a+bxt+εt

где ХtYt, - набор данных (наблюдений), t = 1, 2,..., n;

Xt – экзогенная переменная модели); εt - случайная ошибка в наблюдении t.

Если отклонение зависимой переменной Yt, от ее выборочного среднего значения представить в виде суммы двух отклонений:

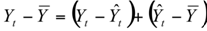
и выборочную дисперсию var(Y) можно представить в виде двух частей:

Часто это уравнение записывают так:

TSS = ESS + RSS,

где TSS = var(Y) – полная дисперсия (общая сумма квадратов отклонений зависимой переменной от ее выборочного значения);

ESS = Σ(Yt-Ŷt)2 – часть дисперсии, необъясненная регрессией (т.к. она содержит ошибки регрессии εt);

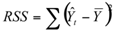- часть дисперсии, объясненная регрессией (объясненная сумма квадратов отклонений).

Качество подгонки регрессионной модели к наблюденным значениям Yt оценивается при помощи статистики R2 (коэффициента детерминации).

Коэффициент детерминации определяется по формуле:

R2 = 1-ESS / TSS = RSS / TSS; 0≤R2≤1

Чем ближе значение коэффициента детерминации к 1, тем лучше качество подгонки и прогноз Ŷ более точно аппроксимирует Y.

Для проверки значимости коэффициента детерминации используется F-статистика:

где k - число независимых переменных.

Связь между статистиками F и R2 для случая парной регрессии (k = 1) имеет вид