Запишем уравнение Эйнштейна для этого случая. Т. к. энергии такого кванта хватает только на то, чтобы выбить электрон, и на его разгон энергии уже нет (см. рис. 12), составляющая 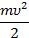 будет равна нулю:
будет равна нулю:
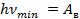
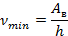 ,
,
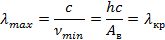 – красная граница фотоэффекта.
– красная граница фотоэффекта.
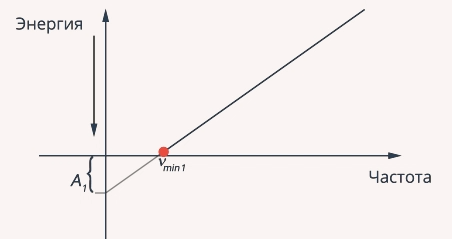
Рис. 12. Зависимость кинетической энергии фотоэлектрона от частоты падающего света
Частота или длина волны, соответствующие красной границе фотоэффекта, зависят от вещества и определяются величиной работы выхода электрона из данного вещества (см. рис. 13).
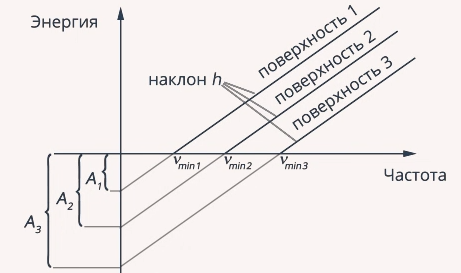
Рис. 13. Зависимость частоты (длины волны) от вещества
Суммарная энергия квантов 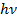 в световом потоке, падающем на металл, – это интенсивность света. Если мы изменяем интенсивность света данной частоты, то это значит, что мы изменяем количество фотонов, а значит, и количество фотоэлектронов. Скорость каждого выбитого из металла электрона от интенсивности света не зависит.
в световом потоке, падающем на металл, – это интенсивность света. Если мы изменяем интенсивность света данной частоты, то это значит, что мы изменяем количество фотонов, а значит, и количество фотоэлектронов. Скорость каждого выбитого из металла электрона от интенсивности света не зависит.
Задача
Красная граница фотоэффекта для калия 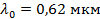 . Какую максимальную скорость могут иметь фотоэлектроны, вылетающие с поверхности калиевого фотокатода при облучении его светом с диной волны
. Какую максимальную скорость могут иметь фотоэлектроны, вылетающие с поверхности калиевого фотокатода при облучении его светом с диной волны 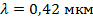 ?
?
Анализ условия.
- В задаче описан фотоэффект, значит, будем использовать уравнение Эйнштейна для фотоэффекта: 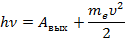 .
.
- Красная граница фотоэффекта – это минимальная частота, при которой наблюдается фотоэффект, при этом энергии фотона хватает только на выбивание электрона из вещества, но кинетическая энергия электрону не сообщается: 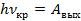 .
.
- Мы легко переходим от частоты к длине волны, используя формулу 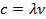 .
.
Решение
Применим к данной задаче уравнение Эйнштейна для фотоэффекта и выражение для красной границы. В задаче заданы значения длин волн, поэтому сразу перейдем от частот к длинам волн по формуле 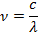 . Запишем:
. Запишем:
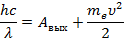
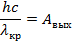
Получили систему уравнений, решив которую, найдем максимальную скорость электрона. Получим ответ около 580 км/с.
Математическая часть решения задачи
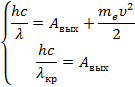
Подставим выражение для работы выхода из второго уравнения в первое:
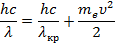
Выразим отсюда искомую скорость:
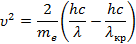
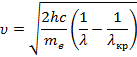
Вычислим:
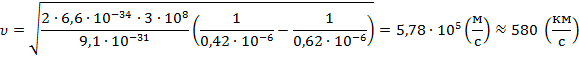
 2017-12-14
2017-12-14 4564
4564








