Решение:
1. Посчитаю количество символов в данном сообщении Q = 53
2. Найду частоты появления (вероятности) символов и занесу их в таблицу 1.
Таблица 1.
Таблица частот появления символов
| С | а | м | р | с | к | и | й | г | |
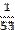
| 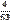
| 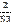
| 
| 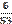
| 
| 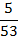
| 
| 
| 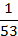
|
| о | у | д | т | в | е | н | ы | э | ч |
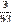
| 
| 
| 
| 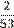
| 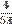
| 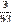
| 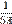
| 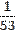
| 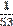
|
3. Кодируемые знаки расположу в порядке убывания их вероятностей (рi)
4. На каждом шаге две последние позиции списка (жирным шрифтом) суммирую и заменяю одной (выделенной цветом), которой приписываю данный результат сложения. Далее вновь сортирую список вероятностей, при этом сохраняю информацию о том, какие именно символы объединялись на каждом этапе. Процесс продолжаю до тех пор, пока не останется единственная позиция, вероятность которой равна 1.
Таблица 2.
Алгоритм Хаффмана
| Знаки | Pi | Вспомогательные столбцы | |||||||
| с | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| и | 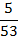
| 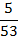
| 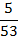
| 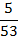
| 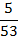
| 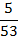
| 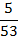
| 
| 
|
| а | 
| 
| 
| 
| 
| 
| 
| 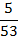
| 
|
| р | 
| 
| 
| 
| 
| 
| 
| 
| 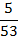
|
| е | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| к | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| й | 
| 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
| 
| |
| о | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| т | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| н | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| м | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| у | 
| 
| 
| 
| 
| 
| 
| 
| |
| в | 
| 
| 
| 
| 
| 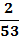
| 
| ||
| С | 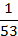
| 
| 
| 
| 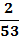
| 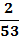
| |||
| г | 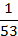
| 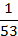
| 
| 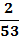
| 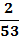
| ||||
| д | 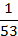
| 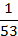
| 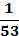
| 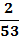
| |||||
| ы | 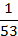
| 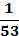
| 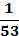
| ||||||
| э | 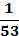
| 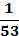
| |||||||
| ч | 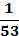
|
| Вспомогательные столбцы | ||||||||||
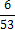
| 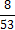
| 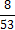
| 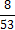
| 
| 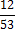
| 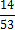
| 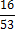
| 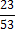
| 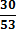
| |
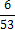
| 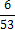
| 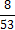
| 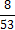
| 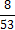
| 
| 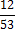
| 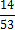
| 
| 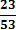
| |
| 
| 
| 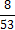
| 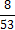
| 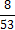
| 
| 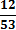
| 
| ||
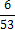
| 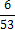
| 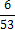
| 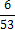
| 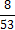
| 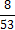
| 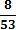
| 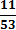
| |||
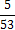
| 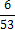
| 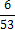
| 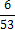
| 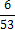
| 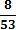
| 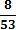
| ||||
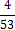
| 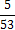
| 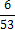
| 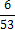
| 
| 
| |||||
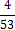
| 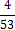
| 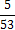
| 
| 
| ||||||
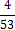
| 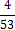
| 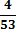
| 
| |||||||
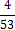
| 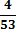
| 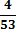
| ||||||||
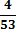
| 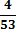
| |||||||||
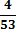
|
5. Строю кодовое дерево. Корню дерева ставлю узел, вероятность которого равна 1. Затем каждому узлу приписываю два потомка с вероятностями, которые участвовали в образовании значения вероятности этого узла.
6. Данный процесс продолжаю до достижения узлов, соответствующих вероятностям исходных знаков.
Одной из ветвей, выходящей из каждого узла, например, с меньшей вероятностью, ставлю в соответствие символ 0, а с большей — 1. Спускаюсь от корня к нужному символу и, тем самым, получаю код этого символа.
Таким образом, получаю кодовое дерево (см. Приложение 1).
Составлю таблицу соответствия символов с полученным кодом Хаффмана:
Таблица 3.
Таблица соответствия символов с полученным кодом Хаффмана
| Символ | Вероятность | Код Хаффмана | Символ | Вероятность | Код Хаффмана |
| С | 
| н | 
| ||
| и | 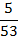
| м | 
| ||
| а | 
| у | 
| ||
| р | 
| в | 
| ||
| е | 
| С | 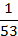
| ||
| к | 
| г | 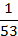
| ||
| й | 
| д | 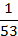
| ||

| ы | 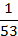
| |||
| о | 
| э | 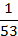
| ||
| т | 
| ч | 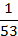
|
Чтобы убедиться в том, что исходное сообщение сжалось, сравню объемы данного сообщения, закодированного с помощью ASCII-кодов и закодированного с помощью алгоритма Хаффмана.
Рассчитаю объем сообщения после кодирования кодом Хаффмана: суммирую произведение частоты встречаемости символа и количества 0 и 1 соответствующее этому символу по коду Хаффмана.
I1=6*3+5*3+4*4+4*4+4*4+3*4+3*4+3*4+3*4+3*4+3*4+2*5+2*5+2*5+1*6+1*6+1*6+1*6+1*6+1*6 = 18+15+48+72+30+36 = 219 бит
Сообщение в памяти компьютера закодировано с помощью ASCII-кодов, каждый символ весит 8 бит. Значит, объем исходного сообщения найду по формуле:
I = K*i,
где: K — количество символов в сообщении,
i — вес одного символа в битах,
I — информационный объем данного сообщения.
В моей задаче K = 53, i = 8 бит, значит, I2 = 8*53 = 424 бит
Коэффициент сжатия:
k = I2/I1
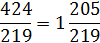
k= 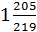
Ответ: закодированное данное сообщение методом Хаффмана выглядит так: 110001101111101101110101000011000001001011100000100100111001100111011101010001111111111010110011011001000100101101111110110100100001101001001110100011110011011000011000001001011110001100001111111011010100000011111010111
Декодирование
Рассмотрю на следующем примере, как происходит процесс декодирования.
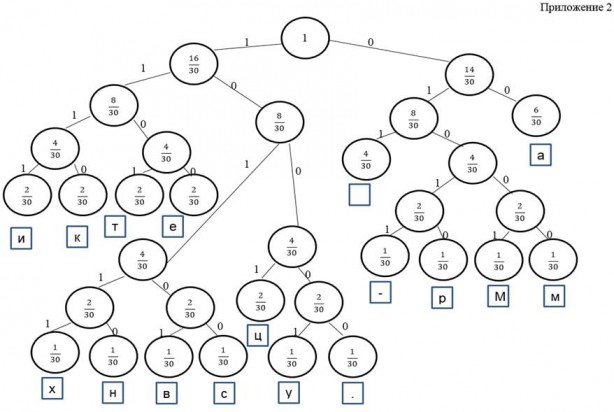
Задача № 2. Дано дерево Хаффмана (см. Приложение 2) и битовая последовательность (закодированное сообщение):
Получить исходное сообщение (раскодировать).
Решение:
Для получения текста по этой последовательности многократно повторяю траверс от корня к листьям, перемещаясь в левое поддерево, если встречен 1, и в правое поддерево, если 0. Каждый раз по достижению листа символ в нём добавляю в полученный текст и снова начинаю процедуру от корня, продолжая просмотр последовательности с того же места.
Ответ: Математика — царица всех наук.
Заключение
В работе я рассмотрела основные понятия теории графов, виды графов. Описала алгоритм Хаффмана, метод сжатия информации, кодирования и декодирования.
Применяя теорию графов и используя алгоритм Хаффмана, закодировала и декодировала информацию, построив кодовое дерево.
С помощью графов решать задачи очень удобно, интересно, увлекательно. Теория графов обеспечивает эффективное сжатие информации.

Список литературы:
1.Березина Л.Ю. Графы и их применение. М.: Просвещение, 1979. — 143 с. с ил.
2.Додонова Л.Н. Конспект лекций по дисциплине «Теория конечных графов и ее применения». Самара, 2010. — С. 52.
3.Камерон П., ван Линт Дж. Теория графов, теория кодирования и блок-схемы М.: Наука, 1980, — 140 стр.
4.Фурсов В.А. Лекции по теории информации: Учебное пособие под редакцией Н.А. Кузнецова. Самара: Издательство Самар. гос. аэрокосм. ун-та, 2006. — 148 с.: ил.
Пожалуйста, не забудьте правильно оформить цитату:
Васильева М.В. ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ В КОДИРОВАНИИ И ДЕКОДИРОВАНИИ ИНФОРМАЦИИ // Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ: сб. ст. по мат. XXIX междунар. студ. науч.-практ. конф. № 2(28). URL: http://sibac.info/archive/technic/2(28).pdf (дата обращения: 03.09.2017)
 2017-12-14
2017-12-14 383
383







