Метод линейной развертки
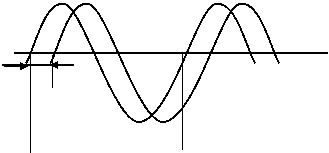
Исследуемые сигналы U1 и U2 подают на входы каналов вертикального отклонения двухканального осциллографа Y1 и Y2 и получают осциллограмму этих сигналов (см. рисунок).
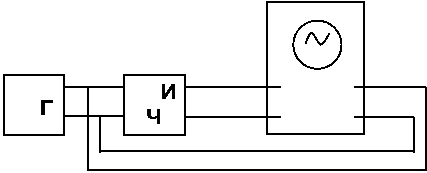
U2 Y1 Y2 U1
 |
l
 L
L
По линейным размерам осциллограммы l и L определяют фазовый сдвиг:
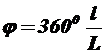
погрешность измерения составляет 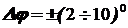
Метод синусоидальной развертки (фигур Лиссажу).
Если в ЭО установить режим внешней развертки и подать на входы X и Y сигнолы, между которыми необходимо измерить фазовый сдвиг, то на экране осциллографа можно получить фигуру Лиссажу (см. рисунок):
 |
b
Б y
a
x
A
Измерение линейных размеров фигуры позволяет вычислить фазовый сдвиг:
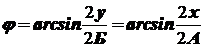
Когда a>b, j > 90o, в этом случае 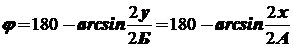
Погрешность оценивают по методике оценки погрешности косвенных измерений, и она составляет 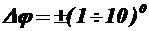 в зависимости от размера фазового сдвига и погрешности измерения линейных размеров.
в зависимости от размера фазового сдвига и погрешности измерения линейных размеров.
При выполнении условия А=Б 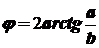 , а
, а 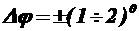
Равенство А=Б устанавливают при помощи ступенчатого и плавного регуляторов коэффициентов отклонения каналов X и Y.
Измерение фазового сдвига с преобразованием его во временной интервал и напряжение.
Метод реализуют с помощью следующей структурной схемы:
 |
 U1
U1
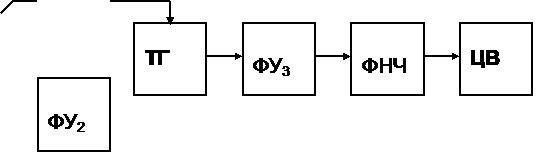 |

 U2
U2
 |  | ||
ФУ1,2 – формирующие устройства, которые формируют из гармонического сигнала сигнал с крутыми фронтами.
ФУ3 – формирующее устройство для формирования сигнала с калиброванным пиковым значением UР.
ФНЧ – фильтр нижних частот для выделения постоянной составляющей сигнала UСР.
ЦВ – цифровой вольтметр постоянного напряжения.
БФ – блок формирования временного интервала Dtj.
На рисунке показаны временные диаграммы сигналов в разных точках структурной схемы:
 U1,U2
U1,U2
 T
T
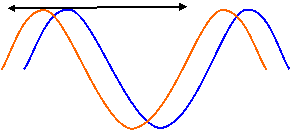







 t
t

 UФ1
UФ1
 |  |
 t
t
 |
UФ2
 |  | ||
 t
t
UФ3 


 UР Dtj
UР Dtj

t j = 360Dtj/T

UФНЧ 
UСР
 |
 t
t
Среднее значение напряжения на выходе ФНЧ определяется выражением: 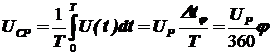
Следовательно, показание ЦВ будет пропорционально фазовому сдвигу j
Источники погрешности измерения:
1)погрешность формирования временного интервала Dtj
2)нестабильность напряжения Up
3)погрешность ЦВ
Цифровой фазометр с времяимпульсным
преобразованием за 1 период.
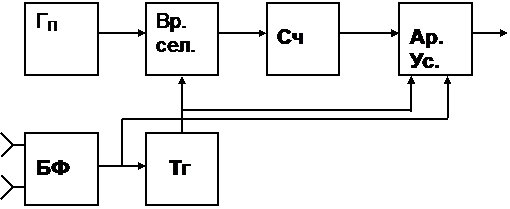
Структурная схема такого фазометра имеет вид:
 UСЕЛ К ЦУО
UСЕЛ К ЦУО
fГ
UТГ
U1
U2 UБФ
ГП - генератор коротких импульсов с частотой следования fГ;
Вр. Сел. – временной селектор (электронный ключ, электронный коммутатор);
Сч – счетчик импульсов;
Тг – триггер;
Ар.Ус. – арифметическое устройство;
БФ – блок формирования интервала Dtj (см. предыдущую схему).

 UБФ
UБФ




 Dtj
Dtj
 |  |
| ||||
 UТГ
UТГ
Т
 | |||
 |
 UСЕЛ NT
UСЕЛ NT
 | |||
 |
N
NDt
Выразим фазовый сдвиг через показания счетчика:
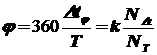 , здесь k – коэффициент пропорциональности.
, здесь k – коэффициент пропорциональности.
Источники погрешности:
погрешность, вносимая БФ;
погрешность дискретизации (квантования)
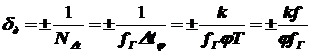
Из формул видно, что с ростом частоты исследуемого сигнала f погрешность дискретизации увеличивается и на высоких частотах становится недопустимо большой.
Цифровой фазометр средних значений
(с постоянным временем измерения)
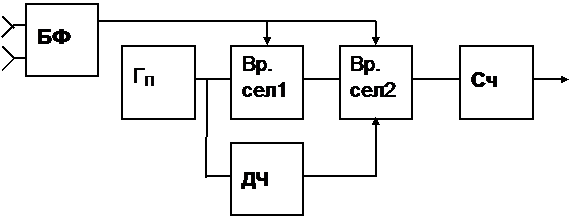 UБФ
UБФ
U1
U2 fГ
UСЧ К ЦОУ
UДЧ
ДЧ – делитель частоты в n раз – формирует временной интервал TИЗМ, в течение которого происходит измерение;
ЦОУ – цифровое отсчетное (отображающее) устройство;
остальные обозначения соответствуют предыдущей схеме.
Работа схемы проиллюстрирована временными диаграммами:
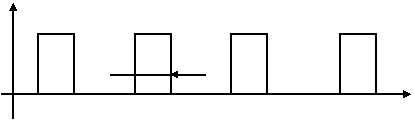 UБФ
UБФ
T
 |
Dtj
 t
t
 UДЧ
UДЧ
ТИЗМ

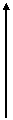 UСЧ
UСЧ
NСЧ
 | |||
 |
Количество пачек импульсов на выходе Вр.сел2 m: 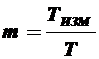
Количество импульсов в пачке Nпач: Nпач = DtjfГ
Тогда общее количество импульсов, накопленное в счетчике за время измерения TИЗМ:
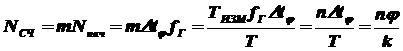 , где
, где 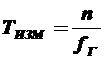
Если коэффициент деления частоты fГn=360, то 1 импульс счетчика будет соответствовать 1 градусу фазового сдвига и показания счетчика будут равны фазовому сдвигу. Для повышения точности измерения достаточно увеличить коэффициент деления частоты до 3600 или 36000 и погрешность индикации уменьшится до 0,1° или 0,01° соответственно.
Погрешность дискретизации определяется двумя факторами: случайным временным положением интервалов Dtj относительно счетных импульсов dд1 и случайным положением интервала TИЗМ относительно интервалов Dtj - dд2: 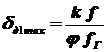 ;
; 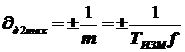 .
.
Суммарная погрешность дискретизации равна: 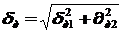

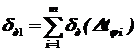
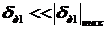 т.к.
т.к. 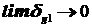
Источники погрешности:
- погрешность дискретизации;
- погрешность формирования интервала Dtj (БФ).
Измерение параметров двухполюсников.
О параметрах двухполюсников.
Двухполюсник, в общем случае, представляет элемент, сопротивление которого может быть записано в виде комплексного выражения в алгебраической форме записи 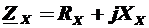 . Здесь Rx и Xx соответственно резистивное и реактивное сопротивления двухполюсника.
. Здесь Rx и Xx соответственно резистивное и реактивное сопротивления двухполюсника.
Сопротивление двухполюсника может быть записано в виде комплексного выражения в показательной форме записи 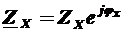 . Здесь Z x и jx соответственно модуль и угол сопротивления двухполюсника. Они могут быть определены соответствующими выражениями:
. Здесь Z x и jx соответственно модуль и угол сопротивления двухполюсника. Они могут быть определены соответствующими выражениями: 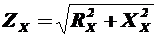 ;
; 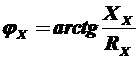 .
.
Добротность 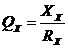 и тангенс угла потерь
и тангенс угла потерь 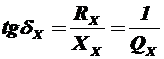 являются обратными величинами.
являются обратными величинами.
Угол потерь и угол сопротивления двухполюсника в сумме дают прямой угол 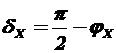 . На векторной диаграмме представлены эти углы.
. На векторной диаграмме представлены эти углы.



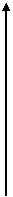 XX ZX
XX ZX
 dX
dX

jX
 RX
RX
Методы измерения параметров двухполюсников на переменном токе
1. Мостовой метод получил широкое распространение благодаря высокой точности измерения. На рисунке представлена схема четырехплечего моста типа Уитстона
A
 Z1 Z2
Z1 Z2
|
Z4 Z3
B
|
G
. В одну из диагоналей моста включают генератор Г, а в другую – индикатор И. Изменяя сопротивление плеч моста, можно добиться такого состояния схемы, когда индикатор покажет отсутствия тока в диагонали АВ моста. Мост в таком состоянии называют уравновешенным. Аналитически условие равновесия моста можно записать 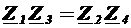 . В показательной форме
. В показательной форме 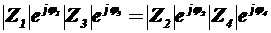 . Равенство двух комплексных чисел возможно, если
. Равенство двух комплексных чисел возможно, если
 или
или
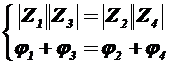 Эти выражения широко используют при анализе схем мостов.
Эти выражения широко используют при анализе схем мостов.
Примеры схем мостов:
1. Дана схема моста. Выразить неизвестные элементы.
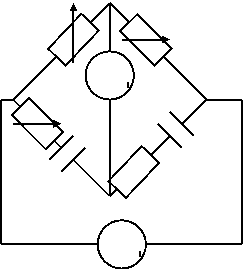 R1 R2
R1 R2
|
R0
CX
C0 RX
|
В соответствии с условием равновесия моста запишем 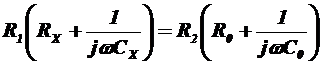 , откуда получим
, откуда получим
 ;
; 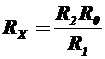 ;
; 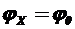
Угол потерь: 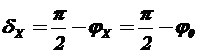
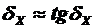 Это равенство справедливо до 10о с погрешностью не менее 1%.
Это равенство справедливо до 10о с погрешностью не менее 1%.
2. Надо разработать мост для измерения сопротивления индуктивного характера (желательно использовать образцовый конденсатор).
Схема может выглядеть так:




 R0
R0
 R2
R2
|










 C0
C0
|
 LX
LX 


 R4
R4
RX
|

 |
В соответствии с условием равновесия моста запишем 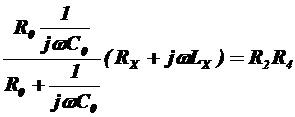 , откуда получим
, откуда получим
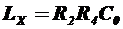
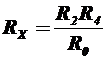
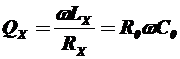
Недостатки мостового метода:
паразитные связи (емкостные, так как  , то с ростом частоты влияние паразитных связей возрастает).
, то с ростом частоты влияние паразитных связей возрастает).
Резонансный метод измерения параметров двухполюсников.
На частотах более 50кГц для измерения параметров двухполюсников применяют метод, в основе которого лежит явление резонанса. Схема такого метода представлена на рисунке.



 CX
CX
 |  |  | |||||
| |||||||














 L
L





 1 2 3 4 C0
1 2 3 4 C0





 E0 ZX 5
E0 ZX 5
 | |||
 |
G – генератор гармонических колебаний, перестраиваемый по частоте в широких пределах; L C0 – измерительный контур;
безымянные четыре емкости – емкостные делители напряжения, ослабляющие степень влияния генератора и вольтметров на измерительный контур.
В контуре можно достигнуть резонанса путем изменения емкости С0 или частоты генератора.
После настройки на резонанс отношение напряжений на емкости или индуктивности к вводимому напряжению в контур примерно равно добротности.
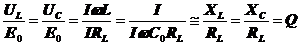
Прибор прямо измеряет добротность, если напряжение Е0 поддерживается постоянным. Такой прибор называют измерителем добротности или куметром.
Резонансную частоту через элементы контура определяют:
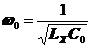
 LX RX - эквивалентная схема
LX RX - эквивалентная схема

 CX
CX
 |  |

 X реальная
X реальная
 |
Идеальная
|

 f
f
Измеренное по идеальной характеристике – действительное значение катушки индуктивности.
Измеренное по реальной характеристике – действующее значение катушки индуктивности.
Чтобы измерить С L надо провести измерения на двух частотах
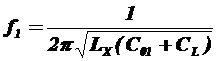
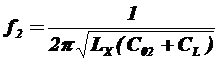
отсюда можно выразить С L= 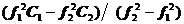 =
= 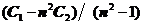
Измерения параметров двухполюсников измерителем добротности проводят в два этапа:
1. Измеряют параметры образцового резонанса контура, состоящего из встроенного в прибор образцового конденсатора и образцовой сменной катушки. Образцовую сменную катушку выбирают таким образом, чтобы частота, на которой будут выполнять измерения, попадала в диапазон частот, указанный на образцовой катушке. Настроив на заданной частоте образцовый контур в резонанс путем изменения образцовой емкости, снимают показания добротности и образцовой емкости, которые обозначим через Q1 и С1 .
2. В зависимости от величины модуля сопротивления, измеряемый объект включают параллельно или последовательно в образцовый контур. После этого, производят настройку образованного контура в резонанс на заданной частоте изменением образцовой емкости. Добротность контура и образцовую емкости обозначим через Q2 и C2 .
С помощью формул производят вычисления параметров измеряемого объекта.
Запишем выражения для первого этапа.
Зажимы 3-4 замкнуты, тогда сопротивление между точками 1-5 выразим 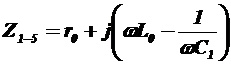 , в момент резонанса
, в момент резонанса 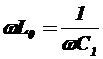 ,
, 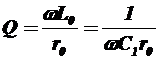
Запишем выражения для второго этапа.
В зажимы 3-4 включим ZX, тогда сопротивление между точками 1-5 выразим 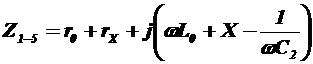
Из этих выражений можно вывести значение реактивной и резистивной составляющих сопротивлений. В момент резонанса выражение в скобках равно нулю, поэтому
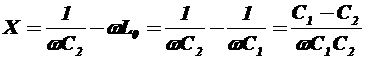 ,
, 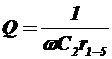
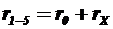
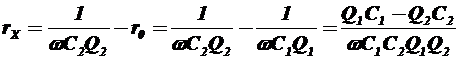
Аналогично можно вывести формулы для параллельного подключения к контуру измеряемого объекта.
Резонансный метод измерения параметров двухполюсников можно характеризовать:
достоинства - простота, дешевизна;
недостатки - т.к. измерения проводятся на ВЧ, то велика погрешность измерения вольтметрами, неточность настройки в резонанс.
 2017-12-14
2017-12-14 832
832












