Задания для самоконтроля
1.Вычислите неопределенные интегралы:
а) 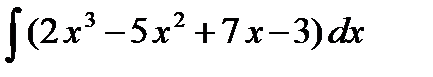 =
= 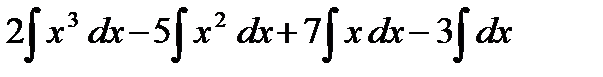 =
= 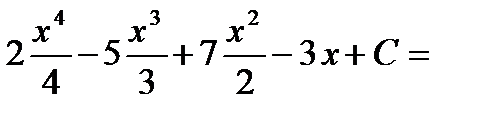
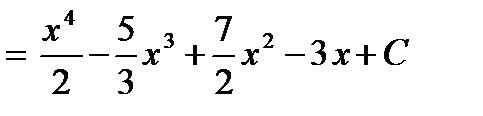
б) 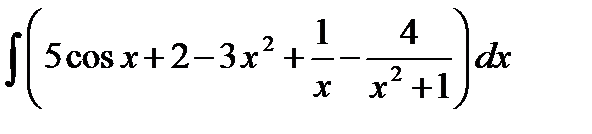 =
= 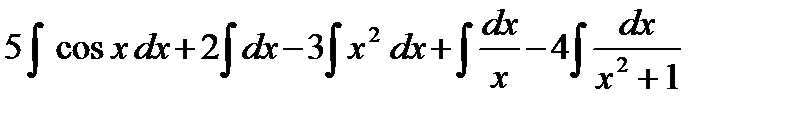
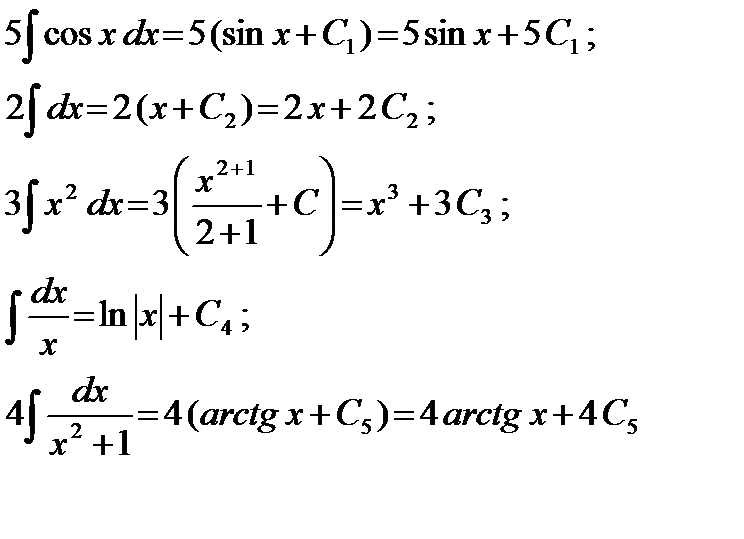
Таким образом,
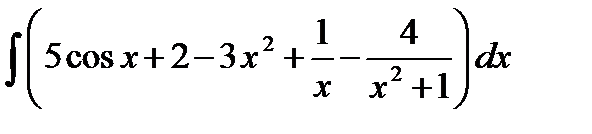 =
= 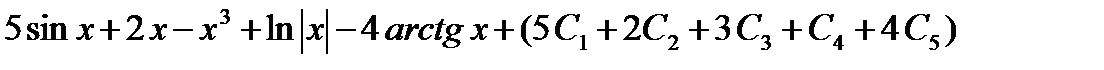
Обычно все произвольные постоянные суммируют, результат обозначают одной буквой
С = 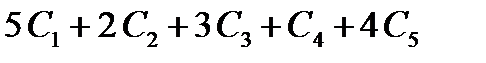 , поэтому окончательно получаем
, поэтому окончательно получаем
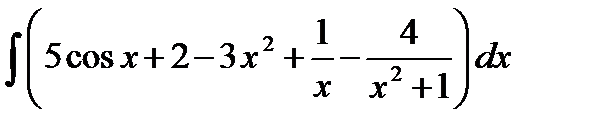 =
= 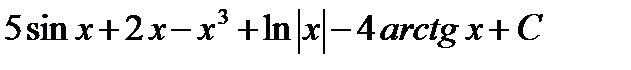
в) Интеграл табличный, поэтому можно переходить к непосредственному вычислению
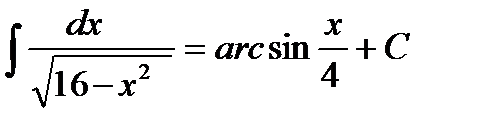
г) Интеграл не табличный, поэтому преобразуем его. Так как 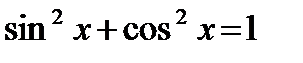 , то умножив подынтегральное выражение на
, то умножив подынтегральное выражение на 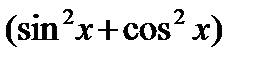 , получим
, получим
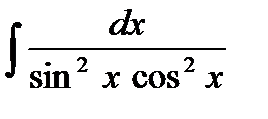 =
= 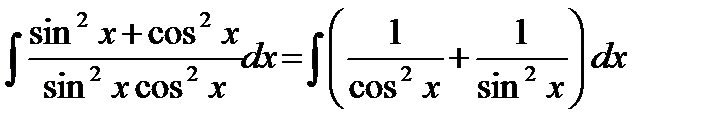 =
= 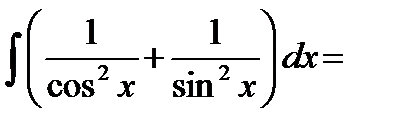
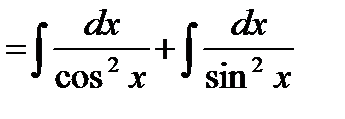 =
= 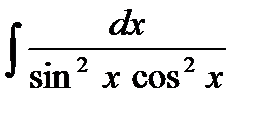 =
= 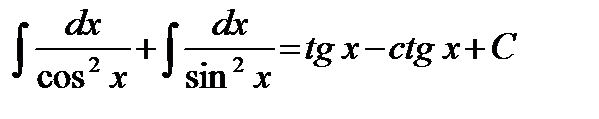
д) Сделаем подстановку 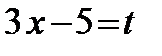 . Найдем дифференциал от обеих частей подстановки:
. Найдем дифференциал от обеих частей подстановки:
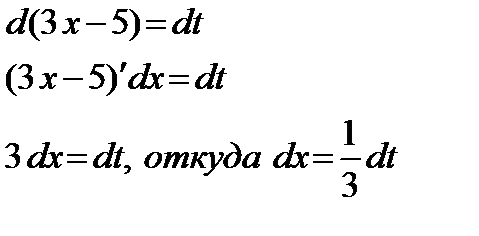
Следовательно,
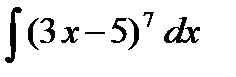 =
= 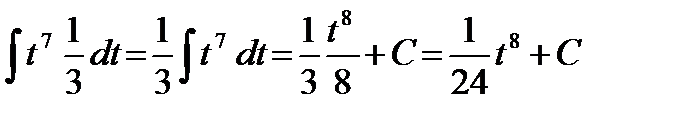
Заменив t его выражением из подстановки, получим
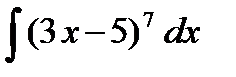 =
= 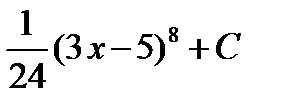
е) Полагая
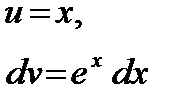 найдем
найдем 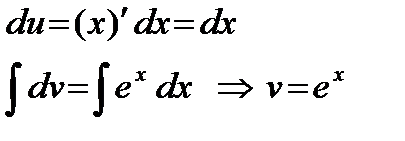
По формуле интегрирования по частям получаем:
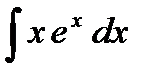 =
= 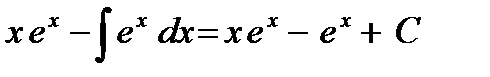
ж) Положим 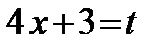 , тогда
, тогда 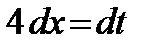 , или
, или 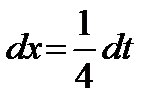 .
.
Следовательно,
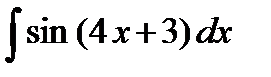 =
= 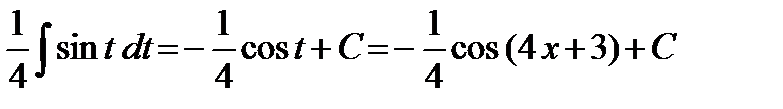

з) Положим
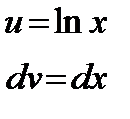
Тогда
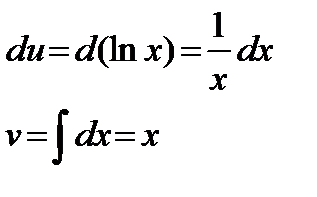
Следовательно, 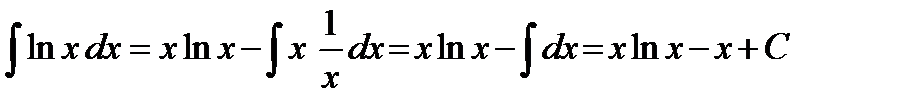
2. Вычислите определенные интегралы:
а) 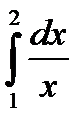 =
= 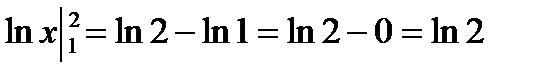
б) 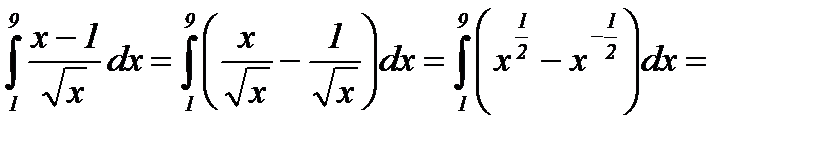
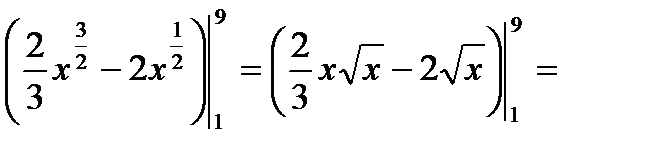
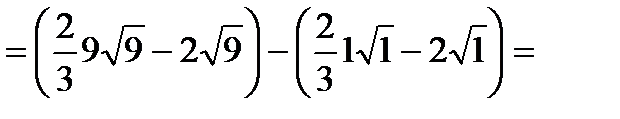
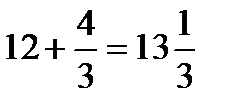 .
.
в) 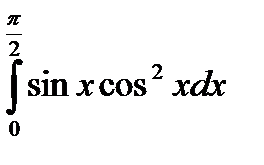 =
= 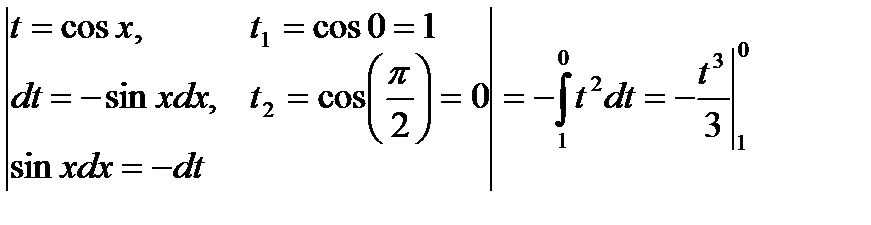
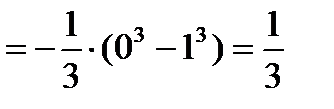 .
.
г) 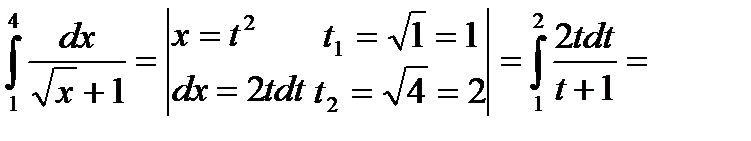
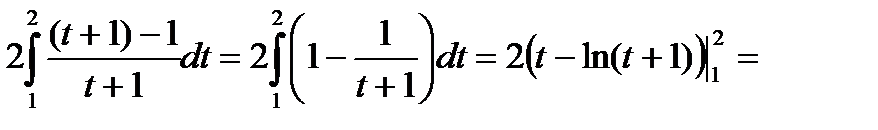
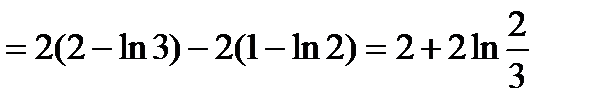 .
.
д) 
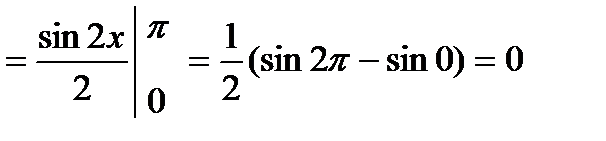 .
.
е)  =
= 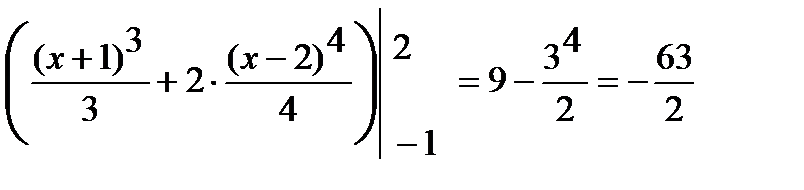 .
.
ж)
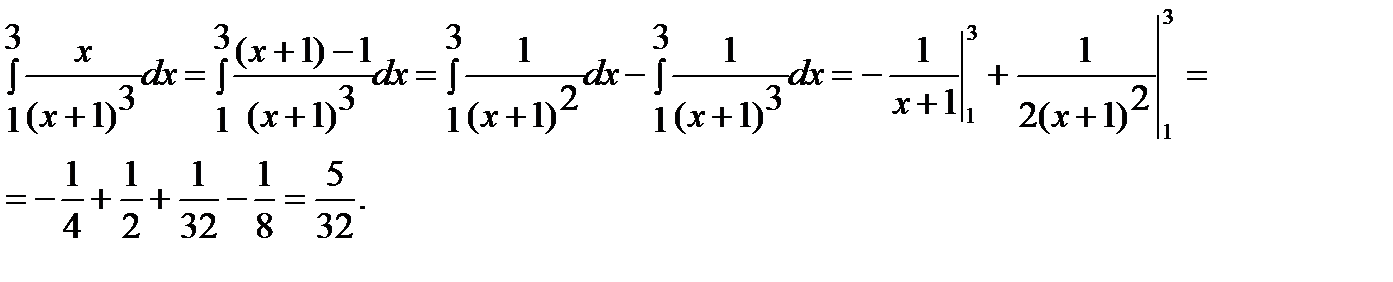
з) Применяя формулу понижения степени, получаем
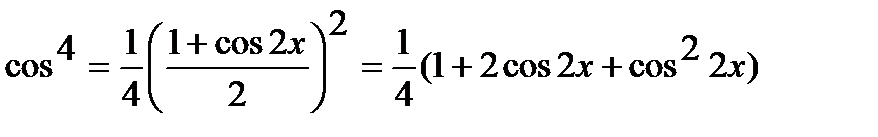 ,
,
где 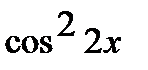 =
= 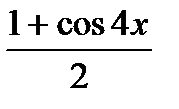 .
.
Следовательно, 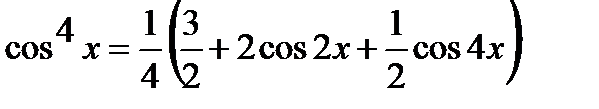 ,
,
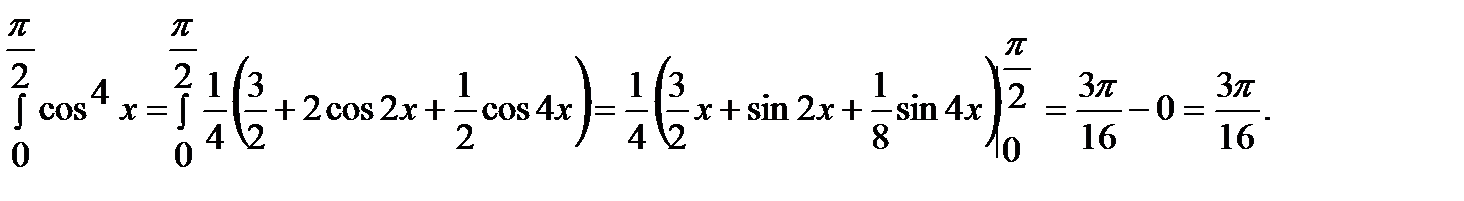
3. Вычислить площадь фигуры, ограниченной линиями:
а)  ,
, 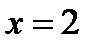 ,
,  ,
,  .
.
Построим линии, ограничивающие фигуру.
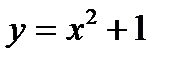 – парабола, симметричная относительно оси о у, вершина (0;1).
– парабола, симметричная относительно оси о у, вершина (0;1).
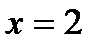 – прямая, проходящая через точку (2;0), параллельная оси о у.
– прямая, проходящая через точку (2;0), параллельная оси о у.
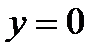 – аналитическое выражение оси о х.
– аналитическое выражение оси о х.
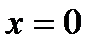 – аналитическое выражение оси о у.
– аналитическое выражение оси о у.
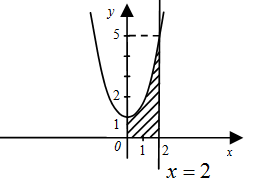
Построенная фигура является криволинейной трапецией с основанием на оси ох, поэтому её площадь вычисляется по формуле
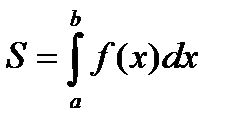 .
.
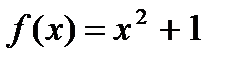 ,
, 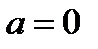 ,
, 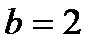 .
.
Тогда 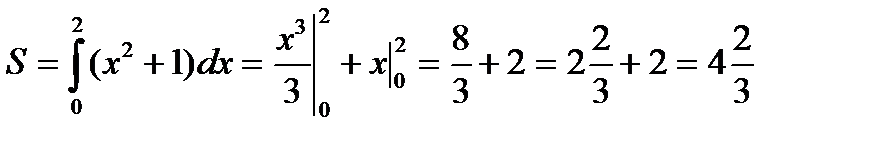 (кв. ед.).
(кв. ед.).
б) 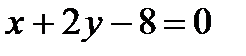 ,
, 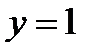 ,
, 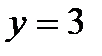 ,
, 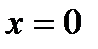 .
.
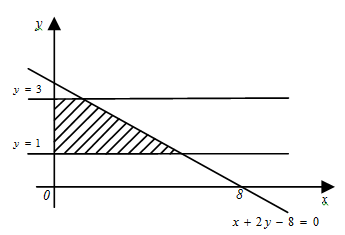
Построим линии ограничивающие фигуру.
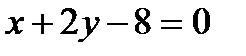 – прямая; если
– прямая; если 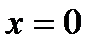 , то
, то 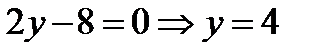 ,
,
если 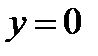 , то
, то 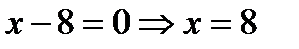 .
.
Прямая проходит через точки (0; 4), (8; 0).
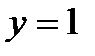 – прямая, параллельная оси о х.
– прямая, параллельная оси о х.
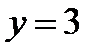 – прямая, параллельная оси о х.
– прямая, параллельная оси о х.
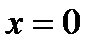 – ось о у.
– ось о у.
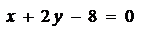
|
Фигура является криволинейной трапецией с основанием на оси о у, поэтому 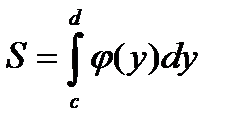 .
.
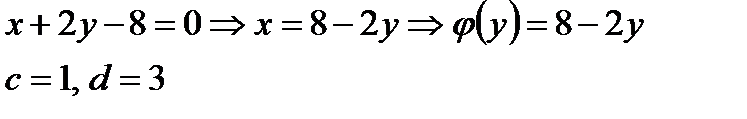
Тогда 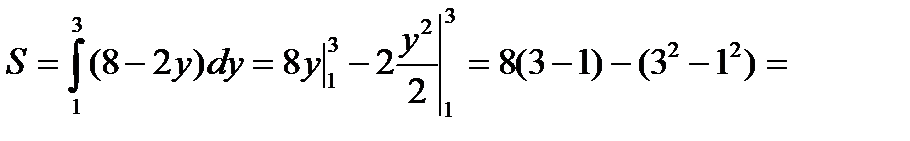
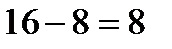 (ед2).
(ед2).
в) Вычислить площадь фигуры, ограниченной линиями
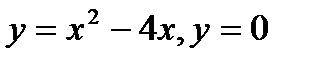 .
.
Построим линии ограничивающие фигуру.
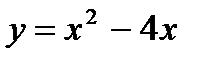 - парабола, симметричная относительно оси OY.
- парабола, симметричная относительно оси OY.
Т.к. 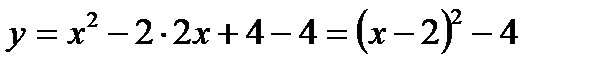 , то вершина
, то вершина 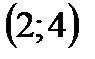 .
.
Координаты вершины также можно определить по формуле
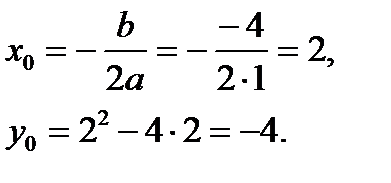
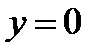 - ось OX.
- ось OX.
Найдем координаты точек пересечения графиков (рис.9) функций.
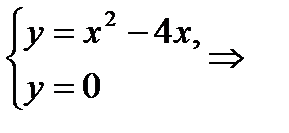
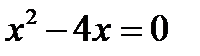
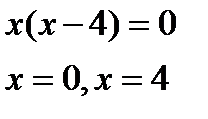
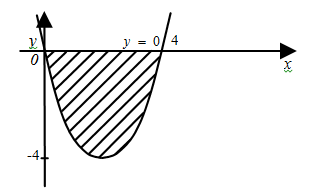
Т.о. 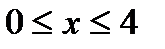 , на этом отрезке функция
, на этом отрезке функция 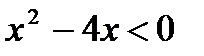 , поэтому
, поэтому 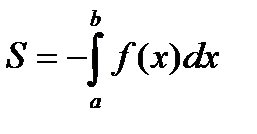 .
.
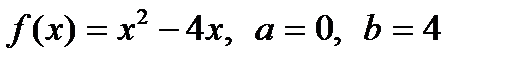 .
.
Тогда 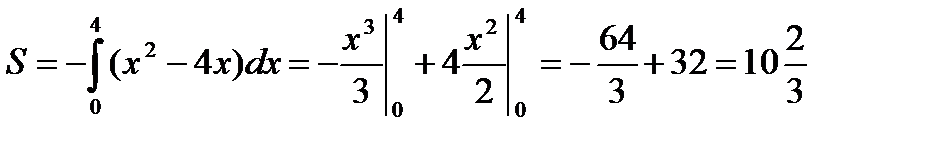 (ед2).
(ед2).
г) Вычислить площадь фигуры, ограниченной линиями
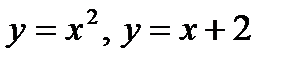
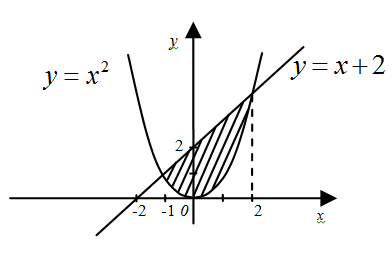
Построим линии, ограничивающие фигуру.
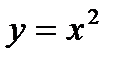 – парабола, симметричная относительно оси о у, вершина (0;0).
– парабола, симметричная относительно оси о у, вершина (0;0).
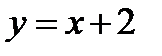 – прямая, если
– прямая, если 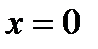 , то
, то 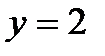 ,
,
если 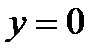 , то
, то 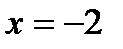 .
.
Найдём точки пересечения линий:
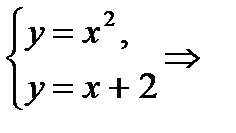
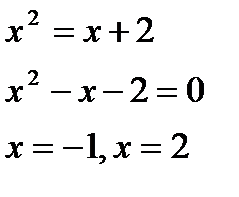
Т.о. 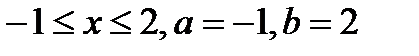
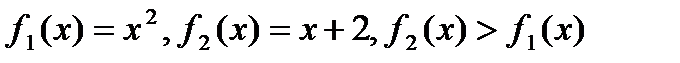 .
.
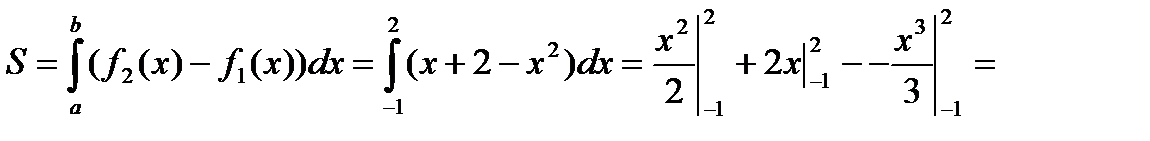
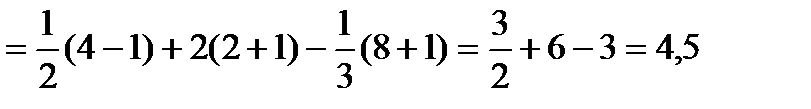 (ед2).
(ед2).
Приложение 1
к УМП по дисциплине
«____________________»
 2017-12-14
2017-12-14 815
815








