Раздел 2. Дифференциальное исчисление

Задания для самоконтроля

 

1. Вычислить производную функции:

 

а)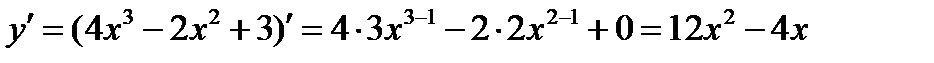

 

б)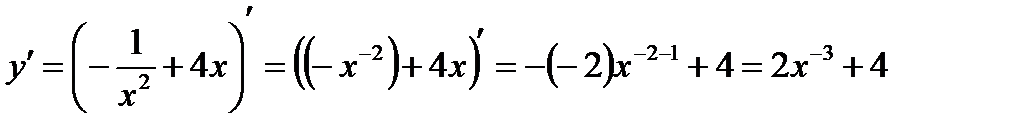

 

в)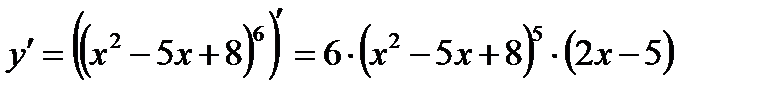

 

г)

 

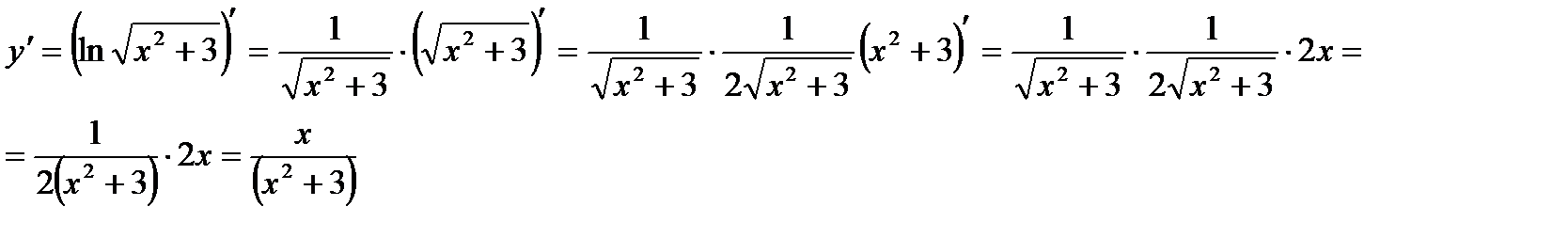
д)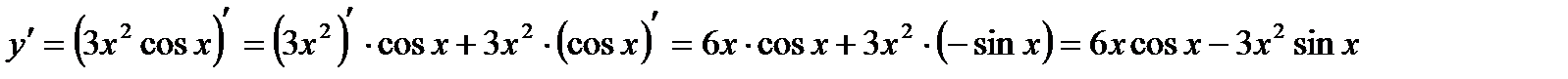

е)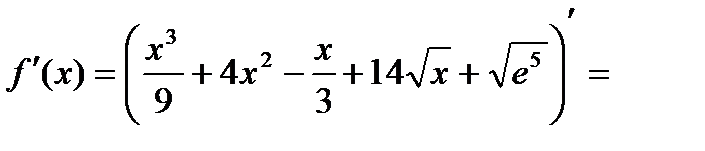

.

 

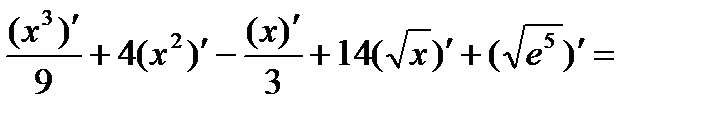
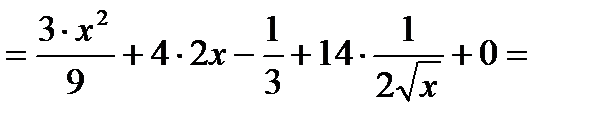
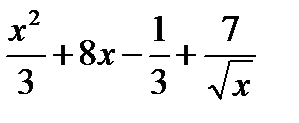ж) .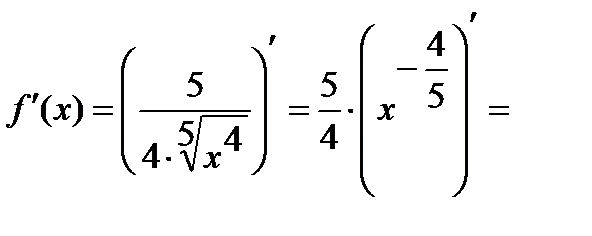

 

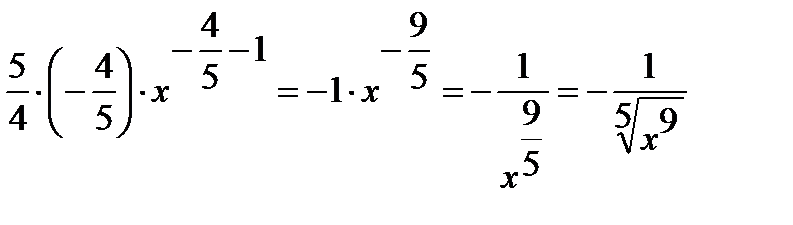з)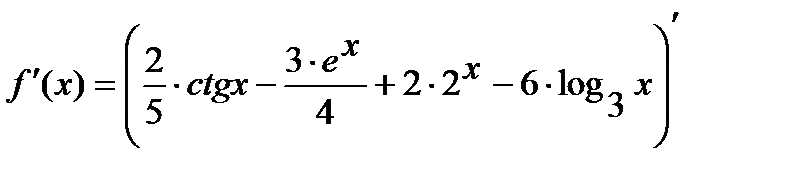

.

 

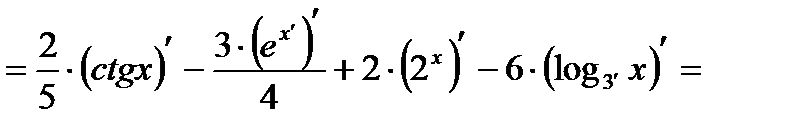
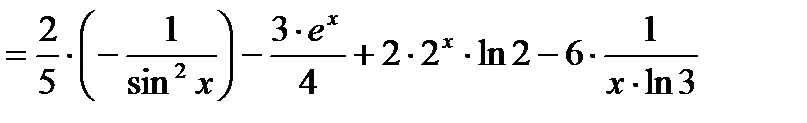
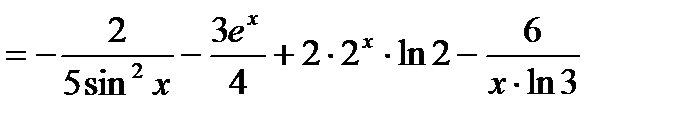и) .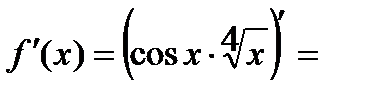

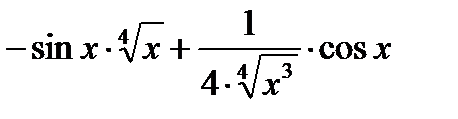
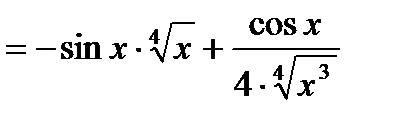к) .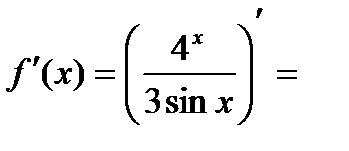

 

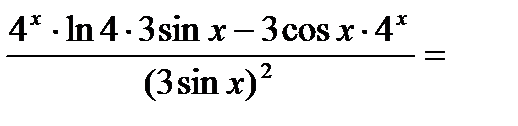
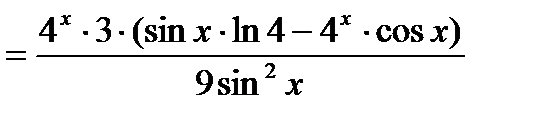
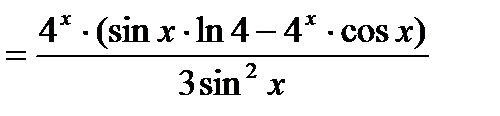л) .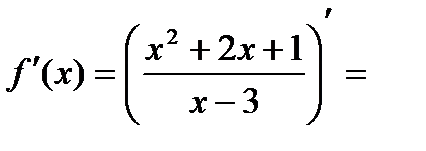

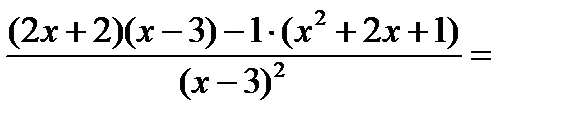
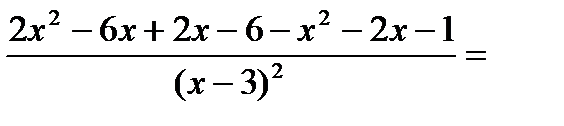
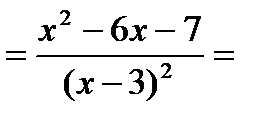
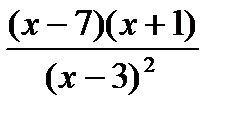м)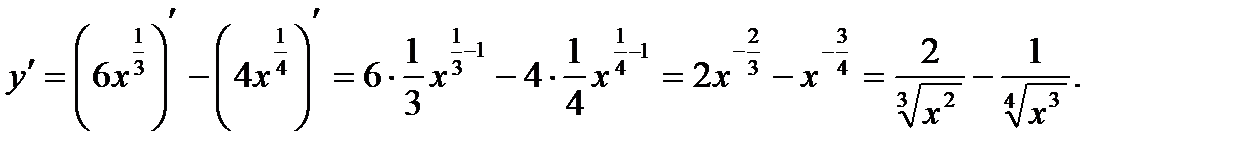

н) у = ( х ²+3)¹⁰

Это сложная функция. Пусть х ² + 3 = u, тогда у = u ¹⁰. Производная находится по формуле дифференцирования сложной функции:

у'= (u ¹⁰)'=10 u⁹u'_x,

u'_x= (x ²+3)' = 2 x,

y' =10(x ²+3)⁹2 x,

y' =20 x (x ² + 3)⁹.

о) y = sin 8 x.

Пусть 8х=u, тогда у=sinu.

y'= (sin u) '= cos u·u'_x;

u'_x =(8 x)'= 8

y' =cos u· 8или y' =8cos8 x

п) Найти производную функции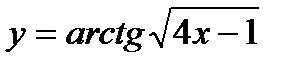

Пусть 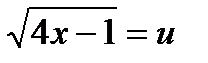, тогда 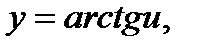и

,

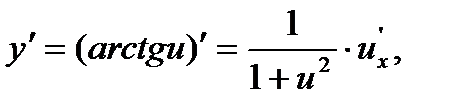
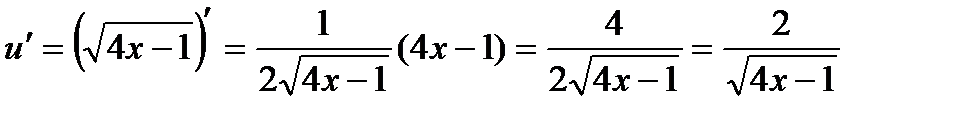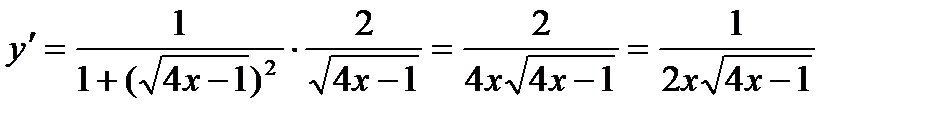
р) Продифференцировать функцию у= ln sin x

sin x = u, y = ln u, тогда

 

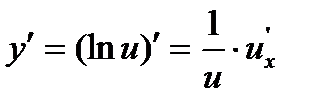
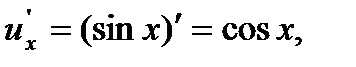
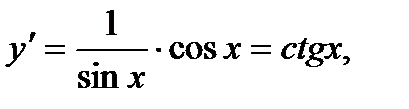
2.

а) Дана функция 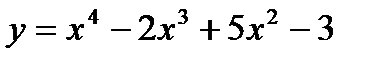. Найти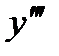

 

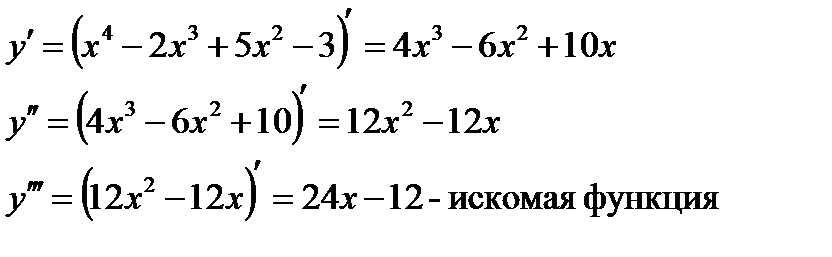
б) Дана функция 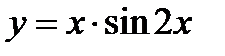. Найти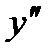

 

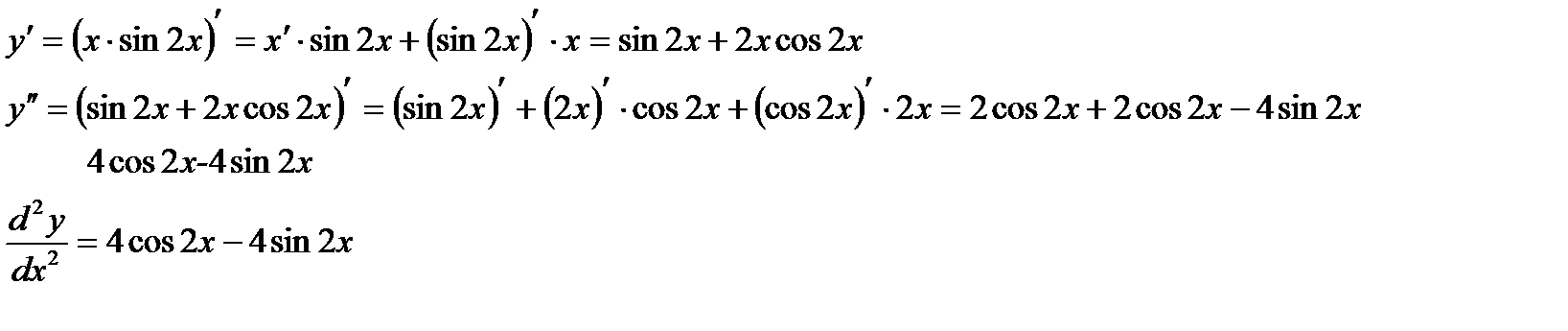
3. Составить уравнение касательной к графику функции 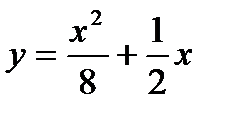, проходящей через точку х ₀=2.

 

Находим 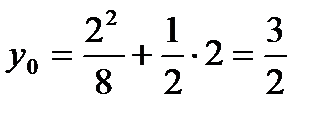, затем

 

 

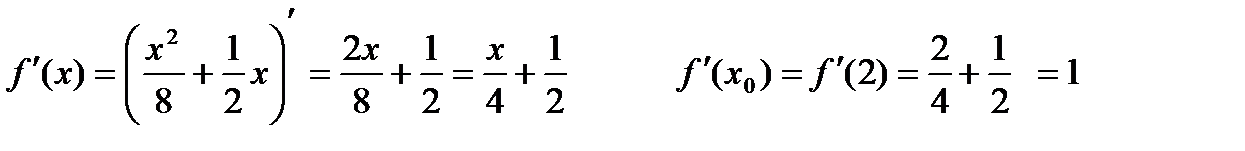
Тогда составим уравнение прямой

 

4. Исследовать функцию 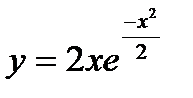и построить ее график.

Решение.

1. Область определения .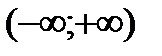

2. Функция нечетная, так как 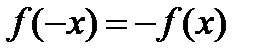и график ее симметричен относительно начала координат.

3. Вертикальных асимптот нет, так как функция определена при всех действительных значениях х.

4. Поведение функции в бесконечности:

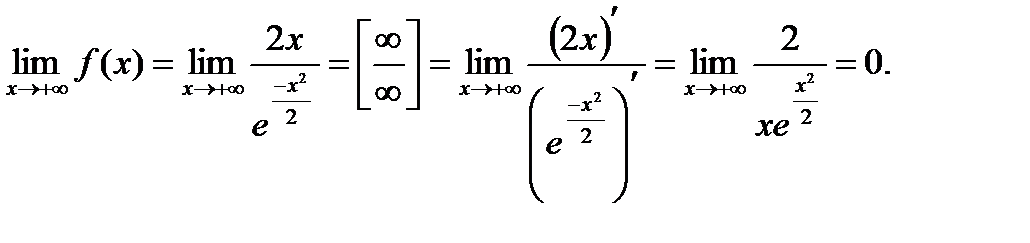
В силу нечетности функции 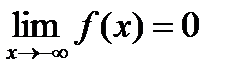, т.е. прямая у =0(ось абсцисс) – горизонтальная асимптота.

5. Экстремумы и интервалы монотонности:

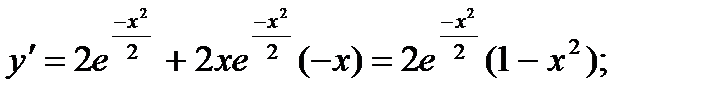
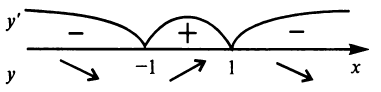
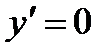при 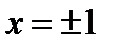, т.е. критические точки х ₁= –1, x ₂=1. Знаки производной изображены на рисунке.

 

Таким образом, х = –1 есть точка минимума; х = 1 – точка максимума и

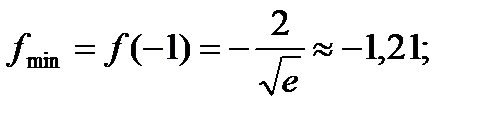
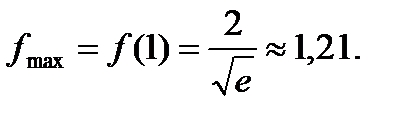
Функция убывает на интервалах 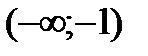и 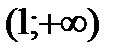и возрастает на интервале .

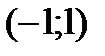6. Интервалы выпуклости и точки перегиба:

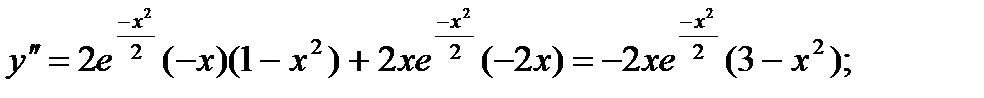
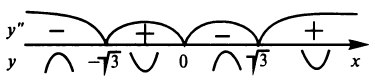
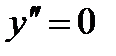при х = 0 и 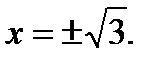Знаки второй производной изображены на рисунке14.

 

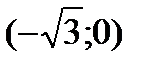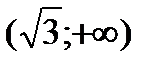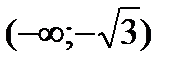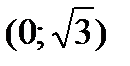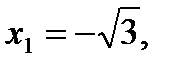
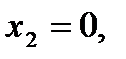
Таким образом, функция выпукла вниз на интервалах и и выпукла вверх на интервалах и , а 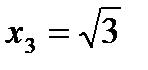– точки перегиба.

7. f (0) = 0. Уравнение f (х) = 0 имеет единственное решение х = 0, т.е. график функции пересекает оси в начале координат (0; 0).

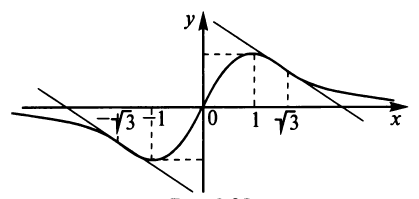
График функции изображен на рисунке.