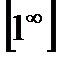Вычислить пределы
а) 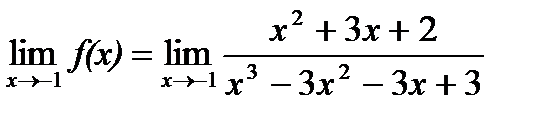 .
.
 .
.
Функция f(x) непрерывна в точке x = –1, 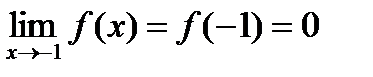 .
.
Ответ: 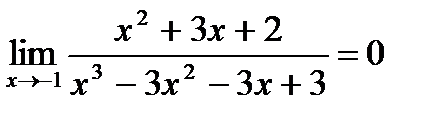 .
.
б)  .
.
 .
.
Введем новую переменную t = x –(–1) = x +1, при x → –1 t →0, x = t – 1.
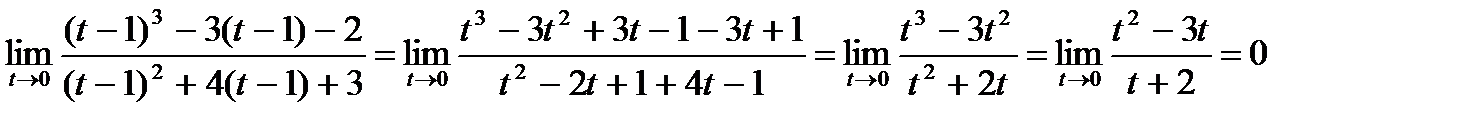
Ответ: 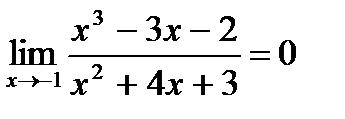 .
.
в)  .
.
 .
.
Введем новую переменную t = x –π, t →0, x = t +π.
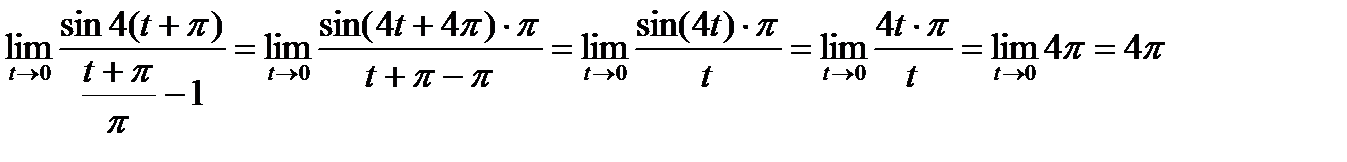 .
.
Ответ: 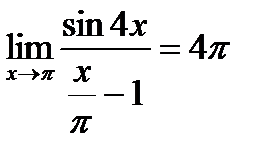 .
.
г) 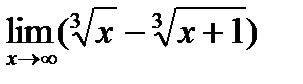 .
.
Неопределенность вида 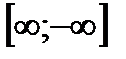 . Выносим бесконечно большую величину x под корнем.
. Выносим бесконечно большую величину x под корнем.

Ответ:  .
.
д) 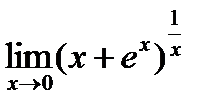

Ответ: 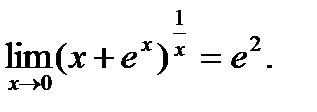
е)  .
.
Неопределенность вида  .
.
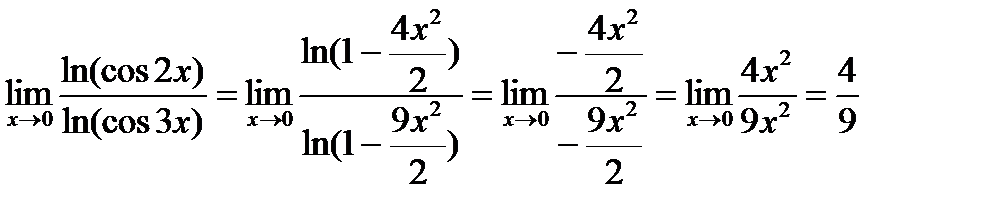
Ответ: 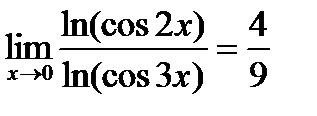 .
.
ж) 
Применить теорему о пределе дроби (частного) нельзя, т.к. при х ®0
lim (5 х 3 – 3 х 2)=0
До перехода к пределу следует упростить данную дробь:
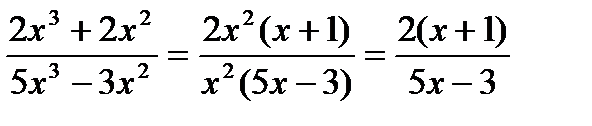
Предел знаменателя
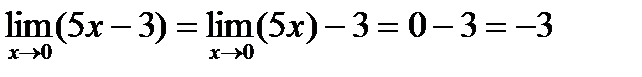 -3 ¹ 0
-3 ¹ 0
Применяя теперь теорему о пределе дроби (частного), получим:
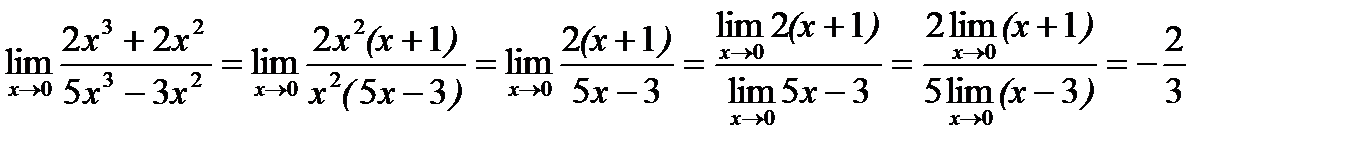
Ответ: 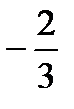
з) 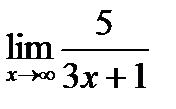
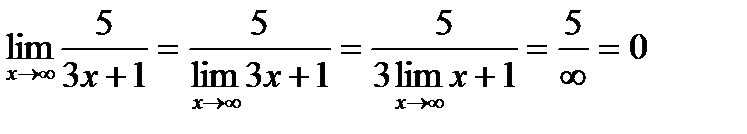
Ответ: 0.
и) Найти 
Числитель и знаменатель дроби превращаются в бесконечность, а их отношение не имеет смысла. Поэтому преобразуем дробь, разделив числитель и знаменатель дроби на наивысшую степень аргумента, т.е. на х3.
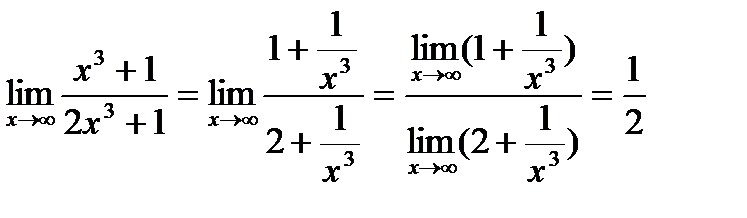
Ответ:  .
.
к) 
Применить теорему о пределе дроби нельзя, т.к. предел знаменателя равен нулю.
Перепишем данное выражение так:
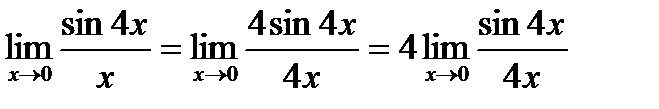 .
.
Применяя формулу 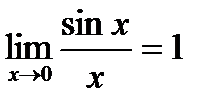 ,
,
получим: 
Ответ: 4.
л) 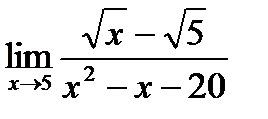
Решение. применить теорему о пределе частного нельзя, т.к. при х =5 числитель и знаменатель обращаются в нуль. Перепишем данную дробь в виде
 ,
,
Переходя к пределу, получим:
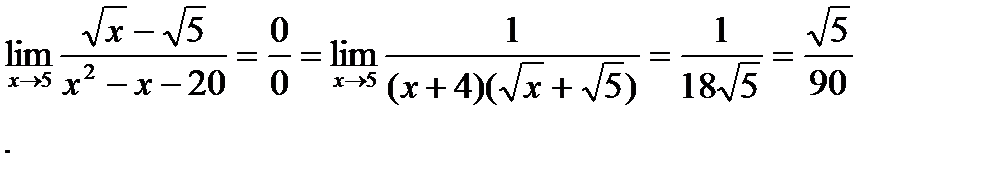
Ответ. 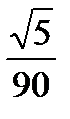
м) 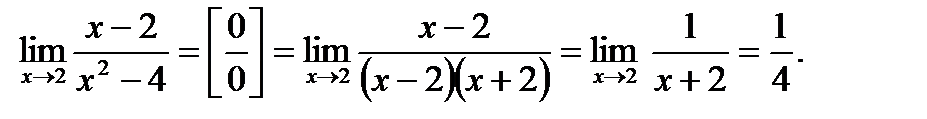
н) 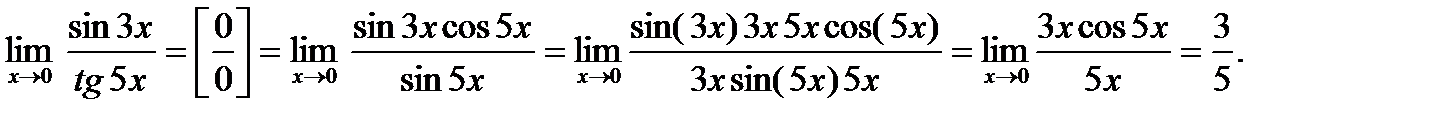
о) 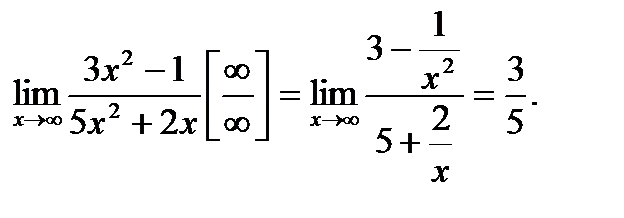
п) 
р) 
2. Исследовать непрерывность в точке х = 0 заданной функции: 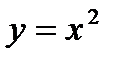 .
.
Решение:

В точке x =0 функция y = f (x) непрерывна, так как выполнены все три условия непрерывности 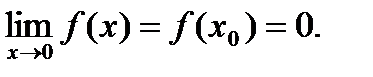
3. Исследовать функцию 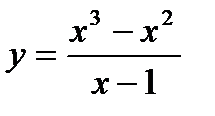 на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1) Под прицел попадает единственная точка 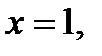 в которой функция не определена.
в которой функция не определена.
2) Вычислим односторонние пределы:

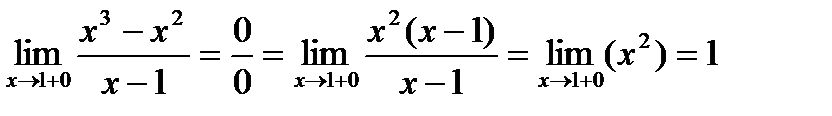
Односторонние пределы конечны и равны.
Таким образом, в точке  функция терпит устранимый разрыв.
функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение 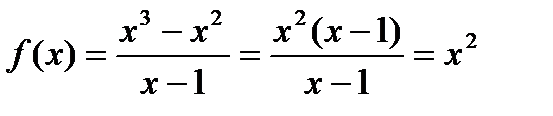 и вроде бы получается обычная парабола. но исходная функция не определена в точке
и вроде бы получается обычная парабола. но исходная функция не определена в точке  , поэтому обязательна следующая оговорка:
, поэтому обязательна следующая оговорка:
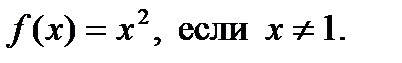 ,
,
Выполним чертёж:
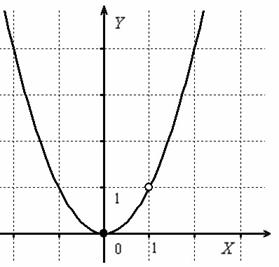
Ответ: функция непрерывна на всей числовой прямой кроме точки  , в которой она терпит устранимый разрыв.
, в которой она терпит устранимый разрыв.
 2017-12-14
2017-12-14 2937
2937