Оглавление
Введение. 8
Модель Андерсона уединенной примеси. 12
Случай нескольких самосогласованных решений. 17
Заключение. 26
Список литературы.. 27
Приложение. 28
Введение
За магнитные свойства твердых тел отвечают магнитные моменты содержащихся в них электронов. В зависимости от состояния, в котором находится твердое тело, электроны могут вести себя по-разному [1]. В диэлектриках все электроны локализованы на соответствующих атомах. В металлах и сплавах электроны могут свободно перемещаться по кристаллу. Это означает, что атомы в кристалле расположены настолько близко друг к другу, что их внешние незаполненные электронные оболочки перекрываются и расположенные на них электроны перестают быть связанными с отдельными атомами и коллективизируются. Этим и обусловлена высокая проводимость таких веществ. В простейшем классическом приближении, металл рассматривается как решетка из ионов, а электроны проводимости – как газ свободных, невзаимодействующих электронов. Однако в 1928 году В. Паули было показано, что классический подход не подходит для описания электронного газа в металле, так как он не учитывает взаимодействие между электронами. Он показал, что электроны являются квантовыми объектами, которые подчиняются статистике Э. Ферми. Именно квантовый характер электронов, и в частности наличие у них спина, обуславливает магнитные свойства металлов.
Магнетики с коллективизированными электронами представляют собой довольно широкий класс веществ, имеющих большое прикладное значение [2,3]. В частности, к ним относятся все переходные металлы группы железа. Примерами таких систем, в которых за магнитные свойства отвечают коллективизированные электроны являются металлические магнитные сверхрешетки с гигантским магнетосопротивлением, кластеры на металлической поверхности, обменно-связанные слои жестких и мягких магнетиков, называемые спиновыми пружинами.
Сверхрешетка — это слоистый кристалл, состоящий из строго чередующихся слоев магнитного и немагнитного материала толщиной всего в несколько атомов. Приставка «сверх» отражает здесь наличие периодической структуры большего размера, чем период кристаллической решетки. Если слои ферромагнетика (железа, Fe) чередуются с тонкими слоями немагнитного металла (хрома, Cr) определенной толщины, то слои ферромагнетика будут чередовать направление намагниченности. Однако если эту структуру поместить в достаточно сильное внешнее поле, то намагниченность всех слоев развернется в одну сторону. Если поле убрать, то антиферромагнитное упорядочивание вновь восстановится. Таким образом, появилась возможность легко изменять тип магнитной упорядоченности [4,5].
Другим примером систем с коллективизированными электронами являются кластеры на металлической поверхности. В последнее время появилась возможность очень точно перемещать атомы с помощью туннельного микроскопа, тем самым, создавая кластеры заданной геометрии на поверхности. Сканирующий туннельный микроскоп представляет собой острую тонкую иглу, которую подносят к образцу на расстояние нескольких ангстрем. Если приложить к этой игле напряжение, то ближайший к ней атом образца превращается в ион и "перескакивает" на иглу. После этого слегка переместив иглу и изменив напряжение, можно заставить этот атом перейти обратно на поверхность образца. Таким образом, можно манипулировать атомами и создавать кластеры атомного масштаба.
Обычно переход из магнитного состояния в немагнитное представляет собой фазовый переход второго рода. При таких переходах термодинамические потенциалы непрерывны, а их производные имеют особенности и расходимости. Однако в ряде магнитоупорядоченных систем возможен магнитный фазовый переход первого рода. В этом случае при достижении определенной критической температуры, называемой точкой Кюри, магнитный момент скачком уменьшается до нуля. Такой переход был обнаружен в сплаве MnAs и некоторых других. Помимо переходов типа порядок – беспорядок в магнитоупорядоченных веществах могут быть магнитные переходы типа порядок – порядок (например, ферромагнетизм – антиферромагнетизм). В зависимости от резкости перехода они могут быть переходами 1-го или 2-го рода.
Механизм возникновения магнитных моментов в системе коллективизированных электронов (так называемый механизм Стонера) состоит в следующем. Обменное взаимодействие приводит к тому, что энергетические зоны для электронов с разными проекциями спина сдвигаются друг относительно друга по шкале энергий на некоторое расстояние. Энергия электронов со спином, направленным по полю уменьшается, а энергия со спином, направленным против поля увеличивается, и часть электронов перейдет из энергетически невыгодной зоны в энергетически выгодную. Таким образом, появляется магнитный момент, определяемый разностью числа электронов в подзонах:
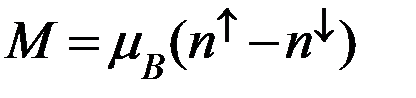
Необходимым условием возникновения ферромагнетизма является достаточно большая плотность энергетических состояний вблизи уровня Ферми 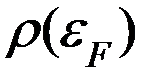 , т.е. выполнение критерия Стонера:
, т.е. выполнение критерия Стонера:
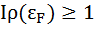 ,
,
где I- коэффициент обменного взаимодействия.
Это условие выполняется в 3d-металлах группы железа (железо, никель, кобальт и т.д.), где происходит заполнение 3d-оболочки, когда 4s-оболочка уже частично заполнена. Тем самым образуется система коллективизированных электронов, состоящая и 3d-электронов и 4s-электронов внешних слоев. Плотность состояний вблизи уровня Ферми получается достаточно высокой для выполнения критерия Стонера и в металле возникает ферромагнитное упорядочение.
Теория Стонера носит феноменологический характер. В данной работе для описания механизма формирования магнитных моментов в 3d-металлах используется микроскопическая модель Андерсона. В своей статье [6] Андерсон предложил модель для объяснения возникновения магнитных моментов на примесных атомах 3d элементов, помещенных в матрицу немагнитного металла. Примесные атомы не взаимодействовали друг с другом, находясь на большом расстоянии. В модели Андерсона плотность состояний для электронов с каждой из проекций спина имеет вид лоренцевского контура. В этом случае возможно существование только одного магнитного решения с отличным от нуля магнитным моментом. Для описания массивного образца используют периодическую модель Андерсона, в которой атомы, содержащие 3d-электроны, расположены в узлах кристаллической решетки и электроны, локализованные на них, могут взаимодействовать друг с другом. В этом случае на языке операторов рождения- уничтожения необходимо учитывать перескоки электронов с атома на атом. Плотность состояний, может иметь вид двух или большего числа лоренцевских контуров, отстающих друг от друга на расстояние, зависящее от параметра перескока электронов между соседними атомами. В этом случае, возможно несколько магнитных решений с разными моментами.
В настоящее время теория магнитных свойств малых кластеров активно развивается. Однако, практически во всех работах, где проводится самосогласованный расчет магнитной и электронной структуры, не проверяется, является ли данное магнитное решение единственным и, если нет, наиболее энергетически выгодным. В данной работе рассматривается решение самосогласованных уравнений для функций Грина d-электронов металлов с объемно-центрированной кубической (ОЦК) решеткой. Будет показано, что для одного и того же числа электронов возможно несколько магнитных решений. Были разработаны алгоритмы самосогласованных расчетов магнитных моментов, позволяющих анализировать случаи существования нескольких решений. Это позволяет провести расчеты магнитных моментов и энергий системы коллективизированных электронов при различных значениях параметров модели и, исходя из полученных данных, построить зависимости магнитного момента от числа частиц и энергии от числа частиц. Так как магнитные решения обладают близкими энергиями, то путем каких-либо внешних воздействий (изменение давления, температуры и т.д.) можно переводить систему в другое магнитное состояние. Таким образом, фазовые диаграммы, которые будут построены в ходе работы, позволяют предсказывать изменения магнитных свойств сплава при изменении числа электронов в нем.
Работа состоит из нескольких частей. В первой части будет дано описание периодической модели Андерсона и решения уравнения Шредингера методом функции Грина, рассмотрен случай одной примеси, описанный Андерсоном ранее. Во второй части описан случай нескольких самосогласованных магнитных решений, описан алгоритм работы программы для построения всех магнитных решений. В третьей части будут представлены результаты работы программы, построены графики зависимости магнитного момента от числа электронов и энергии состояния от числа электронов для разных значениях параметров модели.
Модель Андерсона уединенной примеси
Модель Андерсона – это модель, которая описывает микроскопический механизм возникновения локализованных магнитных моментов на примесных атомах переходных металлов в немагнитной матрице [6-8]. Для записи гамильтониана модели используется метод вторичного квантования. Суть метода вторичного квантования в том, что вместо волновых функций частиц в координатном или импульсном представлении вводятся волновые функции в представлении чисел заполнения различных состояний одной частицы. Переходы между различными состояниями одной частицы при этом описываются как уменьшение числа заполнения, соответствующего одной волновой функции, на единицу, и увеличение числа заполнения другого состояния на единицу.
Гамильтониан модели, записанный в представлении вторичного квантовании, имеет вид:
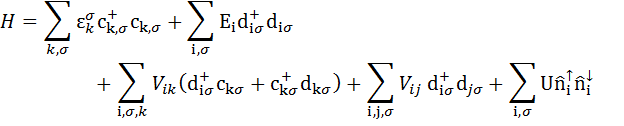
Здесь 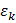 – энергия электрона с квазиимпульсом
– энергия электрона с квазиимпульсом 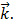 Оператор
Оператор  (
(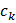 ) создает (уничтожает) электрон в зоне проводимости с квазиимпульсом
) создает (уничтожает) электрон в зоне проводимости с квазиимпульсом 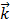 , а
, а 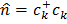 – оператор числа частиц. Таким образом первый элемент гамильтониана есть энергия электронов s-зоны. Если схематично изобразить плотность состояний (рис. 1) то первый элемент дает широкую s-зону. Аналогично вводится вторая сумма для d-электронов, которая дает узкую d-зону (Рис. 1.). Следущее слагаемое – это так называемый член sd-гибридизации. Он соответсвует переходу электрона из состояния, локализованного в d-зоне, в зону проводимости и наоборот. При учете sd-гибридизации d-зона примеси расширяется (Рис. 2.). Здесь
– оператор числа частиц. Таким образом первый элемент гамильтониана есть энергия электронов s-зоны. Если схематично изобразить плотность состояний (рис. 1) то первый элемент дает широкую s-зону. Аналогично вводится вторая сумма для d-электронов, которая дает узкую d-зону (Рис. 1.). Следущее слагаемое – это так называемый член sd-гибридизации. Он соответсвует переходу электрона из состояния, локализованного в d-зоне, в зону проводимости и наоборот. При учете sd-гибридизации d-зона примеси расширяется (Рис. 2.). Здесь 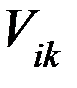 – матричный элемент перескока электрона из одной зоны в другую. Четвертая сумма описывает перескоки электронов с узла с номером i на узел с номером j. Тогда плотность состояний, при учете d-d-взаимодействия, будет иметь вид двух лоренцевских контуров, расположенных, в случае ОЦК решетки, на расстоянии
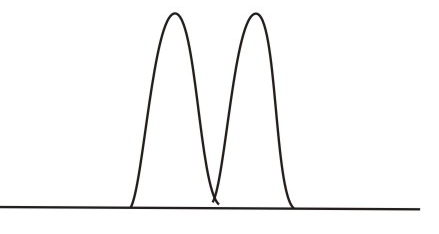
– матричный элемент перескока электрона из одной зоны в другую. Четвертая сумма описывает перескоки электронов с узла с номером i на узел с номером j. Тогда плотность состояний, при учете d-d-взаимодействия, будет иметь вид двух лоренцевских контуров, расположенных, в случае ОЦК решетки, на расстоянии 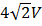 друг от друга. И последнее слагаемое – это кулоновское взаимодействие между электронами с противопложно направленными спинами. Здесь U – внутриатомное кулоновское отталкивание. Именно это член играет принципиальную роль в возникновении магнитных моментов. Под действием кулоновского отталкивания, подзоны для соответсвующих спинов сдвигаются друг относительно друга, причем одна из подзон, лежащяя ниже уровня Ферми является более заполненной, а другая, лежащая выше уровня Ферми, является более пустой (Рис. 4.). При этом в процессе самосогласования может получиться несколько магнитных решений.
друг от друга. И последнее слагаемое – это кулоновское взаимодействие между электронами с противопложно направленными спинами. Здесь U – внутриатомное кулоновское отталкивание. Именно это член играет принципиальную роль в возникновении магнитных моментов. Под действием кулоновского отталкивания, подзоны для соответсвующих спинов сдвигаются друг относительно друга, причем одна из подзон, лежащяя ниже уровня Ферми является более заполненной, а другая, лежащая выше уровня Ферми, является более пустой (Рис. 4.). При этом в процессе самосогласования может получиться несколько магнитных решений.
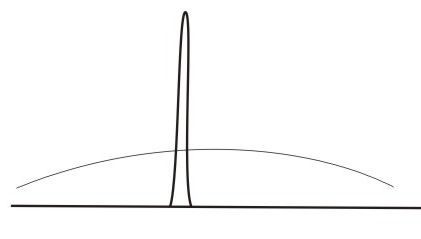 | 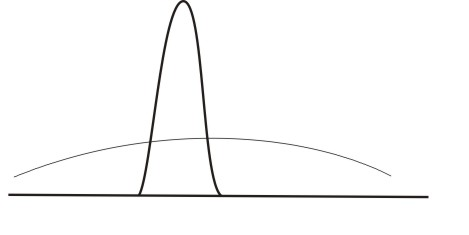 |
| Рис. 1. Плотность состояний для s и d электронов | Рис. 2. Плотность состояний при учете sd-гибридизации |
 | 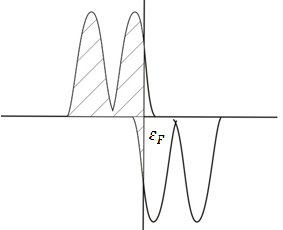 |
| Рис. 3. Плотность состояний при учете d-d-взаимодействия | Рис. 4. Плотность состояний при учете кулоновского отталкивания электронов с разными спинами. |
Впервые модель была введена Андерсоном, когда он рассматривад случай уединенной примеси, в которой отсутствовало d-d-взаимодействие,т.е. коэффециенты перескоков 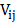 были равны нулю. Для нахождения решения такой модели Андерсон использовал метод функции Грина для уравнения Шредингера для фермионов:
были равны нулю. Для нахождения решения такой модели Андерсон использовал метод функции Грина для уравнения Шредингера для фермионов:
Физический смысл функции Грина состоит в следующем. Она представляет собой пропагатор, т.е. амплитуду вероятности того, что если в момент 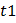 в систему в основном состоянии добавлена частица в точку r 1, то в момент t2>t1 система будет находиться в состоянии с частицей в точке r 2. Одним из методов нахождения функции Грина является построение цепочки дифференциальных уравнений. При этом в общем случае при учете кулоновского взаимодействия оказывается, что одночастичная функция Грина выражается через двухчастичную. Уравнение для двухчастичной функции Грина содержит трехчастичную и т.д. Обычно эту цепочку разрывают, предполагая, например, что двухчастичная функция выражается через произведение одночастичных и решая уравнение для одночастичной функции Грина. Чтобы найти решение такой модели, Андерсон использовал приближение Хартри-Фока. Основная идея такого подход заключается в том, что каждый электрон двигается в некотором усредненном поле, создаваемом всеми остальными электронами. В этом приближении оператор числа частиц в последнем слагаемом заменяется средним числом частиц:
в систему в основном состоянии добавлена частица в точку r 1, то в момент t2>t1 система будет находиться в состоянии с частицей в точке r 2. Одним из методов нахождения функции Грина является построение цепочки дифференциальных уравнений. При этом в общем случае при учете кулоновского взаимодействия оказывается, что одночастичная функция Грина выражается через двухчастичную. Уравнение для двухчастичной функции Грина содержит трехчастичную и т.д. Обычно эту цепочку разрывают, предполагая, например, что двухчастичная функция выражается через произведение одночастичных и решая уравнение для одночастичной функции Грина. Чтобы найти решение такой модели, Андерсон использовал приближение Хартри-Фока. Основная идея такого подход заключается в том, что каждый электрон двигается в некотором усредненном поле, создаваемом всеми остальными электронами. В этом приближении оператор числа частиц в последнем слагаемом заменяется средним числом частиц:
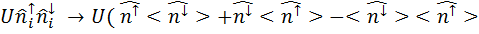 )
)
Подставим это приближение в формулу для гамильтониана:
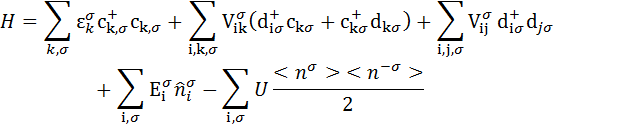
, где 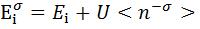
Тогда уравнение для функции Грина в матричном виде будет:
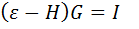 , где
, где 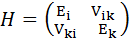
Находим из системы уравнений диагональные матричные элементы функции Грина:
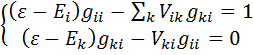 ,
, 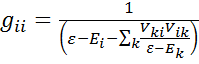
Получившейся функция Грина может рассматриваться как комплексная функция комплексного аргумента e, через мнимую часть от которой вблизи вещественной оси выражается плотность d-электронных состояний. Действительно, в общем случае плотность состояний представляет собой сумму δ-функций:
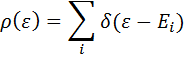
Где суммирование ведется по всем квантовым состояниям системы и в случае непрерывного спектра сумма переходит в интеграл
Рассмотрим мнимую часть функции Грина для системы с одним состоянием с энергией Е:
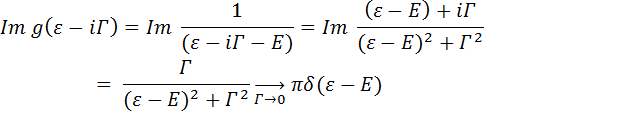
Тогда плотность состояний для электронов с проекцией спина σ в модели уединенной примеси представляет собой лоренцевский контур с шириной равной 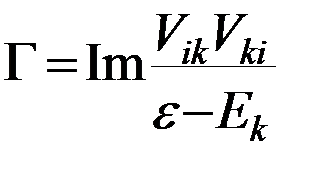
Для d-электронов с проекцией спина имеем
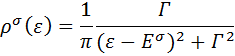
где 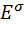 - энергия электронов с проекцией спина
- энергия электронов с проекцией спина 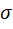
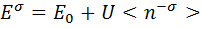 (1)
(1)
Чтобы найти число электронов проинтегрируем плотность состояний:
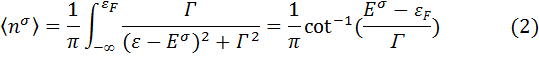
Для удовлетворения условий самосогласования необходимо решить систему:
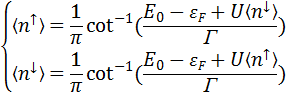
Здесь для замыкания уравнений для чисел заполнения используется выражение для энергии (1). Таким образом, задача сводится к нахождению точек пересечения графиков функций 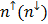 и
и 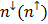 . Андерсон показал, что в зависимости от параметров модели, возможны либо одно немагнитное решение (рис. 5б), когда
. Андерсон показал, что в зависимости от параметров модели, возможны либо одно немагнитное решение (рис. 5б), когда 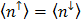 , либо три решения, одно из которых также немагнитное (рис. 5а.).
, либо три решения, одно из которых также немагнитное (рис. 5а.).
Рис. 5. График самосогласованных решений для чисел заполнения с параметрами:
а) 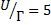 , (
, (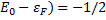 ; б)
; б) 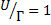 , (
, (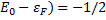
 2017-10-31
2017-10-31 862
862







