Задачи для самостоятельного решения. 1. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью

1. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

2. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.

3. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определить кинетическую энергию через 4 с после начала действия силы.

4. Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определить: а) момент сил торможения; б) момент инерции вентилятора.

5. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н·м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с².

6. С наклонной плоскости, составляющей угол 30⁰ с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.

7. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с². Определить: а) момент инерции вала; б) массу вала.

8. Горизонтальная платформа массой 25 кг и радиусом 0,8 м вращается с частотой 18 об/мин. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5 кг·м² до 1 кг·м².

9. Человек массой 60 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 об/мин, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить, с какой частотой будет тогда вращаться платформа.

10. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

3. Закон сохранения момента импульса

Анализируя уравнение моментов относительно произвольного центра и неподвижной оси, мы говорили уже об условиях, при которых момент импульса системы не будет меняться во времени.

Сформулируем эти условия ещё раз, собрав их воедино:

1. Момент внутренних сил, действующих в системе, равен нулю. Поэтому внутренние силы и их моменты не могут привести к изменению момента импульса системы.

2. Если система замкнута, то есть отсутствуют внешние силы, то момент импульса такой системы не меняется. Это закон сохранения момента импульса замкнутой системы.

3. Система может быть и незамкнутой, но если суммарный момент внешних сил, действующих на систему, равен нулю, то момент импульса такой системы остаётся постоянным во времени.

4. Если момент внешних сил относительно некоторой оси равен нулю, то момент импульса системы относительно этой оси сохраняетсянеизменным. При этом момент внешних сил относительно других направлений может и отличаться от нуля. Это будет означать, что момент импульса системы относительно этих направлений будет меняться во времени.

Лекция 9 «Механика твердого тела»

План лекции

1. Модель твердого тела в механике. Поступательное и вращательное движение твердого тела.

2. Основное уравнение динамики вращательного движения вокруг неподвижной оси.

3. Момент инерции тела. Теорема Гюйгенса-Штейнера. Примеры вычисления моментов инерции тел.

1. Модель твердого тела в механике. Поступательное и вращательное движение твердого тела

Все тела под действием приложенных сил деформируются, то есть в большей или меньшей степени меняют свою форму и размеры. Если эти деформации незначительны и не оказывают влияния на движение тела, то в механике ими пренебрегают и говорят о движении абсолютно твёрдого тела. При движении такого тела принимается, что расстояние между двумя любыми его точками не меняется. Это означает, что движение частиц твёрдого тела закономерно и определённым образом связаны друг с другом.

Любое движение твёрдого тела может быть представлено суперпозицией двух движений — поступательного и вращательного. Проиллюстрируем это утверждение простым примером (рис. 9.1). Пусть треугольник ABC в произвольном движении перемещается в положение A₁B₁C₁. Можно представить, что это перемещение происходит в два этапа. Сначала треугольник, двигаясь поступательно, занял позицию A’B₁C’, а затем во вращательном движении вокруг оси, проходящей через B₁, занял конечное положение A₁B₁C₁.

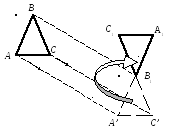
Рис. 9.1

Напомним, что поступательным движением называется движение, в котором все частицы тела за один и тот же промежуток времени получают одинаковые по величине и направлению перемещения. Это означает, что скорость и ускорение всех точек тела в этом движении одинаковы.

При вращении относительно неподвижной оси одинаков угол поворота jвсех точек тела, а, следовательно, одинаковы их угловые скорости 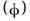и ускорения .

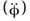Поступательное движение тела задаётся обычно уравнением движения его центра масс.

Вращательное движение описывается уравнением, которое получило название «основное уравнение динамики вращательного движения».

2. Основное уравнение динамики вращательного движения вокруг неподвижной оси

При вращении твёрдого тела относительно неподвижной оси, все точки тела движутся по плоским круговым траекториям. Выделим частицу m_i тела, вращающегося вокруг оси z (рис. 9.2). Положение частицы зададим радиус-вектором 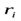относительно произвольного центра 0, лежащего на оси вращения. R_i — радиус окружности, по которой движется рассматриваемая точка. V_i =w R_i — её линейная скорость.

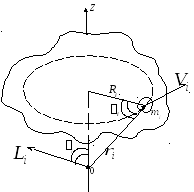
Рис. 9.2

Рассматривая твёрдое тело как неизменную систему материальных точек, для каждой из них можно записать уравнение моментов:

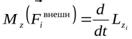. (9.1)

В левой части этого уравнения — момент внешних сил относительно оси z, действующий на частицу m_i. Справа — производная по времени проекции момента импульса частицы на ту же ось.

Момент импульса частицы относительно центра 0 (по определению) равен:

.

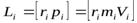Заметим, что для всех частиц 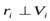, поэтому легко вычислить модуль этого вектора L_i:

L_i = m_ir_iV_i = m_ir_i w R_i.

Так как 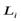образует уголa _i сосью z, то проекция этого вектора на ось z равна:

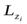= L_i Cosa _i = m_ir_i w R_i Cosa _i = m_i w R_i (r_i Cosa _i) = m_i w 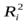. (9.2)

Учитывая этот результат, перепишем уравнение (9.1) ещё раз:

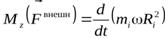. (9.3)

Подобные уравнения могут быть составлены для всех точек твёрдого тела.

Просуммировав все эти уравнения, получим закон вращательного движения твёрдого тела:

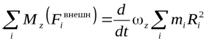
или

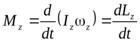. (9.4)

Здесь: M_z — суммарный момент всех внешних сил, вращающих твёрдое тело вокруг оси z;

w _z — угловая скорость вращения;

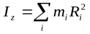— новая характеристика твёрдого тела — его момент инерции относительно оси вращения;

L_z = I_z w _z — момент импульса тела относительно оси z.

Если момент инерции твёрдого тела I_z не меняется, уравнению (9.4) можно придать такой вид:

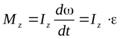. (9.5)

Здесь ε = 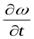— угловое ускорение вращающегося тела.

Уравнение (9.5) называется основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси.

M_z = I_z×ε (9.6)

Трудно не заметить сходство этого уравнения со вторым законом Ньютона для движения точки:

F_z = ma_z

Сравнивая эти два выражения, отметим, что в уравнении для вращательного движения в качества «силы» выступает момент силы, вместо линейного ускорения — угловое, вместо массы используется момент инерции I_z.

Сходство этих уравнений можно продолжить, записав их иначе (9.2)

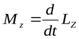
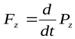
Здесь: L_z = I_z w _x — момент импульса тела относительно оси z,

P_z = mV _z— проекция вектора импульса частицы на ось z.

Во вращательном движении аналогом импульса Р является момент импульса L.

Рассмотренные аналогии позволяют назвать уравнение (9.6) уравнением второго закона динамики (Ньютона) для вращательного движения:

момент внешних сил, вращающих тело вокруг данной оси, равен моменту инерции тела относительно этой оси, умноженному на угловое ускорение тела.

Вернемся ещё раз к уравнению (9.4):

.

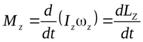Оно в равной степени справедливо как для твердого тела, так и для системы тел. Если момент внешних сил относительно оси z равен нулю, то момент импульса системы относительно этой же оси будет оставаться постоянным.

M_z = 0, Þ 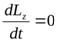Þ L_z = I_z w _z = сonst.

Это закон сохранения момента импульса — аналог закона сохранения импульса замкнутой системы. Но есть между этими законами одно существенное различие. Постоянство импульса частицы (если её масса не меняется) означает неизменность её линейной скорости:

p = mV = сonst. Þ V = сonst.

Если же не меняется момент импульса тела (L_z), то это не означает постоянства угловой скорости:

L_z = I_z w= сonst.

Изменение момента инерции вращающегося тела приведёт к изменению его угловой скорости даже в случае отсутствия внешних вращающих моментов. При этом сохранится неизменным произведение I_z ×w= сonst., то есть угловая скорость окажется обратно пропорциональной моменту инерции тела (системы):

.

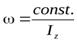Известно много примеров, иллюстрирующих эту особенность закона сохранения момента импульса: вращение фигуристов и балерин, опыты на скамье Жуковского, сальто-мортале гимнастов и т.п.

Моментом импульса относительно неподвижной оси z принято называть скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определœенного относительно произвольной точки 0 данной оси. Значение момента импульса L_z не зависит от положения точки 0 на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса 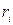с некоторой скоростью 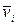. Скорость 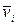и импульс 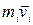перпендикулярны этому радиусу, ᴛ.ᴇ. радиус является плечом вектора 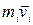. По этой причине можно записать, что момент импульса отдельной точки относительно оси z равен

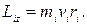
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:

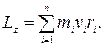
Учитывая связь между линœейной и угловой скоростями (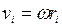), получим следующее выражение для момента импульса тела относительно неподвижной оси:

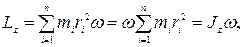(4.12)

ᴛ.ᴇ. момент импульса твердого тела относительно оси равен произведению момента инœерции тела относительно той же оси на угловую скорость.

Продифференцировав выражение (4.12) по времени, получим:

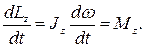(4.13)

Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всœех внешних сил, действующих на тело.

Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:

если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.

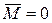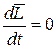Действительно, в случае если , то , откуда

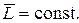(4.14)

Другими словами, момент импульса замкнутой системы с течением времени не изменяется.

Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси:

если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, ᴛ.ᴇ. если M_z =0, то 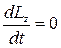, откуда

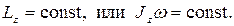(4.15)

Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, ᴛ.ᴇ. с инвариантностью физических законов относительно выбора направления осœей координат системы отсчета.

Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского принято называть горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси ОО₁. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси ОО₁ с угловой скоростью 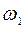. Приближая гантели к себе, человек уменьшает момент инœерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения 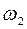возрастает. Тогда по закону сохранения момента импульса относительно оси ОО₁ можно записать:

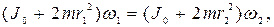(4.16)

где 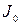- момент инœерции человека и скамьи; и 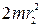- моменты инœерциигантелœей в первом и втором положениях; m – масса одной гантели; r₁, r₂ – расстояния от гантелœей до оси ОО₁.

Изменение момента инœерции системы связано с изменением ее кинœетической энергии:

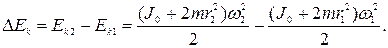
Используя выражение для 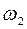, полученное из (4.16)

,

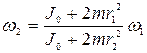после преобразований получим:

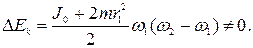
Это изменение кинœетической энергии системы численно равно работе, совершенной человеком при перемещении гантелœей.

В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.

Таблица 4.2

Поступательное движение	Вращательное движение
Масса m	Момент инœерции Jz
Скорость	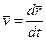Угловая скорость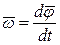
Ускорение	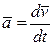Угловое ускорение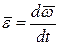
Сила	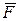Момент силы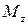
Импульс	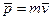Момент импульса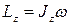
Основное уравнение динамики:	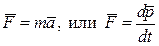Основное уравнение динамики: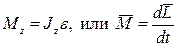
Работа	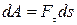Работа вращения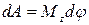
Кинœетическая энергия	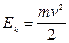Кинœетическая энергия вращения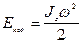

Краткие выводы

· Вращательным принято называть движение, при котором всœе точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

· Момент инœерции тела относительно оси вращения - ϶ᴛᴏ физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:

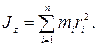
· Момент инœерции тела J_z относительно любой оси вращения равен моменту его инœерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

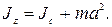
· При вращении абсолютно твердого тела вокруг неподвижной оси z его кинœетическая энергия равна половинœе произведения момента инœерции относительно оси вращения на квадрат угловой скорости:

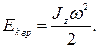
· Из сравнения формул 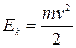и 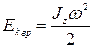следует, что момент инœерции – мера инœертности тела при вращательном движении.

· Работа вращения тела идет на увеличение его кинœетической энергии и определяется выражением 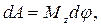где M_z – момент сил относительно оси вращения z.

· Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:

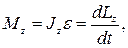
где L_z – момент импульса твердого тела относительно оси z.

· В замкнутой механической системе момент внешних сил относительно неподвижной оси M_z =0 и 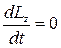, откуда L_z =const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осœей координат системы отсчета.

Вопросы для самоконтроля и повторения

1. Что принято называть моментом инœерции тела? Какова роль момента инœерции во вращательном движении?

2. Сформулируйте теорему Штейнера. От чего зависит момент инœерции тела?

3. Что принято называть моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?

4. Что такое момент импульса твердого тела? Как определяется направление момента импульса?

5. Какова формула для кинœетической энергии тела, вращающегося вокруг неподвижной оси? Как определяется работа при вращении тела?

6. Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.

7. Сформулируйте закон сохранения момента импульса. В каких системах он выполняется?

8. Сопоставьте основные величины и уравнения динамики поступательного и вращательного движений.

Примеры решения задач

Задача 1. Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии по закону 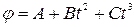, где В =2 рад/с², С =-0,5 рад/с³. Определить момент сил относительно оси вращения для момента времени t =3 c.

Дано: R =0,1 м; m =5 кг; 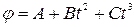рад; В =2 рад/с²; С =-0,5 рад/с³; t =3 c.

Найти: M_z.

Решение

Согласно уравнению динамики вращательного движения твердого тела относительно неподвижной оси

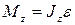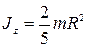, где - момент инœерции шара;

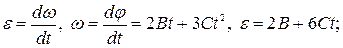
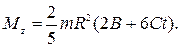
Для t =3 c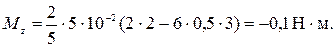

Ответ: M_z =-0,1 Н·м.

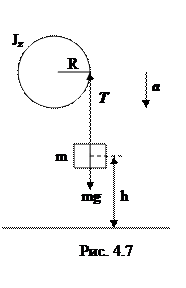Задача 2. На однородный сплошной цилиндрический вал радиусом 20 см, момент инœерции которого 0,15 кг·м², намотана легкая нить, к концу которой прикреплен груз массой 0,5 кᴦ. До начала вращения барабана высота груза над полом составляла 2,3 м (рис.). Определить: а) время опускания груза до пола; б) силу натяжения нити; в) кинœетическую энергию груза в момент удара о пол.

Дано: R =0,2 м; J_z =0,15 кг·м²; m =0,5 кг; h =2,3 м.

Найти: t, T, E_к.

Решение

По закону сохранения энергии

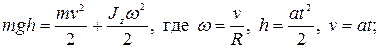
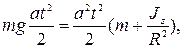откуда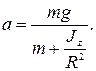

Время опускания груза до пола:

.

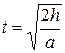Уравнение динамики вращательного движения вала 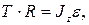откуда сила натяжения нити

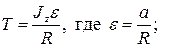тогда .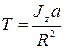

Кинœетическая энергия груза в момент удара о пол:

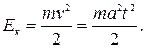
Ответ: t =2 с; Т =4,31 Н; Е_к =1,32 Дж.

Задачи для самостоятельного решения

1. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинœетической энергии сплошного цилиндра.

2. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.

3. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определить кинœетическую энергию через 4 с после начала действия силы.

4. Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определить: а) момент сил торможения; б) момент инœерции вентилятора.

5. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н·м. Определить массу диска, в случае если известно, что его угловое ускорение постоянно и равно 16 рад/с².

6. С наклонной плоскости, составляющей угол 30⁰ с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, в случае если известно, что его центр масс при скатывании понизился на 30 см.

7. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кᴦ. Груз, разматывая нить, опускается с ускорением 2 м/с². Определить: а) момент инœерции вала; б) массу вала.

8. Горизонтальная платформа массой 25 кг и радиусом 0,8 м вращается с частотой 18 об/мин. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, в случае если человек, опустив руки, уменьшит свой момент инœерции от 3,5 кг·м² до 1 кг·м².

9. Человек массой 60 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся по инœерции вокруг неподвижной вертикальной оси с частотой 10 об/мин, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить, с какой частотой будет тогда вращаться платформа.

10. Платформа, имеющая форму сплошного однородного диска, может вращаться по инœерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, в случае если человек перейдет ближе к центру на расстояние, равное половинœе радиуса платформы.