Трехфакторный дисперсионный анализ

(латинский квадрат)

Дальнейшее уменьшение ошибки эксперимента можно получить введением еще одного исследуемого фактора, который выделит из общей дисперсии свою часть. При этом налагается еще одно ограничение на рандомизацию, что приводит к специальным планам эксперимента, называемым латинскими квадратами. Суть этого плана сводится к тому, что все три исследуемые фактора разбиваются на одинаковое число уровней n (как правило, n ≥4), при этом уровни 1-го фактора располагаются по столбцам плана, уровни 2-го – по строкам, а уровни 3-го, обозначенные в виде латинских букв, – в поле плана, причем их комбинация должна быть такой, чтобы каждая буква встречалась в каждом столбце и в каждой строке только один раз (таблица 4.3). Построение плана эксперимента по типу латинского квадрата позволяет осуществить экономный перебор вариантов испытаний.

Таблица 4.3 – План эксперимента типа латинский квадрат

Уровни 1-го фактора	Уровни 2-го фактора

	a	b	c	d
	b	c	d	a
	c	d	a	b
	d	a	b	c

По результатам испытаний вычисляется оценка дисперсий (таблица 4.4), которые позволяют построить дисперсионные отношения

F_{расч А}= / ; F_{расч В}= / ; F_{расч С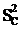}= / (4.2)

Сравнение найденных дисперсионных отношений с табличными значениями и выводы о верности или неверности гипотез об отсутствии эффектов соответствующих факторов производятся как в предыдущих случаях.

Символические значения в таблице 4.4 означают:

суммы наблюдений по 1-му фактору (по строкам)

суммы наблюдений по 2-му фактору (по столбцам)

суммы наблюдений по 3-му фактору (по буквам)

(например, суммируются все наблюдения, соответствующие букве a затем b и т.д.);

общая сумма

Латинские квадраты применяются предпочтительно для оценки линейных эффектов изучаемых факторов на начальных этапах исследования.

Таблица 4.4 – Формулы для расчета оценок дисперсий

Источник рассеяния	Число степеней свободы	Сумма квадратов	Дисперсия

Между уровнями 1-го фактора (между строками)	n -1
Между уровнями 2-го фактора (между столбцами)	n -1
Между уровнями 3-го фактора (между латинскими буквами)	n -1