Метод крутого восхождения (метод Бокса-Уилсона)

Метод крутого восхождения предложен Дж. Боксом и К. Уилсоном как синтез лучших черт градиентных методов и метода Гаусса-Зайделя, причем пробные опыты для выяснения направления движения выполняют методом полного факторного эксперимента (ПФЭ) или дробного факторного эксперимента (ДФЭ). От градиентных методов здесь воспринято выполнение рабочего движения вдоль вектор-градиента, определенного в районе исходной (базовой) точки, а от метода Гаусса-Зайделя взят принцип продвижения не на один рабочий шаг (как в методе градиента), а до достижения частного экстремума функции отклика на направлении градиента, без его корректировки на каждом рабочем шаге. Проведение ПФЭ или ДФЭ позволяет более точно оценивать направление градиента, чем при традиционном методе градиента, и получать информацию о взаимодействиях факторов и достаточно просто осуществлять статистическую проверку результатов расчетов.

На первом цикле метода крутого восхождения используется следующая процедура:

1 – Выбирают основную (базовую, нулевую) точку К₀ (рисунок 10.4). Правила ее выбора прежние.

2 – Выбирают интервал варьирования Δx_i для каждого фактора x_i (i = 1, 2, …, k) по изложенным ранее правилам.

3 – Определяют координаты пробных точек для нижнего и верхнего уровней варьирования факторов x_i по правилам ПФЭ

x_i_н = x_i₀ – Δx_i, x_i_в = x_i₀ + Δx_i (10.12)

и составляют ортогональную матрицу планирования ПФЭ или ДФЭ, для чего факторы нормируют по формуле:

x_i_б = (x_i – x_i₀) / Δx_i (10.13)

Затем выбирают число n серий параллельных опытов, порядок проведения опытов в сериях рандомизируют с помощью таблицы случайных чисел (Приложение А) и в этом порядке выполняют наблюдения отклика в точках ПФЭ и ДФЭ (на рисунке 10.4 это точки K₁, K₂, K₃, K₄).

x ₂

B A

K₁₁ K₁₀ K₉ K₈ K₇ K₆ K₅

x₂_В K₃ K₄

x₂₀K₀

x₂_Н K₁ K₂

x ₁

x_1Н x₁₀ x_1В

Рисунок 10.4 – Поиск экстремума функции отклика методом крутого восхождения

4 – По результатам ПФЭ (или ДФЭ) вычисляют оценки коэффициентов нормированного уравнения регрессии первого порядка

(10.15)

а также производят статистическую проверку значимости 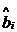, для чего можно рассчитать критическое значение коэффициентов:

= t_крs{ 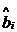}, (10.16)

где t_кр= t_табл {ν_зн; q}, выбираемое из таблицы (Приложение А) при числе степеней свободы ν_зн= N(n-1) и принятом уровне значимости β.

5 – Вычисляют расчетные i-е составляющие рабочих шагов в реальном масштабе:

λ_i = 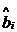Δx_i. (10.17)

Максимальное по модулю из всех λ_i (i=1, 2, …, k) принимают за базовое λ_баз.

6 – Получают практические (округленные) i-е составляющие рабочих шагов для продвижения вдоль направления градиента (на рисунке 10.4 это луч К₀А), для чего округляют (или изменяют) λ_баз до удобного λ_{баз.окр} и пропорционально этому округляют (или изменяют) остальные λ_i до λ_i_окр (i=1, 2, …, k). Округление λ_i производят по формуле

λ_i_окр = (λ_{баз.окр} / λ_баз) λ_i (10.18)

до удобного значения либо с учетом погрешностей измерения по каждому фактору x_i. Знаки λ_i_окр должны соответствовать (в случае поиска максимума, если отыскивается минимум, то знаки λ_i_окр должны быть противоположны) знакам оценок 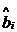коэффициентов.

7 – Вычисляют координаты m -х рабочих точек (m = 1, 2, …) на направлении градиента (на рисунке 10.4 это точки К₅– К₁₁) в реальном масштабе:

x_im = x_i₀ + m λ_i_окр; (10.19)

в них последовательно выполняют мысленные и проверочные (реальные) опыты. Размер λ_i обычно выбирают так, чтобы первая рабочая точка (m=1) не выходила за границы области ПФЭ или ДФЭ.

Мысленные опыты заключаются в получении предсказанных (расчетных) значений отклика по полученному линейному уравнению (10.15). Они позволяют:

– сокращать объем реальных опытов, то есть увеличить скорость продвижения к экстремуму;

– иметь представление, насколько хорошо уравнение (10.15) аппроксимирует реальную поверхность отклика, то есть насколько расчетные значения отличаются от результатов наблюдавшихся значений в реальных опытах;

– оценивать правильность выбора размера составляющих практического рабочего шага (λ_i_окр): если за число шагов k=3 достигается и превышается максимально возможное расчетное значение целевой функции (определяемое из физических свойств и ограничений, существующих для объекта), то λ_i_окрнужно уменьшить; если же число k слишком большое, то λ_i_окр следует увеличить или реже ставить реальные опыты.

Реальные (проверочные) опыты в начале движения из базовой точки вдоль направления градиента ставят через 2 – 4 мысленных опыта, а при уменьшении приращений наблюдавшихся значений отклика в каждом последующем реализованном по сравнению с предыдущим в рабочих точках проверочные ставят чаще, вблизи частного экстремума выполняют на каждом шаге.

Рабочее движение продолжают, пока не будет достигнут частный экстремум на направлении градиента (на рисунке 10.4 это точка К₉). Признаком достижения частного экстремума является уменьшение (в случае поиска максимума) отклика в последующих проверочных опытах.

8 – Точку частого экстремума на первоначальном направлении градиента (на рисунке 10.4 это точка К₉ на луче К₀А) принимают за новую нулевую точку и организуют второй цикл крутого восхождения. Порядок работы на втором цикле тот же, что и на первом. Различие состоит в том, что интервалы варьирования при постановке пробных опытов (ПФЭ или ДФЭ) и размер рабочих шагов в связи с приближением к экстремуму и увеличением кривизны поверхности отклика обычно выбирают меньшими, чем на первом цикле. В случае необходимости выполняют третий цикл крутого восхождения.

9 – Поисковое рабочее движение прекращают по достижении области экстремума. Признаком достижения экстремума является статистическая незначимость оценок 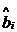коэффициентов при членах первого порядка, вычисленных по результатам ПФЭ (ДФЭ) вокруг очередной нулевой точки.

Достоинства метода крутого восхождения:

– высокая помехозащищенность (помехоустойчивость) в смысле точности оценивания составляющих градиента: если в градиентных методах каждая составляющая 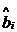оценивается лишь по двум точкам факторного пространства, то в ПФЭ, который в методе крутого восхождения используется для этой цели, каждый коэффициент 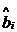оценивается по всем N=2^k точкам;

– высокая эффективность в смысле скорости движения к экстремуму; по сравнению с методом Гаусса-Зайделя она выше за счет продвижения по градиенту, а по сравнению с градиентным – за счет исключения пробных опытов на каждом рабочем шаге и за счет мысленных опытов;

– пробные опыты, выполняемые методом ПФЭ, позволяют получать информацию об оценках 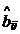коэффициентов при взаимодействиях факторов x_ix_j, характеризующих кривизну поверхности отклика: увеличение 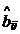при уменьшении 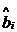обычно характеризует приближение к экстремуму;

– ПФЭ с применением параллельных опытов позволяет достаточно просто осуществлять надежную статистическую интерпретацию результатов;

– метод наиболее эффективен из известных при пологих поверхностях отклика.

Недостатком рассмотренного метода является несколько большая, чем в предыдущих методах, сложность планирования пробных опытов, требующая одновременного варьирования сразу всех факторов относительно базовой точки, и меньшая оперативность по сравнению с симплексным методом в условиях дрейфующих объектов.

Симплексный метод

Симплексом называют выпуклую фигуру (или тело), образованную k+1 вершинами в пространстве k факторов, причем эти k+1 вершин не принадлежат одновременно ни одному из подпространств из k-1 факторов. Симплекс называется регулярным, если все расстояния между его вершинами равны. В пространстве одного фактора (k=1) симплексом служит отрезок установленного размера, при k=2 – треугольник, при k=3 – тетраэдр. При k³4 привычным образом интерпретировать симплекс невозможно.

Симплексный метод позволяет совмещать пробные опыты для определения направления движения с рабочим движением по поверхности отклика к области оптимума. Основная идея симплексного метода в следующем. Если во всех k+1 вершинах симплекса поставить опыты и измерить отклик, то (при не слишком большом уровне шумов) по величине отклика в вершинах можно судить, в каком направлении следует двигаться, чтобы приблизиться к экстремуму. После проведения серии опытов, поставленных в вершинах правильного симплекса, определяется точка, соответствующая условиям, при которых получаются наихудшие результаты. Затем используется важное свойство симплекса, по которому из любого симплекса можно, отбросив одну из вершин, получить новый, заменив отброшенную вершину ее зеркальным отражением относительно противоположной его грани. Если отбросить точку с наихудшими результатами и построить на оставшейся грани новый симплекс, то его центр будет смещен в направлении: худшая точка – центр тяжести остальных точек, то есть в направлении к экстремуму. Затем процесс отбрасывания вершины с наихудшим значением целевой функции и построения нового симплекса повторяется. Если значение выхода в новой вершине снова окажется наихудшим, то нужно вернуться к исходному симплексу и отбросить следующую по порядку вершину с плохим результатом. В результате этого образуется цепочка симплексов, перемещающихся в факторном пространстве к точке экстремума. Таким образом, движение к экстремуму осуществляется путем зеркального отражения точки с наихудшими результатами относительно центра противоположной грани симплекса.

Порядок работы при использовании симплексного метода следующий:

1 – Выбирают начальную точку С₁, а также интервалы варьирования Δx_i для всех факторов (i=1, 2, …, k).

2 – Выбирают безразмерную величину r_сим стороны (или ребра) симплекса в относительных единицах по отношению к интервалам варьирования Δx_i. Наиболее просто выбрать r_сим=1. Стремятся, чтобы в безразмерных единицах стороны симплекса были равны.

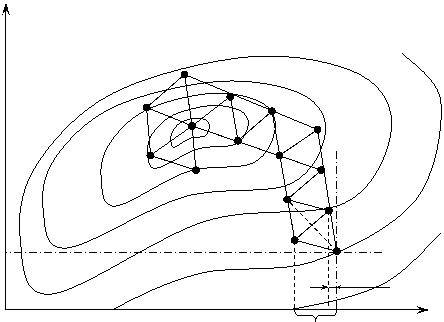
3 – Вычисляют координаты остальных вершин начального симплекса. Обычно для этого используют следующее правило. Через начальную точку С₁ проводят осевые линии, параллельные координатным осям, и выбирают квадрант, в котором по предположению, должен располагаться экстремум целевой функции. В начальную точку помещают вершину симплекса С₁ (рисунок 10.5), а сам симплекс I располагают так, чтобы его стороны образовали с осевыми линиями равные углы.

При таком расположении начального симплекса координаты его вершин определяют с помощью матрицы (таблица 10.1), в которой даны координаты вершин (k+1)-мерного симплекса в n-факторном пространстве.

x ₂

C₁₂

C₁₀

C₁₃ C₈

C₁₁ C₇

C₁₄ C₉ C₆

C₅

C₄

C₃

C₂

x₂₀ C₁

qΔx₁

x₁₀ x ₁

pΔx₁

Рисунок 10.5 – Поиск экстремума функции отклика симплексным методом

Безразмерные относительные величины p и q при таком расположении симплекса определяют по формуле:

(10.20)

На рисунке 10.5 показаны размеры pΔx₁ и qΔx₁ для случая r_сим=1. Если принимают r_сим¹1, то Δx_i умножают еще на r_сим. Знаки Δx_i зависят от номера квадранта, в котором расположен начальный симплекс. Для k=2 имеем p≈0,966, q≈0,259.

Таблица 10.1 –Задание координат вершин симплекса

Факторы x_i	x₁	x₂	x₃	…	x_i	…	x_k
Вершина C₁	x₁₀	x₂₀	x₃₀	…	x_i₀	…	x_k₀
Вершина C₂	x₁₀+pΔx₁	x₂₀+qΔx₂	x₃₀+qΔx₃	…	x_i0+qΔx_i	…	x_k₀+qΔx_k
Вершина C₃	x₁₀+qΔx₁	x₂₀+pΔx₂	x₃₀+qΔx₃	…	x_i0+qΔx_i	…	x_k₀+qΔx_k
…	…	…	…	…	…	…	…
Вершина C_i₊₁	x₁₀+qΔx₁	x₂₀+qΔx₂	x₃₀+qΔx₃	…	x_i0+pΔx_i	…	x_k₀+qΔx_k
…	…	…	…	…	…	…	…
Вершина C_k₊₁	x₁₀+qΔx₁	x₂₀+qΔx₂	x₃₀+qΔx₃	…	x_i0+qΔx_i	…	x_k₀+pΔx_k

4 – В вершинах симплекса выполняют наблюдения отклика и сравнивают по величине; выбирают вершину с минимальным откликом и отражают ее относительно противолежащей стороны или грани; находят вершину следующего симплекса II, n вершин которого одновременно являются и вершинами предыдущего симплекса I. Координаты отраженной вершины вычисляют по формуле

(10.21)

где i – номер фактора (i=1, 2, …, k);

l – номер вершины m-го симплекса, где обнаружен минимальный (в случае нахождения максимума) отклик;

m+1 – номер последующего симплекса, содержащего отраженную вершину (ей условно присваивают тот же номер l);

k – число факторов.

Если минимальный отклик оказался сразу в двух вершинах, то вопрос, какую из них отражать, решают произвольно.

5 – Ставят эксперимент в отраженной вершине нового симплекса и отклик в ней сравнивают с откликами в остальных вершинах, а затем снова выбирают вершину с минимальным откликом и отражают ее через противолежащую сторону (или грань) симплекса. Если в новой вершине (m+1)-го симплекса отклик оказался опять минимальным, то возвращаются к m-му симплексу и отражают вторую по минимальности вершину. Если это явление повторяется, то отражают третью по минимальности вершину и так далее.

6 – Эксперимент продолжают до тех пор, пока симплекс не совершит полный оборот вокруг одной из вершин. На рисунке 10.5 это вершина С₁₁.

Точность нахождения точки экстремума зависит от двух причин: размера симплекса и влияния помех. Для уточнения положения экстремальной точки статического объекта в последних симплексах рекомендуется ставить параллельные опыты, чтобы снизить влияние помех, а также выполнить опыт в середине того симплекса, в вершинах которого отклик оказался максимальным по сравнению с остальными симплексами.

Достоинства симплексного метода:

– достаточно высокая помехоустойчивость в смысле выбора направления движения к экстремуму;

– изучение поверхности отклика сочетается с одновременным рабочим движением к экстремуму;

– при оптимально выбранном размере симплекса обеспечивается высокая скорость выхода к области экстремума;

– высокая оперативность, позволяющая использовать этот метод особенно для непрерывной оптимизации объектов с дрейфующим экстремумом.

Недостатки метода:

– метод не позволяет непосредственно получать математическое описание изучаемого участка поверхности отклика, как, например, в методе Бокса-Уилсона;

– в условиях пологих поверхностей отклика симплексный метод дает менее точное решение, чем метод крутого восхождения.

10.7Решение типового примера

Пример Оптимизация процесса проводится в соответствии с априорной информацией по трем факторам: температура испарения (А), температура подложки при осаждении (В) и термообработки (С) резистивных пленок рения. Значения переменных при исследовании свойств резистивных пленок приведены в таблице 10.2.

Таблица 10.2 – Значения переменных при исследовании резистивных пленок

Фактор	А	В	С
Кодовые обозначения	X₁	X₂	X₃
Основной уровень X_i₀	2500⁰С	400⁰С	400⁰С
Интервал варьирования ΔX_i	50⁰С	50⁰С	50⁰С

Решение В результате исследования получено математическое описание исследуемой области (процесс получения модели представлен в практическом занятии №6)

Y_t=2,15 – 0,1X_1б– 0,1X_2б– 0,2X_3б,

где Y_t – теоретическое значение функции отклика (параметр оптимизации), в качестве которого выбран температурный коэффициент сопротивления резистивных пленок (ТКС·10⁴/⁰C);

X_i_б – приведенные переменные (безразмерные значения факторов), полученные по (10.13).

Последовательность процесса оптимизации представлена в таблице 10.3.

Таблица 10.3 – План проведения и результаты эксперимента, проведенного методом крутого восхождения

Факторы	X₁	X₂	X₃	Значения функции отклика
Коэффициент b_i	-0,1	-0,1	-0,2
b_iΔX_i	-5,0	-5,0	-10,0
Шаг варьирования	5,0⁰С	5,0⁰С	10,0⁰С
Исходная (начальная) точка	2550⁰С	450⁰С	450⁰С	Y_ξt	Y_ξ
Первый реализованный опыт Второй реализованный опыт Третий реализованный опыт Четвертый реализованный опыт Пятый реализованный опыт	2570⁰С 2590⁰С 2610⁰С 2630⁰С 2650⁰С	470⁰С 490⁰С 510⁰С 530⁰С 550⁰С	490⁰С 530⁰С 570⁰С 610⁰С 650⁰С	1,50 1,25 1,00 0,80 0,55	1,70 1,40 1,30 1,00 1,10

По программе «крутого восхождения» (таблица 10.3) намечены так называемые «мысленные опыты» и некоторые их них (через три) реализованы для проверки соответствия теоретического значения, предсказанного для j- го опыта (Y_ξt) полученным в результате ПФЭ уравнением, и соответствующего экспериментального значения (Y_ξ). Пятый опыт не показал уменьшения ТКС по сравнению с четвертым реализованным, и экспериментальное значение ТКС Y_ξ=1,1 существенно отличается от его теоретического значения Y_ξt=0,55. Поэтому продолжать движение в прежнем направлении не имеет смысла. Целесообразно поставить новую серию опытов с центром в точке 4 (как имеющей наилучший результат) и найти новое направление для движения к экстремуму.

Задачи для решения

1. Оптимизировать математические модели в виде полиномов 1-порядка, полученные в результате обработки результатов активного эксперимента (практические занятия № 6, 7, 8).

2. Найти минимум функции:

2.1

2.2

2.3

2.4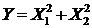

2.5

2.6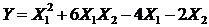

2.7

2.8

2.9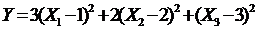

2.10

Контрольные вопросы

1. Как формулируется задача оптимизации?

2. Какими подходами можно решить задачу оптимизации?

3. Что общего у всех методов экспериментального поиска экстремума?

4. В чем заключается основная идея и процедура метода Гаусса-Зайделя?

5. В чем заключается основная идея и процедура метода случайного поиска?

6. В чем заключается основная идея и процедура обычного градиентного метода?

7. В чем заключается основная идея и процедура метода Кифера-Вольфовица?

8. В чем заключается основная идея и процедура симплексного метода?

9. В чем заключается основная идея и процедура метода крутого восхождения (Бокса-Уилсона)?

10. Сравните известные поисковые методы по помехоустойчивости в смысле выбора направления движения.

11. Сравните поисковые методы по помехоустойчивости в смысле точности выхода к экстремуму.

12. Сравните методы поиска по эффективности, то есть по скорости выхода к экстремуму.

13. Каковы достоинства и недостатки поисковых методов?

14. Что служит критерием достижения экстремума в поисковых методах?

15. В чем состоит роль мысленных опытов и как они проводятся?

16. Как выполняется статистический анализ результатов в методе крутого восхождения?

17. Как выполняется оптимизация при многоэкстремальной поверхности отклика?

18. Что служит критерием для выбора начальной точки исследования?

19. Что служит критерием для выбора интервала варьирования для каждого фактора?

Литература

1. Воронина О.А. Математические основы планирования и проведения эксперимента. Учеб. пособие / О.А. Воронина - Орел: ОрелГТУ – 2007.

2. Современный эксперимент: подготовка, проведение, анализ результатов / В.Г. Блохин, О.П. Глудкин, А.И. Гуров, М.А Ханин. Под ред. О.П. Глудкина – М.: Радио и связь, 1997.

3. Статистические методы в инженерных исследованиях (лабораторный практикум): Учеб. пособие / В.П. Бородюк, А.П. Вощинин, А.З. Иванов и др. Под ред. Г.К. Круга – М.: Высшая школа, 1983.

4. Грачев Ю.П. Математические методы планирования эксперимента / Ю.П. Грачев, Ю.М. Плаксин Ю.М - М.: ДеЛи принт 2005 г.

5. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников / А.И. Кобзарь - М.: ФИЗМАТЛИТ, 2006

6. Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL: учебное пособие / Э. А. Вуколов — М.: ФОРУМ: ИНФРА-М, 2010

7. Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. / В.В. Денисенко - М.: Горячая линия-Телеком, 2009.

8. ГОСТ Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения

9. Охорзин В.А. Прикладная математика в системе MATHCAD: Учебное пособие. / В.А. Охорзин – СПб.: Лань, 2008.

10. Лагутин М. Б. Наглядная математическая статистика / М. Б. Лагутин - М.: Бином. Лаборатория знаний, 2007.

11. Макаров А.А. Анализ данных на компьютере / Ю.Н Тюрин, А.А. Макаров – М.: Инфра-М, 2003.

12. Львович Я.Е. Теоретические основы конструирования, технологии и надежности РЭА: Учеб. пособие для вузов / Я.Е.Львович, В.Н.Фролов - М.: Радио и связь, 1986.

13. Журнал «Математическое моделирование» [Электронный ресурс] http://www.mathnet.ru/php/journal.phtml?jrnid=mm&option_lang=rus

Приложение А

(обязательное)

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: