Примеры сетевых стуктур

Модель Кохонена (T.Kohonen, 1982) обобщает предъявляемую информацию. В результате работы НС Кохонена создается образ, представляющий собой карту распределения векторов из обучающей выборки.

Таким образов, в модели Кохонена выполняется решение задачи нахождения кластеров в пространстве входных образов. Такая сеть обучается без учителя на основе самоорганизации. По мере обучения векторы весов нейронов стремятся к центрам кластеров - групп векторов обучающей выборки. На этапе решения информационных задач сеть относит новый предъявленный образ к одному из сформированных кластеров, указывая тем самым категорию, к которой он принадлежит.

Сеть Кохонена состоит из одного слоя нейронов. Число входов каждого нейрона равно размерности входного образа. Количество же нейронов определяется той степенью подробности, с которой требуется выполнить кластеризацию набора библиотечных образов. При достаточном количестве нейронов и удачных параметрах обучения НС Кохонена может не только выделить основные группы образов, но и установить "тонкую структуру" полученных кластеров. При этом близким входным образам будет соответствовать близкие карты нейронной активности.

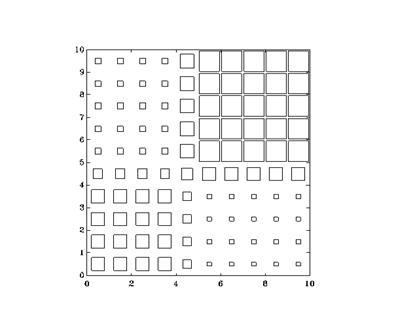Рис. Пример карты Кохонена. Размер каждого квадратика

соответствует степени возбуждения соответствующего нейрона.

 

Обучение начинается с задания случайных значений матрице связей W_n^m. В дальнейшем происходит процесс самоорганизации, состоящий в модификации весов при предъявлении на вход векторов обучающей выборки. Для каждого нейрона можно определить его расстояние до вектора входа:

.

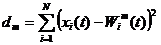Далее выбирается нейрон m = m ^*, для которого это расстояние минимально. На текущем шаге обучения t будут модифицироваться только веса нейронов из окрестности нейрона m *:

.

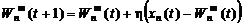Первоначально в окрестности любого из нейронов находятся все нейроны сети, впоследствии эта окрестность сужается. В конце этапа обучения подстраиваются только веса самого ближайшего нейрона. Темп обучения h(t) < 1 с течением времени также уменьшается. Образы обучающей выборки предъявляются последовательно, и каждый раз происходит подстройка весов. Нейронная сеть Кохонена может обучаться и на искаженных версиях входных векторов, в процессе обучения искажения, если они не носят систематического характера, сглаживаются.

Для наглядности представления карты нейроны Кохонена могут быть упорядочены в двумерную матрицу, при этом под окрестностью нейрона-победителя понимаются соседние (по строкам и столбцам) элементы матрицы. Результирующую карту удобно представить в виде двумерного изображения, на котором различные степени возбуждения всех нейронов отображаются квадратами различной площади. Пример карты, построенной по 100 нейронам Кохонена, представлен на рис.

Каждый нейрон несет информацию о кластере - сгустке в пространстве входных образов, формируя для данной группы собирательный образ. Таким образом, НС Кохонена способна к обобщению. Конкретному кластеру могут соответствовать и несколько нейронов с близкими значениями векторов весов, поэтому выход из строя одного нейрона не так критичен для функционирования НС Кохонена.

 

Вопрос 5. Методы и алгоритмы ОРО - кластерный анализ, генетический алгоритм.

 

Кластерный анализ.

Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации (cluster (англ.) - гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:

а) внутри групп объекты должны быть тесно связаны между собой;

б) объекты разных групп должны быть далеки друг от друга;

в) при прочих равных условиях распределения объектов по группам должны быть равномерными.

Требования а) и б) выражают стандартную концепцию компактности классов разбиения; требование в) состоит в том, чтобы критерий не навязывал объединения отдельных групп объектов.

Узловым моментом в кластерном анализе считается выбор метрики (или меры близости объектов), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т.п. При применении экстенсиональных методов распознавания, как было показано в предыдущих разделах, выбор метрики достигается с помощью специальных алгоритмов преобразования исходного пространства признаков.

Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов. Пусть w_i - i- я группа (класс, кластер) объектов, N_i - число объектов, образующих группу w_i, вектор m_i - среднее арифметическое объектов, входящих в w_i (другими словами m_i - "центр тяжести" i -й группы), a q (w_l, w_m) - расстояние между группами w_l и w_m.

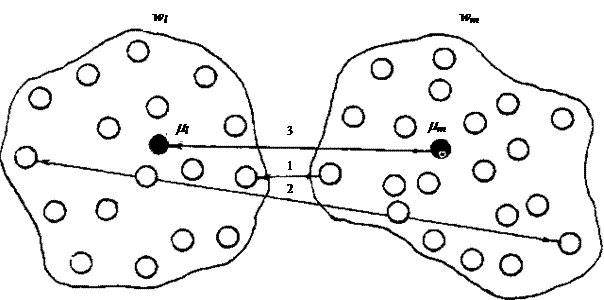
Рис. Различные способы определения расстояния между кластерами w_l и w_m: 1 - по ближайшим объектам, 2 - по самым далеким объектам, 3 - по центрам тяжести.

Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:

.

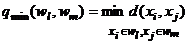Расстояние дальнего соседа - расстояние между самыми дальними объектами кластеров:

.

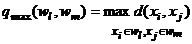Расстояние центров тяжести равно расстоянию между центральными точками кластеров:

.

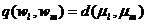Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную, структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. Промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.

Нацеленность алгоритмов кластерного анализа на определенную структуру группировок объектов в пространстве признаков может приводить к неоптимальным или даже неправильным результатам, если гипотеза о типе группировок неверна. В случае отличия реальных распределений от гипотетических указанные алгоритмы часто "навязывают" данным не присущую им структуру и дезориентируют исследователя. Поэтому экспериментатор, учитывающий данный факт, в условиях априорной неопределенности прибегает к применению батареи алгоритмов кластерного анализа и отдает предпочтение какому-либо выводу на основании комплексной оценки совокупности результатов работы этих алгоритмов.

Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. В то же время большинство таких алгоритмов состоит из двух этапов. На первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации. Затем, на втором этапе, объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.

Многообразие алгоритмов кластерного анализа обусловлено также множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Простейший критерий качества непосредственно базируется на величине расстояния между кластерами. Однако такой критерий не учитывает "населенность" кластеров - относительную плотность распределения объектов внутри выделяемых группировок. Поэтому другие критерии основываются на вычислении средних расстояний между объектами внутри кластеров. Но наиболее часто применяются критерии в виде отношений показателей "населенности" кластеров к расстоянию между ними. Это, например, может быть отношение суммы межклассовых расстояний к сумме внутриклассовых (между объектами) расстояний или отношение общей дисперсии данных к сумме внутриклассовых дисперсий и дисперсии центров кластеров.

Разнообразные процедуры кластерного анализа входят в состав практически всех современных пакетов прикладных программ для статистической обработки многомерных данных.

 

Генетический алгоритм

Генетический алгоритм (ГА) является самым известным на данный момент представителем эволюционных алгоритмов, и, по своей сути, алгоритмом для нахождения глобального экстремума многоэкстремальной функции. ГА моделирует размножение живых организмов.

Для начала представим себе целевую функцию от многих переменных, у которой необходимо найти глобальный максимум или минимум:

f (x ₁, x ₂, x ₃, …, x_N). (5.31)

Для того чтобы заработал ГА, необходимо представить независимые переменные в виде хромосом. Первым шагом является преобразование независимых переменных в хромосомы, которые будут содержать всю необходимую информацию о каждой создаваемой особи. Имеется два варианта кодирования параметров:

в двоичном формате;

в формате с плавающей запятой.

Если сравнивать эти два способа представления, то более хорошие результаты дает вариант представления в двоичном формате.

Генетический алгоритм работает следующим образом. В первом поколении все хромосомы генерируются случайно. Определяется их "полезность". Начиная с этой точки, ГА может начинать генерировать новую популяцию. Обычно, размер популяции постоянен. Репродукция состоит из четырех шагов:

селекции и трех генетических операторов (порядок применения не важен);

кроссовера;

мутации;

инверсии.

Кроссовер является наиболее важным генетическим оператором. Он генерирует новую хромосому, объединяя генетический материал двух родительских. Существует несколько вариантов кроссовера. Наиболее простой - одноточечный, где берутся две хромосомы и перерезаются в случайно выбранной точке. Результирующая хромосома получается из начала одной и конца другой родительских хромосом:

001100101110010|11000	®	001100101110010 11100
110101101101000|11100

 

Мутация представляет собой случайное изменение хромосомы (обычно простым изменением состояния одного из битов на противоположное). Данный оператор позволяет ГА более быстро находить локальные экстремумы, с одной стороны, и "перескочить" на другой локальный экстремум - с другой:

00110010111001011000

®

00110010111001111000

 

Инверсия инвертирует (изменяет) порядок битов в хромосоме путем циклической перестановки (случайное количество раз). Многие модификации ГА обходятся без данного генетического оператора.

00110010111001011000

®

11000001100101110010

 

Очень важно понять, за счет чего ГА на несколько порядков превосходит по быстроте случайный поиск во многих задачах. Дело, видимо, в том, что большинство систем имеют довольно независимые подсистемы. Вследствие этого, при обмене генетическим материалом часто может встретиться ситуация, когда от каждого из родителей берутся гены, соответствующие наиболее удачному варианту определенной подсистемы (остальные "уродцы" постепенно вымирают). Другими словами, ГА позволяет накапливать удачные решения для систем, состоящих из относительно независимых подсистем (а это большинство современных сложных технических систем и все известные живые организмы). Соответственно, можно предсказать, когда ГА скорее всего даст сбой (или, по крайней мере, не покажет особых преимуществ перед методом Монте-Карло) - системы, которые сложно разбить на подсистемы (узлы, модули), а также при неудачном порядке расположения генов (рядом расположены параметры, относящиеся к различным подсистемам), когда преимущества обмена генетическим материалом сводятся к нулю. Последнее замечание несколько ослабляется в системах с диплоидным (двойным) генетическим набором.