Список вопросов для защиты лабораторной работы

Лабораторная работа 3.

Подбор полиномиальной зависимости методом наименьших квадратов. Решение СЛАУ.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Задана система точек (узлы интерполяции) x_i, i = 1,2,...,N; a £ x_i £ b, и значения f_i, i = 1,2,....,N. Требуется построить многочлен 3-ей степени P₃(x)=a₁+a₂x+a₃x²+a₄x³, имеющий в узлах интерполяции минимальное отклонение от заданных значений f_i. В i -ой точке полином P₃(x) отклоняется от значения f_i на величину (P₃(x_i)-f_i). Суммируя квадраты отклонений полинома по всем точкам i=1,2,…N, построим функционал

.

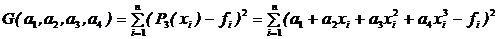Найдем min 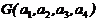. Для этого приравняем нулю все частные производные 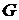. Собирая коэффициенты при неизвестных a_i, получим нормальную систему ‑ СЛАУ относительно вектора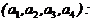

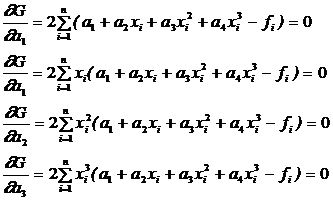
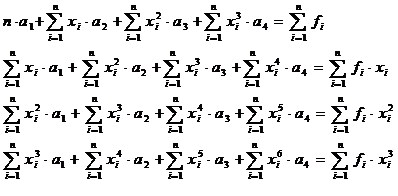
В матричном виде систему можно записать: B a = C. (1)

B – матрица системы, a – искомый вектор, с – вектор правой части. Решение СЛАУ найдем с помощью точного метода Гаусса, а также с помощью итерационного метода релаксации.

МЕТОД РЕЛАКСАЦИИ

ШАГ 1. Запишем систему (1) в виде a = a ‑ t (B a – c), t > 0 ‑ параметр, значение которого подбирается таким образом, чтобы построенный итерационный метод сходился.

ШАГ 2. Зададим точность метода e >0, параметр релаксации t > 0, введем вектор начального приближения к решению a0. Вектор может быть произвольным, например, нулевым:. a0 = (0, 0,..., 0).

ШАГ 3. Следующее приближение ‑ вектор a1 находится следующим образом: a1 = a0 ‑ t (B a0 – c), или, в скалярном виде: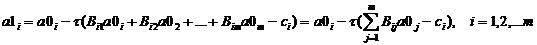

ШАГ 4. Вычислим вектор невязки: r = a1 – a0 и его норму: ║ r ║ = max (r _i)..

ШАГ 5. Приготовимся к следующей итерации. Занесем компоненты вектора a1 в вектор a0, т.е. a0_i:=a1_i. I=1,2..m.

ШАГИ 3-5 образуют итерационный цикл. Будем повторять их до тех пор, пока не выполнится условие ║ r ║ < e.

ВЫПОЛНЕНИЕ ЗАДАНИЯ

1. Открыть файл MNK.xls в папке своей группы, найти рабочий лист с номером своего варианта. Используя функцию суммирования Excel, вычислить коэффициенты матрицы B и вектора правых частей c.

2. Используя встроенные функции Excel (см рабочие листы Пример 3, Пример 4, Пример 5 в файле MNK.xls), решить СЛАУ методом обратной матрицы и методом Крамера. Выписать искомый полином, построить его график и нанести заданные точки.

3. Запустить тестовый вариант программы метода Гаусса (программа gauss_t.pas). Должны получиться следующие результаты: 2.2133, 0.0781, -3.6163, 2.4822.

4. Изменить исходные данные программы метода Гаусса (матрицу B и вектор с) и найти решение (коэффициенты полинома) для своего варианта. На печать вывести коэффициенты полинома и значение функционала отклонений G для найденных значений коэффициентов. Показать, что для любого другого вектора, произвольно введенного с клавиатуры, получится большее значение функционала отклонений G.

5. Написать программу решения системы (1) с помощью метода релаксации для e=10^-3. Для подбора значения параметра t, обеспечивающего сходимость итерационного процесса, на каждой итерации выводить на экран промежуточные результаты – вектор a1 и норму вектора невязки ║ r ║. В случае, если невязка растет, остановить выполнение программы (<ctrl>+<C>), заново запустить ее и задать меньшее значение t.

Результаты занести в Таблицу 1:

t	Сходимость процесса
	Не сходится
0.5	Не сходится
0.25	Не сходится
0.1	Сходится

6. После выбора значения t, обеспечивающего сходимость итерационного процесса, убрать промежуточную печать и добавить в программу счетчик количества итераций. Для e=10^-3 подобрать оптимальное значение параметра, т.е. такое значение, при котором метод сходится с наименьшим количеством итераций. Результаты занести в Таблицу 2:

t	Количество итераций для e=10-3
0.1
0.15
0.125

7. Для оптимального значения параметра t просчитать варианты с изменением точности e=10^-2, 10^-3, 10^-4. Сравнить полученные результаты a₁, a₂, a₃, a₄ с результатами, полученными по методу Гаусса. Результаты занести в Таблицу 3

e	Количество итераций	a1	a2	a3	a4
10-2
10-3
10-4
РЕШЕНИЕ по М. ГАУССА

3. В ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ 3 ВКЛЮЧИТЬ:

1. Постановку задачи (что задано, что надо найти).

2. Описание метода наименьших квадратов на примере подбора линейной зависимости g(x)=a₁+a₂x. Выписать точные формулы для нахождения a₁, a₂.

3. Описание МНК для задачи подбора полинома третьего порядка. Выписать матрицу 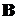и вектор правых частей С нормальной системы.

4. Описание метода Гаусса.

5. Результаты решения системы по методу Гаусса и искомый полином.

6. Значения функционала отклонений G при найденных значениях коэффициентов. Значения функционала отклонений G для других коэффициентов a₁, a₂, a₃, a₄, близких к найденным.

7. Описание метода простой итерации.

8. Текст программы метода релаксации.

9. Таблицы 1‑3 с пояснениями.

10. Выводы.

СПИСОК ВОПРОСОВ ДЛЯ ЗАЩИТЫ ЛАБОРАТОРНОЙ РАБОТЫ

1. Метод наименьших квадратов на примере подбора эмпирической зависимости F=a+bx+cx²+dx^3,, F=a+bx
и др.Как решить нормальную систему?

2. Записать СЛАУ в скалярном, векторном и матричном виде. Что известно, что надо найти? При каком условии существует единственное решение? Обусловленность матрицы. Точные и приближенные методы.

3. Метод обратной матрицы. Привести примеры других точных и приближенных методов решения СЛАУ.

4. Как выполняются действия над матрицами: сумма, произведение на константу, произведение матриц. Верно ли, что A*B=B*A, где A, B ‑ квадратные матрицы размерности NхN.

5. Расширенная матрица СЛАУ. Какие операции над СЛАУ не меняют ее решения? Какие действия над расширенной матрицей соответствуют эквивалентными преобразованиями СЛАУ?

6. Метод Крамера на примере решения системы трех уравнений с тремя неизвестными.

7. Метод Гаусса: прямой ход (сведение СЛАУ с системе с верхней треугольной матрицей).

8. Метод Гаусса: обратный ход (решение СЛАУ с верхней треугольной матрицей).

9. Вывести формулы для нахождения решения СЛАУ с нижней треугольной матрицей.

10. Понятие экономичности метода решения СЛАУ. Оценка количества операций методов Крамера и Гаусса. Почему точные методы не используют для решения больших СЛАУ?

11. Описать основные этапы итерационного метода решения СЛАУ.

12. Выбор начального приближение в итерационных методах решения СЛАУ. Критерии остановки итераций. Вектор невязки. Как можно оценить его величину?

13. Условие сходимости метода итераций для решения СЛАУ. Норма матрицы. Метод Якоби. Условие диагонального преобладания. Метод релаксации.