III Региональная студенческая олимпиада по элементарной математике 25.11.2017
В квадратном уравнении поменяли местами старший коэффициент и свободный член. У получившихся уравнений один корень оказался общим, два других различные. Докажите, что эти два других корня взаимно обратные.
2. Внутри квадрата ABCD построен равносторонний треугольник ABK. Прямые BK и AD пересекаются в точке P. Докажите, что отрезок, соединяющий середины отрезков KD и CP, равен половине стороны квадрата.
Даны несколько различных натуральных чисел. Произведение двух самых больших из них равно сумме всех чисел. Найдите эти числа.
4. Даны семь чисел. Разрешается взять любые два числа и заменить каждое на их среднее арифметическое. Докажите, что за несколько таких операций можно сделать равными шесть чисел.
На плоскости расположены несколько прямых, любые две из которых пересекаются. Через каждую точку пересечения проходят не менее трех прямых. Докажите, что все прямые пересекаются в одной точке.
Имеются шесть монет, одна из которых фальшивая, отличается по весу от настоящих одинакового веса. Вес настоящей и фальшивой монеты неизвестен. Как за три взвешивания на весах, показывающих общий вес взвешиваемых монет, найти фальшивую монету?
Решения задач
1. Пусть ax 2 + bx + c = 0 исходное уравнение, тогда второе уравнение имеет вид cx 2 + bx + a = 0. Пусть x 1 – общий корень этих уравнений. Тогда выполняются равенства ax 12 + bx 1 + c = 0, cx 12 + bx 1 + a = 0. Вычитаем из первого равенства второе, получаем x 12(a – с) +(c – а) = 0, x 12(a – с) = а – c. Так как у уравнений есть различные корни, то а ¹ c, откуда x 12 = 1, и x 1 = ±1. Вторые корни находим по теореме Виета: в первом уравнении это x 2¢ = ± c / a, во втором уравнении x 2¢¢ = ± a / c (знаки одинаковы).
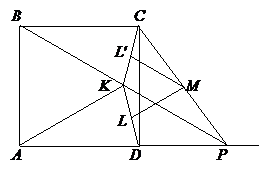 2. Заметим, что KM – средняя линия треугольника BCP, и прямая KM является осью симметрии квадрата. Относительно нее симметричны отрезки KD и CK, а значит и их середины, точки L и L ¢. Тогда LM = L ¢ M. А так как L ¢ M – средняя линия треугольника KCP, то L ¢ M =
2. Заметим, что KM – средняя линия треугольника BCP, и прямая KM является осью симметрии квадрата. Относительно нее симметричны отрезки KD и CK, а значит и их середины, точки L и L ¢. Тогда LM = L ¢ M. А так как L ¢ M – средняя линия треугольника KCP, то L ¢ M = 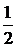 KP =
KP = 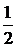 BK =
BK = 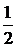 AB.
AB.
3. Возможный пример таких чисел – 1, 2, 3. Докажем, что других наборов не существует. Пусть в таком наборе a и b – самые большие числа, a < b. Тогда сумма всех чисел не превышает 1 + 2 + … + a + b = 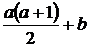 , откуда
, откуда 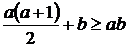 ,
, 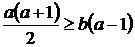 , и
, и 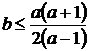 . А так как a < b, то
. А так как a < b, то 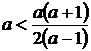 . Отсюда a < 3. Подходит только а = 2, при котором получаем указанный выше набор.
. Отсюда a < 3. Подходит только а = 2, при котором получаем указанный выше набор.
4. Если есть k равных чисел и k других равных между собой чисел, то легко получить 2 k равных чисел: по очереди берем по одному числу из каждой группы и заменяем на их среднее арифметическое. Таким методом делаем равными четыре числа. Одно из них добавляем к трем оставшимся и делаем эти четыре числа равными. Затем берем три равных числа из первой группы и три равных числа из второй группы, делаем из них шесть равных между собой.
 5. Предположим, что есть прямая a и точка вне её, в которой пересекаются другие прямые. Если таких точек несколько, то выберем из них точку A, ближайшую к прямой a. Через точку A проходят не менее трех прямых b, c, d. Они пересекаются с прямой a в точках B, C, D соответственно. Пусть точка С лежит между А и D. Через точку C проходит ещё одна прямая l. Она пересекает либо отрезок AB, либо отрезок AD в точке L, которая расположена к прямой а ближе, чем точка А. Это противоречит выбору точки A.
5. Предположим, что есть прямая a и точка вне её, в которой пересекаются другие прямые. Если таких точек несколько, то выберем из них точку A, ближайшую к прямой a. Через точку A проходят не менее трех прямых b, c, d. Они пересекаются с прямой a в точках B, C, D соответственно. Пусть точка С лежит между А и D. Через точку C проходит ещё одна прямая l. Она пересекает либо отрезок AB, либо отрезок AD в точке L, которая расположена к прямой а ближе, чем точка А. Это противоречит выбору точки A.
6. Пусть вес настоящей монеты равен а, фальшивой – b. Взвешиваем сначала первую и вторую монеты, затем третью и четвертую. Если вес окажется одинаковым, то все монеты настоящие, и мы узнаём вес настоящей монеты. Взвешиваем пятую монету, и если она оказывается настоящей, то фальшивая – шестая.
Если же первые два взвешивания дадут разный результат, то находим средний вес взвешенных монет. Один из них будет равен а, другой (a + b)/2. Пятая и шестая монеты настоящие. Взвешиваем первую, третью и пятую монеты. Если их средний вес совпадает с одним из полученных при первых двух взвешиваниях, то это вес настоящей монеты, и фальшивая – та которая осталась в паре с другим средним весом. Если же результат отличается от первых двух, то фальшивая монета в третьей партии, и средний вес окажется равным (2 a + b)/3. Сравним его с первыми двумя результатами:
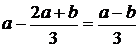 ;
; 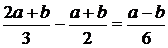 .
.
Видим, что этот результат ближе к результату с фальшивой монетой. Значит, фальшивая монета попала из пары, в которой средний вес оказался ближе к третьему результату.
 2017-12-14
2017-12-14 227
227







