(D -СХЕМЫ)
Рассмотрим особенности непрерывно-детерминированного подхода на примере использования в качестве математических моделей дифференциальных уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями.
Основные соотношения. Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем (2.6) в общем виде будет
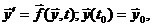 (2.7)
(2.7)
где 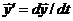 ,
, 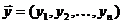 и
и 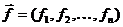 — n -мерные векторы;
— n -мерные векторы; 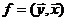 — вектор-функция, которая определена на некотором
— вектор-функция, которая определена на некотором 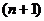 -мерном
-мерном 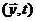 множестве и является непрерывной.
множестве и является непрерывной.
Так как математические схемы такого вида отражают динамику изучаемой системы, т. е. ее поведение во времени, то они называются D-схемами (англ. dynamic) [4, 37].
В простейшем случае обыкновенное дифференциальное уравнение имеет вид
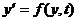 (2.8)
(2.8)
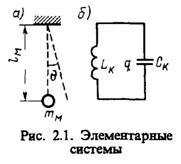
Наиболее важно для системотехники приложение D-схем в качестве математического аппарата в теории автоматического управления. Для иллюстрации особенностей построения и применения D-схем рассмотрим простейший пример формализации процесса функционирования двух элементарных систем различной физической природы: механической  (колебания маятника, рис. 2.1, а) и электрической
(колебания маятника, рис. 2.1, а) и электрической  (колебательный контур, рис. 2.1, б).
(колебательный контур, рис. 2.1, б).
 Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением
Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением
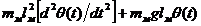
где 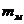 ,
, 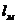 — масса и длина подвеса маятника; g — ускорение свободного падения;
— масса и длина подвеса маятника; g — ускорение свободного падения; 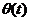 — угол отклонения маятника в момент времени t.
— угол отклонения маятника в момент времени t.
Из этого уравнения свободного колебания маятника можно найти оценки интересующих характеристик. Например, период колебания маятника
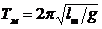
Аналогично, процессы в электрическом колебательном контуре описываются обыкновенным дифференциальным уравнением
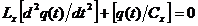
где 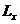 ,
, 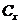 — индуктивность и емкость конденсатора; q(t) — заряд конденсатора в момент времени t.
— индуктивность и емкость конденсатора; q(t) — заряд конденсатора в момент времени t.
Из этого уравнения можно получить различные оценки характеристик процесса в колебательном контуре. Например, период характеристических колебаний
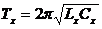
Очевидно, что, введя обозначения 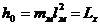 ,
,  ,
, 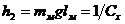 ,
, 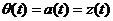 , получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение этой замкнутой системы:
, получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение этой замкнутой системы:
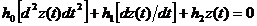 (2.9)
(2.9)
где 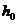 ,
, 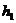 ,
, 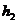 —параметры системы; z (t)— состояние системы в момент времени t.
—параметры системы; z (t)— состояние системы в момент времени t.
Таким образом, поведение этих двух объектов может быть исследовано на основе общей математической модели (2.9). Кроме того, необходимо отметить, что поведение одной из систем может быть проанализировано с помощью другой. Например, поведение маятника (системы 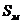 )может быть изучено с помощью электрического колебательного контура (системы
)может быть изучено с помощью электрического колебательного контура (системы 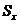 ).
).
Если изучаемая система S, т. е. маятник или контур, взаимодействует с внешней средой E, то появляется входное воздействие x (t) (внешняя сила для маятника и источник энергии для контура)и непрерывно-детерминированная модель такой системы будет иметь вид
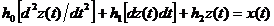
С точки зрения общей схемы математической модели (см. § 2.1) x (t)является входным (управляющим) воздействием, а состояние системы S в данном случае можно рассматривать как выходную характеристику, т. е. полагать, что выходная переменная совпадает с состоянием системы в данный момент времени y=z.
Возможные приложения. При решении задач системотехники важное значение имеют проблемы управления большими системами. Следует обратить внимание на системы автоматического управления — частный случай динамических систем, описываемых D-схемами и выделенных в отдельный класс моделей в силу их практической специфики [24, 43].
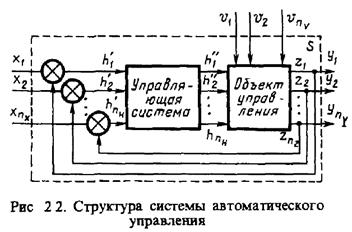
Описывая процессы автоматического управления, придерживаются обычно представления реального объекта в виде двух систем: управляющей и управляемой (объекта управления). Структура многомерной системы автоматического управления общего вида представлена на рис. 2.2, где обозначены эндогенные переменные: 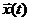 — вектор входных (задающих) воздействий;
— вектор входных (задающих) воздействий; 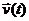 — вектор возмущающих воздействий;
— вектор возмущающих воздействий; 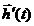 — вектор сигналов ошибки;
— вектор сигналов ошибки; 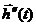 — вектор управляющих воздействий; экзогенные переменные:
— вектор управляющих воздействий; экзогенные переменные: 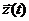 — вектор состояний системы S;
— вектор состояний системы S; 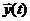 — вектор выходныхпеременных, обычно
— вектор выходныхпеременных, обычно 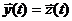 .
.
Современная управляющая система — это совокупность программно-технических средств, обеспечивающих достижение объектом управления определенной цели. Насколько точно объект управления достигает заданной цели, можно судить для одномерной системы по координате состояния 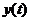 .Разность между заданным
.Разность между заданным 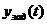 и действительным
и действительным 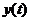 законами изменения управляемой величины есть ошибка управления
законами изменения управляемой величины есть ошибка управления 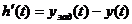 .Если предписанный закон изменения управляемой величины соответствует закону изменения входного (задающего) воздействия, т. е.
.Если предписанный закон изменения управляемой величины соответствует закону изменения входного (задающего) воздействия, т. е. 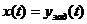 то
то 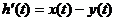 .
.
Системы, для которых ошибки управления 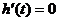 во все моменты времени, называются идеальными Рис 2.2. На практике реализация идеальных систем невозможна. Таким образом, ошибка
во все моменты времени, называются идеальными Рис 2.2. На практике реализация идеальных систем невозможна. Таким образом, ошибка 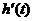 — необходимый субстрат автоматического управления, основанного на принципе отрицательной обратной связи, так как для приведения в соответствие выходной переменной
— необходимый субстрат автоматического управления, основанного на принципе отрицательной обратной связи, так как для приведения в соответствие выходной переменной 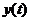 ее заданному значению используется информация об отклонении между ними. Задачей системы автоматического управления является изменение переменной
ее заданному значению используется информация об отклонении между ними. Задачей системы автоматического управления является изменение переменной 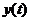 согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы S, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы S, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной 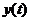 в переходном процессе, время переходного процесса и т. п. Выводы о свойствах систем автоматического управления различных классов можно сделать по виду дифференциальных уравнений, приближенно описывающих процессы в системах. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы S.
в переходном процессе, время переходного процесса и т. п. Выводы о свойствах систем автоматического управления различных классов можно сделать по виду дифференциальных уравнений, приближенно описывающих процессы в системах. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы S.
Пример 2.1. Рассмотрим одноканальную систему автоматического управления 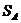 , которая описывается D-схемой общего вида
, которая описывается D-схемой общего вида
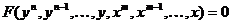 (2.10)
(2.10)
где 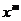 и
и 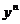 — производные по времени m -го и n -го порядков от функции х и у соответственно. Пусть система
— производные по времени m -го и n -го порядков от функции х и у соответственно. Пусть система 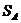 , описываемая уравнением (2.10), работает в некотором режиме, характеризуемом функциями
, описываемая уравнением (2.10), работает в некотором режиме, характеризуемом функциями 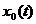 н
н 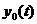 .Обозначим малые отклонения
.Обозначим малые отклонения 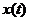 от
от 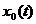 через
через 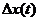 , a
, a 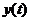 от
от 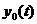 через
через 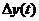 , т. е.
, т. е. 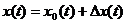 ,
, 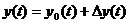 .
.
Тогда уравнение (2.10) можно линеаризовать, разложив функцию 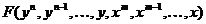 в ряд Тейлора и ограничившись его линейными членами относительно приращений
в ряд Тейлора и ограничившись его линейными членами относительно приращений 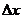 и
и 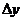 т. е.
т. е.
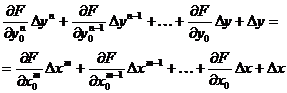 (2.11)
(2.11)
Так как полученное уравнение (2.11) приближенно описывает рассматриваемый процесс, то производные вычисляют при некоторых фиксированных значениях входящих в него переменных, т. е. получается система с постоянными коэффициентами. Кроме того, уравнения получаются линейными относительно 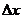 ,
, 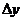 и их производных. Это весьма существенно, так как методы решения и исследования линейных систем значительно проще, чем систем общего вида, и более детально разработаны
и их производных. Это весьма существенно, так как методы решения и исследования линейных систем значительно проще, чем систем общего вида, и более детально разработаны
Таким образом, для линейных систем автоматического управления, т. е. для систем, описываемых линейными дифференциальными уравнениями, можно записать
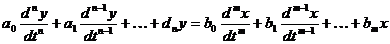 (2.12)
(2.12)
В уравнении (2.12) для простоты предполагается, что точки приложения возмущающих воздействий совпадают с входом системы. Для решения (2.12) можно воспользоваться, например, операторным методом, заменяя дифференциальное уравнение алгебраическим.
Таким образом, использование D-схем позволяет формализовать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход, реализованный в виде соответствующего языка для моделирования непрерывных систем или использующий аналоговые и гибридные средства вычислительной техники.
 2017-12-16
2017-12-16 683
683








