Фазовые траектории нелинейных систем. Устойчивые и неустойчивые предельные циклы

1. Фазовые траектории нелинейных систем.

Фазовые траектории нелинейных САУ могут быть получены путем приближенного интегрирования дифференциальных уравнений. Если Р и Q - кусочно-линейные функции, то система:

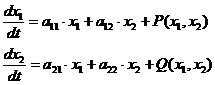…(5.59)

представляет собой ряд подсистем линейных дифференциальных уравнений, каждая из которых справедлива в определенной области плоскости . В каждой области фазовые траектории могут быть определены как часть траекторий соответствующей линейной системы; сшиванием траекторий, принадлежащих областям , находятся траектории на всей плоскости .

Для линейных систем факт сходимости процессов к состоянию равновесия не зависит от начальных условий. В нелинейных системах возможны более сложные случаи, когда переходные процессы сходятся к состоянию равновесия при одних и расходятся при других начальных условиях. Если переходный процесс сходится к состоянию равновесия при малых отклонениях от этого состояния и расходится в бесконечность при больших отклонениях, то границей между областями сходимости и расходимости на фазовой плоскости обычно служит замкнутая траектория, соответствующая периодическому процессу, рис. 5.22.

Рис. 5.22. Фазовая траектория.

Такую изолированную замкнутую траекторию называют предельным циклом. При сколь угодно малом начальном отклонении от этой траектории изображающая точка уходит либо к началу координат, либо в бесконечность. Поэтому периодическое движение в данном случае неустойчиво, а соответствующий ему на фазовой плоскости предельный цикл носит название неустойчивого предельного цикла.

В нелинейных системах возможны и устойчивые предельные циклы, на которые фазовые траектории асимптотически наматываются изнутри и снаружи, рис. 5.23. На фазовом портрете, изображенном на рис. 5.23, состояние равновесия системы при неустойчиво. Все движения системы, независимо от величины начальных отклонений, заканчиваются стационарными колебаниями вполне определенного характера.

Рис. 5.23. Фазовый портрет.

В нелинейных системах возможны случаи, когда одновременно имеется несколько предельных циклов, устойчивых и неустойчивых. Предельные циклы, также как и отрезки покоя, являются примерами особых линий на фазовой плоскости.

Возможен также случай более удаленного предельного цикла, рис. 5.24, соответствующий автоколебаниям с большой амплитудой.

Рис. 5.24. Фазовый портрет.

Такие же принципиальные качественные изменения картины фазовых траекторий при достаточно больших отклонениях могут наблюдаться и в случаях апериодических процессов, включая превращения их в колебательный и наоборот, рис. 5.25.

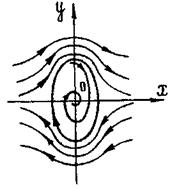
Рис. 5.25. Фазовые траектории

Аналогично для системы, находящейся согласно линейной теории на границе устойчивости (при чисто мнимых корнях), картина фазовых траекторий при больших отклонениях, если линейность характеристик звеньев системы нарушается возможен вариант изменения фазовых траекторий при больших отклонениях, как это показано на рис. 5.26. Здесь, кроме особой точки 0 типа центра, появляются два седла 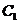и , что приводит фактически к неустойчивости системы. Но может иметь место и предельный цикл. Особые линии такого типа, как и , на фазовой плоскости называются сепаратриссами.

Рис. 5.26. Фазовые траектории.

Здесь говорилось пока о системах, которые при малых отклонениях рассматриваются как линейные. Но совершенно аналогичная картина получается и для нелинейных САУ, которые даже в малом нельзя рассматривать как линейные. Таковыми являются многочисленные типы релейных систем, а также систем с зоной нечувствительности, с гистерезисной петлей, с сухим трением, с зазором. Интересно отметить, что некоторые из таких систем скорее в большом, чем в малом, могут приблизиться к линейным, когда зона нечувствительности или зазор оказываются малыми по сравнению с величиной отклонений.

В системах с зоной нечувствительности и с сухим трением существуют, как известно, области застоя, когда установившемуся состоянию при данных внешних условиях соответствует не одна точка, а целая область возможных равновесных состояний системы. На фазовой плоскости это выражается в особый отрезок, рис. 5.27.

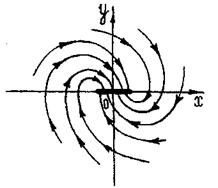
Рис. 5.27. Фазовые траектории.

Заметим, наконец, что координатами фазовой плоскости могут служить не обязательно отклонения управляемой величины и скорость ее, как рассмотрено выше. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени.

2. Автоколебания нелинейных систем.

В реальных САУ наблюдаются периодические движения, называемые автоколебаниями и обладающие следующими особенностями.

Первым признаком того, что данное незатухающее колебание относится к автоколебаниям, является отсутствие периодического внешнего воздействия: автоколебания являются собственными колебаниями системы. Форма и частота автоколебаний не зависит от начальных условий. Автоколебания, устанавливающиеся в данной системе после окончания переходных процессов, имеют вполне определенную форму и частоту, которые могут быть изменены лишь изменением параметров системы, т.е. коэффициентов уравнений движения системы.

Наконец, характерной особенностью автоколебаний является то обстоятельство, что они обычно не исчезают при достаточно малых изменениях начальных условий и параметров системы. Точнее, если автоколебания существуют, то они существуют для целой области начальных отклонений. И если автоколебания возникают при каких-то определенных параметрах системы, то они возникают и при других, близких к ним, значениях параметров, несколько меняясь при этом по форме и частоте.

Для теории автоматического управления изучение автоколебаний весьма существенно, так как в большинстве своем САУ в равной степени могут работать и как системы стабилизации и как автоколебательные системы: они обычно являются потенциально автоколебательными системами. Часто конструкторам приходится затрачивать много времени и труда, чтобы устранить автоколебания. Но иногда наоборот автоколебательные режимы являются нормальными режимами работы системы, если это позволяют условия процесса управления.

САУ, где амплитуда выходного параметра управления не превышает допустимой величины, называются практически устойчивыми. Если же амплитуда автоколебаний настолько велика, что система становится неудовлетворительной по требованию качества, ее считают практически неустойчивой.

В отдельных случаях автоколебания позволяют добиться определенных положительных свойств, в частности, уничтожить застой в зоне нечувствительности. Благодаря непрерывным колебаниям обеспечивается режим динамической смазки в гидравлических системах.

При проектировании нелинейных систем важно определить допустимые значения амплитуды и частоты автоколебаний, а также характер влияния отдельных параметров системы на изменение амплитуды и частоты, чтобы достигнуть требуемых свойств автоколебательного режима.

3. Коррекция нелинейных САУ.

Для улучшения процесса управления в нелинейных САУ также, как и в линейных САУ, используют корректирующие цепи. Благодаря применению корректирующих устройств удается добиться устойчивости системы, устранить или снизить до практически допустимых значений автоколебания и улучшить качество переходного процесса.

В нелинейных САУ находят применение:

- Последовательные корректирующие цепи, позволяющие осуществить введение в закон управления производных и интегралов.

- Параллельные корректирующие цепи в виде различных жестких и гибких обратных связей.

- Корректирующие устройства, с помощью которых осуществляется введение в закон управления сигналов, пропорциональных возмущающему моменту.

§ 8.5. Точные методы исследования устойчивости нелинейных САУ.

1. Прямой (второй) метод Ляпунова.

Уравнения САУ в форме Коши имеют вид (в отклонениях):

…(5.62).

- произвольные функции, содержащие любые нелинейности;

- отклонения переменных САУ, удовлетворяющие условию:

;

Пусть имеется функция нескольких переменных , которая обращается в нуль в начале координат, т.е. при 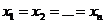и непрерывна в некоторой области вокруг него.

1. Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и не обращается в нуль, кроме только самого начала координат.

2. Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

3. Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

1.1. Функция Ляпунова и ее производная во времени.

Любую функцию , тождественно обращающуюся в нуль при , будем называть функцией Ляпунова, если в ней в качестве величин 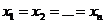взяты те отклонения переменных САУ в переходном процессе , в которых записываются уравнения Коши для этой системы.

Производная от функции Ляпунова по времени будет:

…(5.63). Подставив вместо - значения из уравнении Коши, получим:

или 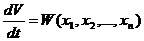…(5.64).

Следовательно, производная от функции Ляпунова по времени, так же, как и сама функция V, является некоторой функцией отклонений переменных САУ. Поэтому к ней применимы понятия знакоопределенности, знакопостоянства и знакопеременности.

1.2. Теорема Ляпунова.

Если в заданных в форме Коши уравнениях системы n -ого порядка можно подобрать такую знакоопределенную функцию Ляпунова , чтобы ее производная по времени тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива.

При знакоопределенной W будет асимптотическая устойчивость.

Для простоты возьмем САУ 3-го порядка:

…(5.65).

- знакоопределенная положительная; - произвольно заданные положительные вещественные числа.

Будем предавать величине V возрастающие постоянные значения 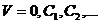V = О, С,, С₂,..., что означает:

…(5.66).

Возьмем производную по времени от V:

Если 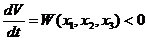- знакоопределенная во всех точках фазового пространства, кроме начала координат, где , то при любых начальных условиях изображающая точка М (рис. 5.32) будет двигаться в сторону уменьшения значения V, т.е. будет пересекать эллипсоиды, изображенные на рисунке извне - внутрь.

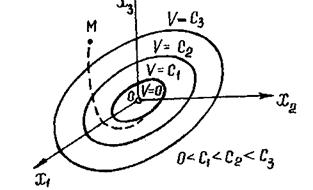
Рис. 5.32. Функция Ляпунова.

В результате с течением времени изображающая точка М будет стремиться к началу координат фазового пространства и уже не сможет выйти за пределы тех эллипсоидов, внутрь которых она проникла.

Это означает затухание всех отклонений в переходном процессе с течением времени.

Это говорит об устойчивости САУ в случае знакоопределенной отрицательной W.

Если W будет знакопостоянной, то траектория изображающей точки не везде будет пересекать поверхности , а может их касаться в тех точках, где W обращается в ноль. В этом случае необходимо проверить, не застрянет ли она в этой точке, что определит для САУ наличие предельного цикла.

1.3. Теорема Ляпунова о неустойчивости нелинейных САУ.

Если при заданных уравнениях САУ в форме Коши производная 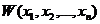от какой-то функции Ляпунова окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.

Пусть при

…(5.67) оказалась знакоопределенно положительной.

Пусть при этом линии на фазовой плоскости располагаются так, как показано на рис. 5.33, где линии АВ и CD соответствуют значениям и разделяют те области, внутри которых и .

Рис. 5.33. Функция Ляпунова.

В точке М, поскольку V < 0 и везде , то точка М будет стремиться и пересекать , переходя от меньших значений С к большим.

Она может временно приближаться к началу координат, но в конце концов будет удаляться от начала координат. Это соответствует расходящемуся процессу, т.е. неустойчивой системе.

2. Частотный метод В.М.Попова.

Если в САУ имеется лишь одна нелинейность , то, объединив вместе все остальные линейные уравнения системы, можно всегда получить общее уравнение линейной части САУ в виде (рис. 5.34): , где:

; ; .

Рис. 5.34. Представление нелинейной САУ.

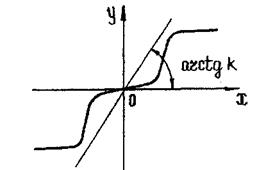
Рис. 5.35. Очертание нелинейности.

Пусть нелинейность имеет любое очертание, не выходящее за пределы угла (рис. 5.35), т.е. при любом х: , тогда:

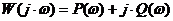; …(5.68).

Допускается, чтобы в выражении Q(S) было не более двух нулевых полюсов.

2.1. Теорема В.М. Попова.

Для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, при котором при всех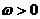

, где и - видоизмененные части вещественной и мнимой частей передаточной функции , при этом:

, …(5.69);

…(5.70).

График 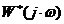имеет вид, аналогичный , когда в выражениях Q(S) и R(S) разность степеней (рис. 5.36 а).

Если же разность степеней 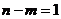, то конец графика 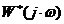будет на мнимой оси ниже начала координат (рис. 5.36 б).

Рис. 5.36. Графики .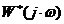

Очевидно, что равенство …(5.71) представляет уравнение прямой на плоскости .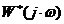

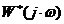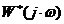Отсюда вытекает графическая интерпретация теоремы В.М.Попова: для установления устойчивости нелинейной САУ достаточно подобрать такую прямую на плоскости , проходящую через точку (), чтобы вся кривая лежала справа от этой прямой.