Точки перегиба графика функции

Общая схема исследования функции и построение графика.

1. Исследование функции на выпуклость и вогнутость.

2. Точки перегиба графика функции.

3. Асимптоты графика функции.

4. Схема полного исследования функции и построение графика.

Введение.

В школьном курсе математики вы уже встречались с необходимостью построения графиков функций. В основном, вы использовали способ построения по точкам. Следует отметить, что он прост по идее и сравнительно быстро приводит к цели. В случаях, когда функция непрерывна и изменяется довольно плавно, такой способ может обеспечить и необходимую степень точности графического представления. Для этого нужно брать побольше точек, чтобы достичь определённой густоты их размещения.

Предположим теперь, что функция в отдельных местах имеет особенности в своём «поведении»: либо её значения где-то на малом участке резко меняются, либо имеют место разрывы. Наиболее существенные части графика таким способом могут и не быть обнаружены.

Это обстоятельство и снижает ценность способа построения графика «по точкам».

Существует второй способ построения графиков, основанный на аналитическом исследовании функций. Он выгодно отличается от способа, рассмотренного в школьном курсе математики.

1. Исследование функции на выпуклость и вогнутость.

Пусть функция дифференцируема на интервале (а, в). Тогда существует касательная к графику функции в любой точке этого графика (), причем касательная не параллельна оси OY, так как ее угловой коэффициент, равный , конечен.

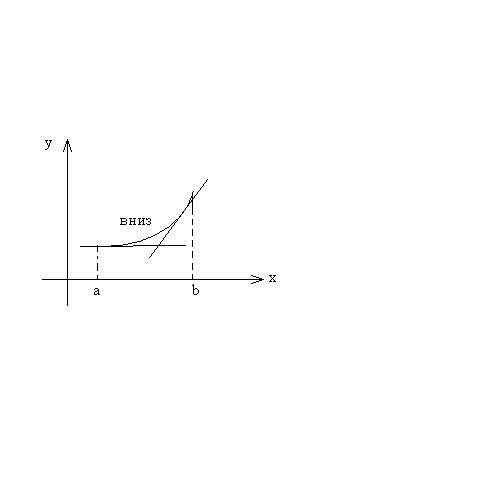
Определение Будем говорить, что график функции на (а, в) имеет выпускать, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а, в).

 

 

а) вогнутая кривая б) выпуклая кривая

Теорема 1 (необходимое условие выпуклости (вогнутости) кривой).

Если график дважды дифференцируемой функции выпуклая (вогнутая) кривая, то вторая производная на интервале (а, в) отрицательна (положительна) на этом интервале.

 

Теорема 2 (достаточное условие выпуклости (вогнутости) кривой).

Если функция дважды дифференцируема на (а, в) и () во всех точках этого интервала, то кривая, являющаяся графиком функции выпуклая (вогнутая) на этом интервале.

Точки перегиба графика функции.

Определение Точка называется точкой перегиба графика функции , если в точке график имеет касательную, и существует такая окрестность точки , в пределах которой график функции слева и справа точки имеет разные направления выпуклости.

Очевидно, что в точке перегиба касательная пересекает график функции, так как с одной стороны от этой точки график лежит над касательной, а с другой – под нею, т. е. в окрестности точки перегиба график функции геометрически переходит с одной стороны касательной на другую и «перегибается» через нее. Отсюда и произошло название «точки перегиба».

 

Теорема 3 (необходимое условие точки перегиба). Пусть график функции имеет перегиб в точке и пусть функция имеет в точке непрерывную вторую производную. Тогда .

 

Не всякая точка , для которой , является точкой перегиба. Например, график функции не имеет перегиба в точке (0, 0), хотя при . Поэтому равенство нулю второй производной является лишь необходимым условием перегиба.

Точки графика, для которых называется критическими точками II-го рода. Необходимо дополнительно исследовать вопрос о наличии перегибав каждой критической точке.

Теорема 4 (достаточное условие точки перегиба). Пусть функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах указанной окрестности имеет разные знаки слева и справа от точки , то график имеет перегиб в точке .

 

Замечание. Теорема остается верной, если имеет вторую производную в некоторой окрестности точки , за исключением самой точки , и существует касательная к графику функции в точке . Тогда, если в пределах указанной окрестности имеет разные знаки слева и справа от точки , то график к функции имеет перегиб в точке .