Асимптоты графика функции. При исследовании поведения функции при или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или

При исследовании поведения функции при 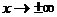или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют.

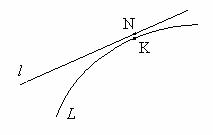
Определение 1. Прямая 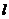называется асимптотой кривой L, если расстояние от точки кривой до этой прямой стремится к нулю при удалении точки по кривой к бесконечности. Существует три вида асимптот: вертикальные, горизонтальные, наклонные.

Определение 2. Прямая 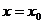называется вертикальной асимптотой графика функции , если хотя бы один из односторонних пределов равен 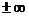, т. е. или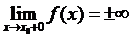

Например, график функции 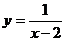имеет вертикальную асимптоту 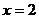, т. к. 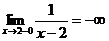, а .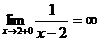

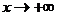Определение 3. Прямая у=А называется горизонтальной асимптотой графика функции при если .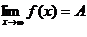

Например, график функции 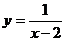имеет горизонтальную асимптоту у=0, т. к. .

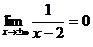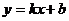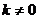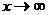Определение 4. Прямая () называется наклонной асимптотой графика функции при если ;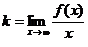

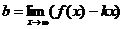
Если хотя бы один из пределов не существует, то кривая асимптот не имеет. Если, то следует искать эти пределы отдельно, пр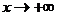и и .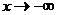

Например. Найти асимптоты графика функции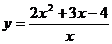

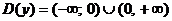
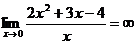; х=0 – вертикальная асимптота

; .

;

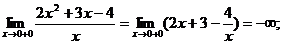
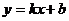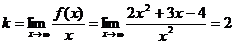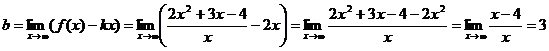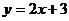- наклонная асимптота.