2017-12-16
964
Рассмотрим примерную схему по которой целесообразно исследовать поведение функции и строить ее график.
1. Найти область определения функции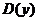 
.
2. Проверить функцию на четность и нечетность
3. Найти асимптоты.
4. Найти точки возможного экстремума, т. е. критические точки I – го рода.
5. Найти точки возможного перегиба, т. е. критические точки II-го рода.
6. Составить сводную таблицу.
7. Найти точки пересечения графика функции с осями координат
8. Построить график функции, учитывая проведенное исследование.
9.
Пример. Исследовать функцию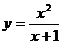 
и построить ее график.
1. 
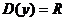, кроме х=-1.
2. 
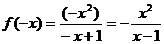функция ни четная ни нечетная
3. 
; 
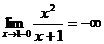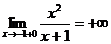; х=-1 точка разрыва функции 2 – го рода, а прямая х=-1 – вертикальная асимптота.
; 
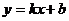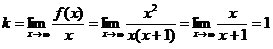
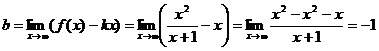
Следовательно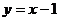 
наклонная асимптота
4. 
; 
; 
; 
; 
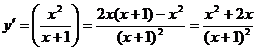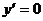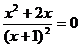
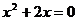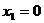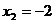- критические точки I-го рода
5. 
= 
;
; 
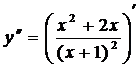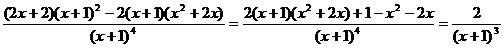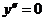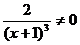критических точек второго рода нет.
| 
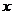
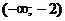
| -2 |  ( )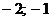
| -1 | (-1; 0) |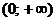 
| |||||||
| y’ | + | - |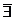 
| - | + | ||||||||
| - | - |
| + | + | ||||||||
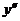
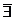
| y |
| -4 |
| т р. |
|
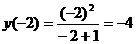
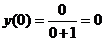
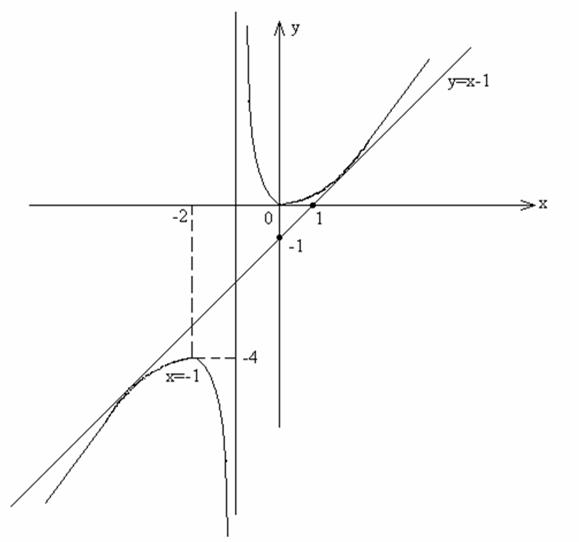
Заключение.
|
|
|
Важной особенностью рассмотренного способа является то, что в его основе лежит прежде всего обнаружение и изучение характерных особенностей в поведении кривой. Места, где функция изменяется плавно, не изучаются особенно подробно, да и нет надобности в таком изучении. Зато те места, где функция имеет какие-либо особенности в поведении, подлежат полному исследованию и максимально точному графическому изображению. Этими особенностями являются точки максимума, минимума, точки разрыва функции и др.
Определение направления вогнутости и перегибов, а также указанный способ нахождения асимптот дают возможность провести исследование функций ещё более детально и получить более точное представление об их графиках.
