2017-12-16
471
а) Пусть 
- функция двух переменных х и у, каждая из которых является функцией независимой переменной t, т.е.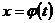 
, 
.
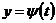Тогда функция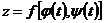 
является сложной функцией 
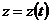независимой переменной t. Переменные х и у являются промежуточными аргументами.
Предположим, что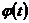 
и 
дифференцируемые функции. Придадим переменной t приращение Δt, тогда 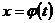и 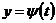получат соответственно приращения Δх и Δу и приращение Δz будет иметь вид:
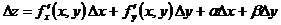, где
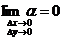и 
Разделим Δz на Δt:
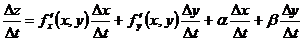
и перейдём к пределу при Δt→0:
=
= 
.
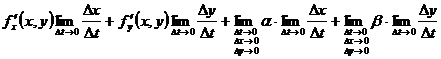Из дифференцируемости функци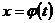й и 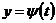, следует их непрерывность, т.е. 
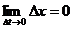и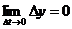 
.
Следовательно,
; 
.
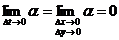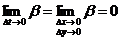Таким образом,
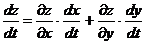(1)
Пример.
, 
, 
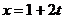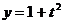
Решение.
; 
; 
; 
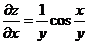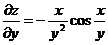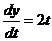
Итак,
- 
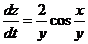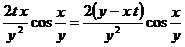
Замечание. Если , где 
, то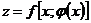 
- сложная функция одной переменной. Тогда
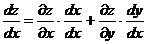или
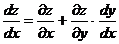(2)
Производную (2) называют полной производной функции .
Пример.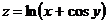 
, 
Решение.
; 
; 
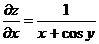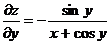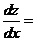
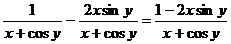
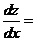
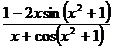
Проверка. Имеем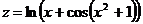 
= .
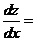
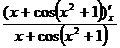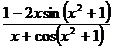б) Пусть , где 
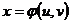и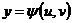 
. Функция 
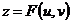является сложной функцией независимых переменных u и v, а переменные х и у называют промежуточными аргументами.
Предположим, что все функции дифференцируемые. Чтобы найти 
, надо считать, что v=const. Тогда х и у становятся функциями только одной переменной и мы приходим к рассмотренному случаю. Разница только в том, что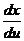 
и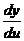 
заменяются частными производным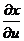и 
и 
.
Таким образом,
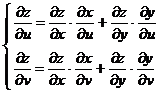(3)
Пример. ; 
; 
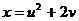Решение.
;
; 
;
; 
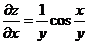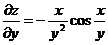
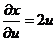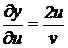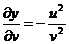
Имеем
= 
- 
= 
- 
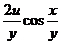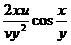
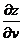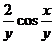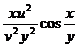
4. Инвариантность формы полного дифференциала.
Если х и у – независимые переменные, то полный дифференциал функции имеет вид
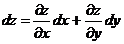(4)
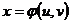Пусть и 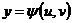, тогда и функция z является функцией независимых переменных u и v:
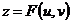
По определению полного дифференциала на основании равенства (4) имеем
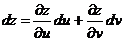
Учитывая формулы (3), получим
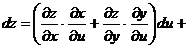
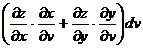
Раскроем скобки и вынесем за скобк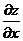и 
и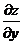 
:
;
Учитывая, что
,
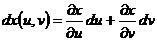
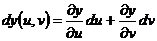получим
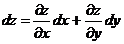(5)
Сравнивая равенства (4) и (5) делаем вывод.
Дифференциал функции сохраняет один и тот же вид независимо от того, являются ли её аргументы х и у независимыми переменными или функциями независимых переменных.
Таким образом, для функции 2-х переменных имеет место свойство инвариантности формы полного дифференциала.
Для функции 2-х переменных имеют место правила дифференцирования, выраженные следующими формулами:
1) 
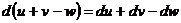
2) 
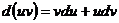
3) 
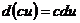, где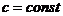 
4) 
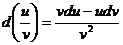
5) 
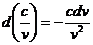, где ,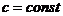
где u,v,w – функции любого числа переменных.
Пример.
; ;
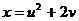Решение.
( - ) 
( - ) 
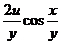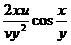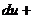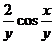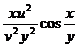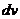
Или, учитывая, что
, 
(
) - 
(
)=
=( - ) ( - ) .
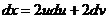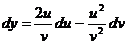
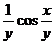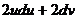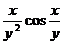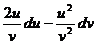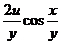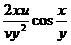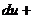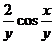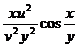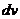Заключение.
Важной частью исследования функций является локальное исследование, под которым понимается сравнение значения функции в данной точке со значениями функции в точках, близких к данной. Всё изложение данной лекции было проведено на примере функции двух переменных, это позволяет сделать обсуждение геометрически наглядным. Следует заметить, что каждое утверждение о функции двух переменных, которое было приведено, без труда обобщается на случай функции п -переменных.
