2017-12-16
668
а) Применение полного дифференциала для вычисления функций.
Из определения полного дифференциала функции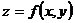 
с точностью до бесконечно малых высшего порядка малости относительно 
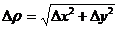можно записать приближённое равенство: 
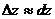или
+ 
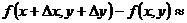
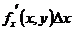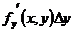, отсюда
+ +
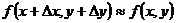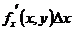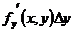
или +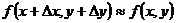 
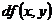
Последняя формула используется в приближённых вычислениях для нахождения значений функции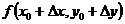 
, близких к значению функции 
.
+ 
.
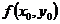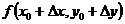
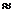
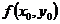Пример: Вычислить 1,033,001
= 
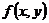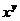, х0=1, у0=3,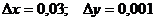 
+
= 
+ 
, 
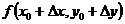
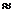
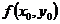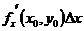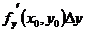
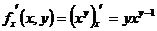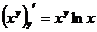
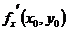=3·12=3, 
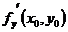=13·ln1=0
=3·0,03+0·0,001=0,09
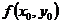=13=1
Таким образом 1,033,001 1+0,09=1,09
б) Применение дифференциала при оценке погрешности вычислений.
Пусть некоторая величина u является функцией величин х и у, т.е.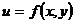 
. При определении величин х и у были допущены погрешности ∆ х и ∆ у соответственно.
Тогда значение величины u, вычисленное по неточным значениям аргументов, получится с погрешностью
∆ и=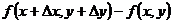 
Но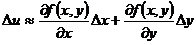 
Значения частных производных и значения ∆ х и ∆ у могут быть как положительными, так и отрицательными. Заменяя их абсолютными величинами, получим неравенство:
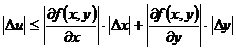
Если через 
и 
обозначить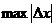 
и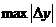 
- границы для абсолютных погрешностей величин х и у, то максимальная абсолютная погрешность 
величины и примет вид
отношение абсолютной погрешности ∆ и величины и к приближенному значению и этой величины называется относительной погрешностью этой величины.
Обозначение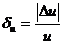 
.
Максимальной относительной погрешностью величины и называется отношение максимальной абсолютной погрешности к абсолютной величине и и обозначается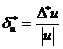 
Следовательно
= 
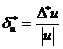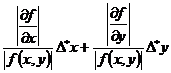
Учитывая, что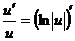 
, будем иметь
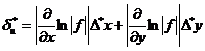
или
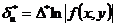
Максимальная относительная погрешность функции равняется максимальной абсолютной погрешности логарифма этой функции.
Пример: Наклонная дальность НД связана с высотой полета h и углом
визирования β зависимостью:
НД=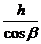 
Условия определения НД: h=10000м., β=600. Определить
максимальную абсолютную погрешность и максимальную
относительную погрешность при изменении НД, если высота
полета измеряется с максимальной абсолютной погрешностью
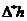=150м., а угол визирования – с максимальной абсолютной
погрешностью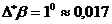 
рад.
Решение:
; 
= 
; 
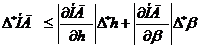
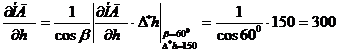
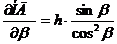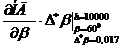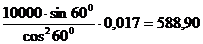
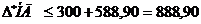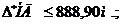
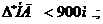
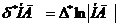
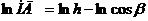
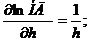
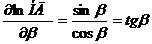
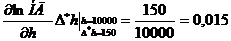
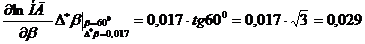
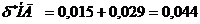
Итак,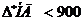 
м. 
%
