Введение.
Пусть дана функция одной переменной 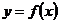 , имеющая производную. Дифференциал этой функции вычисляется по формуле
, имеющая производную. Дифференциал этой функции вычисляется по формуле 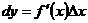 . Таким образом понятие дифференциала определено для всякой функции, имеющей производную, и поэтому выражение «функция
. Таким образом понятие дифференциала определено для всякой функции, имеющей производную, и поэтому выражение «функция 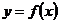 дифференцируема» означает как то, что она имеет производную, так и то, что она имеет дифференциал.
дифференцируема» означает как то, что она имеет производную, так и то, что она имеет дифференциал.
В случае функции нескольких переменных дело обстоит по-другому: существование частных производных является необходимым условием дифференцируемости функции в точке, но не является достаточным условием. Дифференцируемость имеет место, если дополнительно потребовать непрерывность частных производных.
Полное приращение функции. Полный дифференциал.
Придадим аргументу 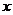 приращение
приращение 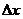 , а аргументу
, а аргументу 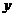 приращение
приращение 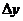 , получим полное приращение функции
, получим полное приращение функции 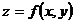 , которое обозначается
, которое обозначается 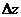 :
:
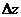 =
= 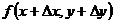 -
- 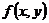
Предположим, что 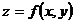 в точке
в точке 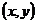 имеет непрерывные частные производные
имеет непрерывные частные производные 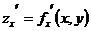 и
и 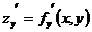 .
.
Выразим полное приращение 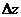 через частные производные. Для этого в правой части записанного равенства вычтем и прибавим
через частные производные. Для этого в правой части записанного равенства вычтем и прибавим 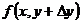 :
:
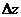 =
= 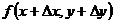 -
- 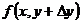 +
+ 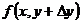 -
- 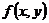
Выражения 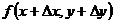 -
- 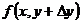 и
и 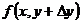 -
- 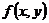 можно рассматривать как разности 2-х значений функций одной переменной. Применяя к этим разностям теорему Лагранжа, получим
можно рассматривать как разности 2-х значений функций одной переменной. Применяя к этим разностям теорему Лагранжа, получим 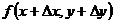 -
- 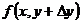 =
= 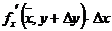 , где
, где 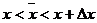 ;
;
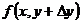 -
- 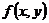 =
= 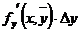 , где
, где 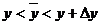 .
.
Тогда 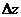 =
= 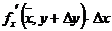 +
+ 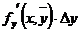 .
.
Если 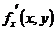 и
и 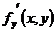 - непрерывны, то
- непрерывны, то 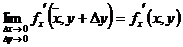 ;
;
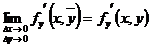 , тогда
, тогда 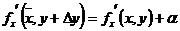
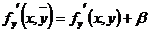
где 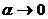 и
и 
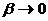 , если
, если 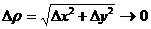
Следовательно,
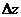 =
= 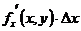 +
+ 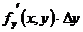 +
+ 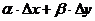
Сумма 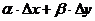 является бесконечно малой высшего порядка относительно
является бесконечно малой высшего порядка относительно 
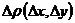 :
: 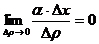 и
и 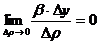 , так как
, так как 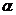 и
и 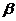 - бесконечно малые, а
- бесконечно малые, а
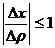 и
и 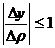 .
.
Выражение 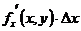 +
+ 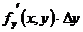 - линейное относительно
- линейное относительно 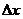 и
и 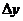 и представляет собой главную часть приращения
и представляет собой главную часть приращения 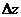 , отличаясь от
, отличаясь от 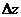 на бесконечно малую высшего порядка относительно
на бесконечно малую высшего порядка относительно 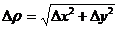 .
.
Определение: Главная часть полного приращения 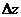 функции
функции 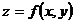 ,
,
линейная относительно приращений аргументов 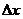 и
и 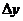 ,
,
называется полным дифференциалом этой функции.
Обозначается полный дифференциал 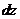 или
или 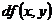 .
.
По определению 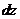 =
= 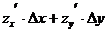 или
или 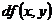 =
= 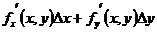
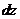 =
= 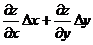
Учитывая, что 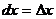 ,
, 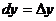 , можно записать
, можно записать
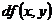 =
= 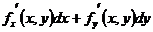 или
или 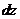 =
= 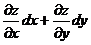 .
.
Определение: Функция 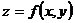 полное приращение которой в точке
полное приращение которой в точке 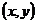
может быть представлено в виде
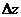 =
= 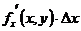 +
+ 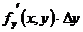 +
+ 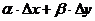 ,
,
называется дифференцируемой в данной точке.
Из определения следует, что наличие у функции 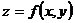 полного дифференциала обеспечивает существование у этой функции частных производных в точке
полного дифференциала обеспечивает существование у этой функции частных производных в точке 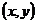 .
.
Из существования у функции 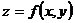 в некоторой точке
в некоторой точке 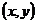 частных производных не следует её дифференцируемость в этой точке, т.е. наличие у этой функции полного дифференциала. Условие дифференцируемости функции двух переменных устанавливает следующая теорема.
частных производных не следует её дифференцируемость в этой точке, т.е. наличие у этой функции полного дифференциала. Условие дифференцируемости функции двух переменных устанавливает следующая теорема.
Теорема: Если функция 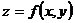 имеет в точке М
имеет в точке М 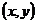 непрерывные
непрерывные
частные производные 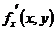 и
и 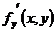 , то в этой точке функция
, то в этой точке функция
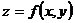 дифференцируема. Из дифференцируемости функции
дифференцируема. Из дифференцируемости функции
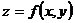 в точке М
в точке М 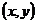 следует
следует
1) её непрерывность в этой точке;
2) существование в этой точке её частных производных 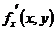 и
и
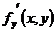 .
.
Пример: Найти 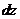 функции
функции 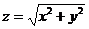 .
.
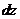 =
= 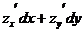
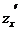 =
= 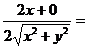
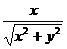 ;
; 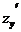 =
= 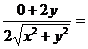
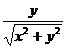
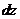 =
= 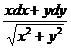 .
.
Выражения 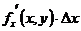 или
или 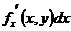 и
и 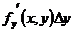 или
или 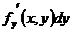 называют частными дифференциалами по х и по у соответственно функции
называют частными дифференциалами по х и по у соответственно функции 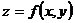 в точке
в точке 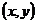 и обозначают
и обозначают 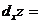
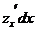 и
и 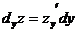 или
или
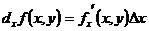 и
и 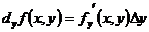 .
.
Следовательно, 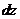 =
= 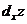 +
+ 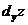 или
или 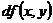 =
= 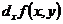 +
+ 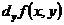 .
.
 2017-12-16
2017-12-16 2194
2194