Нахождение наибольшего паросочетания в двудольном графе

 

Граф G = (V,X) называется двудольным, если множество V его вершин допускает разбиение на два непересекающихся подмножества V₁ и V₂ (две доли), причем каждое ребро графа соединяет вершины из разных долей.

Обозначим G = (V₁,V₂, X) двудольный граф G с долями V₁ и V₂. Будем считать, что çV₁ç£ çV₂ç.

Двудольный граф G = (V₁,V₂, X) есть полный двудольный граф, если каждая вершина из V₁ соединена ребром с каждой вершиной из V₂.

Паросочетанием Р для двудольного графа G=(V₁,V₂,X) называется любое множество попарно несмежных ребер в G.

Р есть наибольшее паросочетание для G, если число ребер в Р наибольшее среди всех возможных паросочетаний для G.

Р есть максимальное паросочетание (тупиковое) для G, если к Р нельзя добавить ни одного ребра из G, не нарушив условия паросочетаемости.

Р есть совершенное паросочетание для G, если Р имеет çV₁ç ребер.

Наибольшее паросочетание максимально. Совершенное паросочетание является и наибольшим, и максимальным.

Рассмотрим задачу нахождения наибольшего паросочетания в заданном двудольном графе. Это классическая задача комбинаторики, известная также под названием «задачи о назначениях».

Оказывается, что задачу нахождения наибольшего паросочетания в двудольном графе можно свести к задаче построения максимального потока в некоторой сети.

Пусть G=(V₁,V₂,X) – произвольный двудольный граф. Построим сеть S(G) с источником s, стоком t (s¹t, s,tÏV₁ÈV₂,), множеством вершин

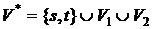, множеством дуг

,

и пропускной способностью c(u,v)=1 для каждой дуги (u,v) ÎX’.

На рис.3 показано построение сети S(G) для некоторого двудольного графа.Отметим, что в сети S(G) существует максимальный нуль-единичный поток, т.е. максимальный поток φ такой, что φ(x)=0 или φ(x)=1 для каждой дуги xÎX’.

Теорема. Существует взаимно однозначное соответствие между паросочетаниями в G и нуль-единичными потоками в S(G), при котором паросочетанию M={(v₁,u₁), …(v_k,u_k)} мощности k (v_iÎV₁, u_iÎV₂ для 1£ i £ k) соответствует поток φ_М величины k, определяемый следующим образом:

 

φ_М (s,v_i) = φ_М (v_i,v_j)= φ_М (v_j,t)=1, 1£i£ k,

 

и φ_М (x)=0 для остальных дуг x сети S(G); потоку φ величины k соответствует паросочетание М_φ, |М_φ|=k, определяемое следующим образом:

 

М_φ = {(v,u)| vÎV₁ & uÎV₂ & φ(v,u)=1}.

 

Данная теорема позволяет использовать произвольный алгоритм построения максимального потока (целочисленного) для определения наибольшего паросочетания.

 

Рис.3.

 

ЗАДАНИЕ 24. Решить задачу нахождения наибольшего паросочетания в двудольном графе, сведя ее к задаче построения максимального потока в транспортной сети и используя первый алгоритм построения максимального потока.

ЗАДАНИЕ 25. Решить задачу нахождения наибольшего паросочетания в двудольном графе, сведя ее к задаче построения максимального потока в транспортной сети и используя алгоритм меток для построения максимального потока.

 

Замечание. Двудольный граф задавать в виде матрицы смежности, строки которой соответствуют вершинам первой доли, а столбцы – вершинам второй доли.