Теоретические основы лабораторной работы

Описание установки

Приборы и принадлежности, используемые в лабораторной работе, показаны на рисунке 1. Для питания моделей используется стабилизированный источник 1 постоянного напряжения. Для измерения потенциала – цифровой вольтметр 2 с большим внутренним сопротивлением (не менее 1Мом). Для исследования распределения потенциала используется плоские планшеты 3. В каждом планшете на изолирующей жесткой подложке наклеены металлические электроды из медной фольги и слой проводящей бумаги между электродами. Для подсоединения к источнику питания, каждый планшет снабжен проводами с однополюсными вилками на концах. Координаты щупа на планшете, моделирующем плоский конденсатор, измеряются с помощью вертикальной шкалы самого планшета и дополнительной миллиметровой линейки 4. В комплект также входят соединительные провода 5, и щуп 6 со скругленным концом. При выполнении работы одним из проводов 5 соединяет гнездо «*» (общую клемму) вольтметра с клеммой «минус» источника питания, другой провод используется для подключения щупа к вольтметру.

Рис.1. Состав лабораторной установки

 

Бумага, используемая в моделях, имеет значительное удельное сопротивление по сравнению с удельным сопротивлением медной фольги, из которой изготовлены электроды – «обкладки» модельных конденсаторов. Токи, текущие в бумаге, не сильно искажают распределение зарядов на электродах. Поэтому величина и направление вектора напряженности между электродами оказываются такими же, как в вакууме, а распределение потенциала в модели повторяет соответствующее распределение для оригинала. Подключая вольтметр с достаточно большим входным сопротивлением к одному из электродов и к произвольной точке бумаги, мы можем измерить разность потенциалов между этой точкой и электродом. Сопротивление вольтметра должно быть велико по сравнению с сопротивлением бумаги, для того чтобы измерительный ток вольтметра не шунтировал токи в модели и не искажал распределение электрического поля.

 

Теоретические основы лабораторной работы

Силовой характеристикой электрическогополя служит вектор его напряженности. Этот вектор в данной точке пространства определяетсясоотношением:

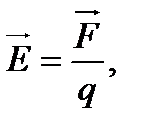
(1)

 

где 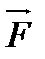- сила, действующая на неподвижный заряд 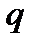, помещенный в данную точку.

Энергетической характеристикой электрического поля является его потенциал. Потенциалом в данной точке поля называется скалярная величина:

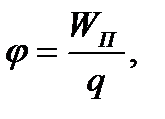
(2)

где 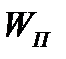– потенциальная энергия заряда 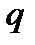, помещенного в данную точку. При перемещениизаряда 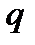из точки с потенциалом 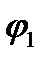в точку с потенциалом 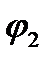силы электростатического полясовершают над зарядом работу:

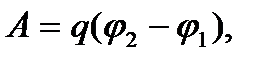
(3)

Геометрическое место точек, в которых потенциал имеет одинаковую величину, называетсяэквипотенциальной поверхностью.

Напряженность и потенциал электростатического поля связаны друг с другомсоотношениями:

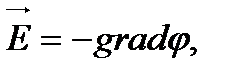
	(4)
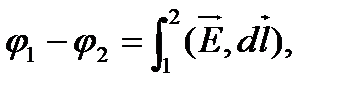
	(5)

Вектор градиента (градиент) потенциала в формуле (4) определяется через частныепроизводные потенциала по декартовым координатам :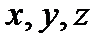

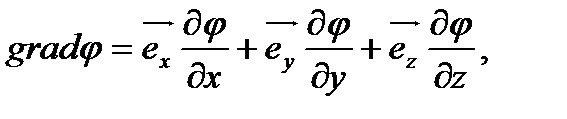
(6)

Здесь 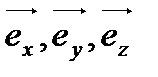– единичные вектора положительных направлений (орты) координатных осей 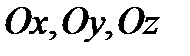. Направление градиента потенциала в данной точке совпадает с направлениембыстрейшего возрастания потенциала, а его величина равна быстроте изменения потенциала наединицу перемещения в этом направлении. Направление вектора 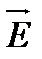напряженностиэлектростатического поля в соответствии с формулой (4) противоположно направлениюградиента. Следовательно, вектор напряженности направлен в сторонунаибыстрейшегоубывания потенциала. Кроме того, из формулы (5) следует, что вектор 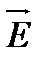перпендикулярен кэквипотенциальной поверхности в любой ее точке.

Если известны потенциалы 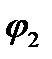и 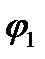двух точек, лежащих на одной силовой линии (рис.2), то средняя напряженность между этими точками вычисляется по формуле

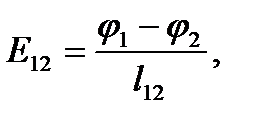
(7)

где 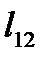– длина участка силовой линии между точками. Если относительное изменениелокального значения напряженности между выбранными точками невелико, то формула (7) даетзначение близкое к напряженности на середине участка 1-2.

 

Рис.2. АА’– эквипотенциальная поверхность с потенциалом 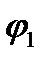,ВВ’– с потенциалом 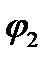; 1 и 2 – две точки одной силовойлинии

 

 

Внутри плоского конденсатора вдали от краев пластинэлектрическое поле однородно (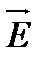 = const), и потенциал равномерно возрастает при движениивдоль координатной оси x от отрицательной обкладки к положительной (рис. 2а) по формуле

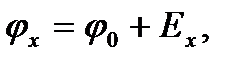
(8)

где 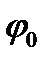–потенциал отрицательной пластины, 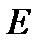–модуль вектора электрической напряженности.

 

Из формулы (7) следует, что:

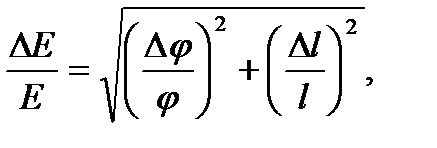
(9)

где 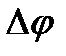и 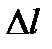- приборные погрешности.