2018-01-08
1830
6.2.1. Дифференциальное уравнение вынужденных электрических колебаний.
| L R C |
| U=U0sinωt ~ |
Пусть в электрический контур, содержащий последовательно соединенные индуктивность L, емкость С и резистор R, подается внешнее переменное напряжение U=U0cosωt, изменяющееся с циклической частотой ω (рис.1):
Рис.1
В любой момент времени для замкнутого контура должен выполняться второй закон Кирхгофа:
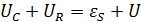(1)
Здесь UC – падение напряжения на конденсаторе, UR – падение напряжения на резисторе, εS – ЭДС самоиндукции и U – внешнее напряжение. Но:
; 
; 
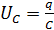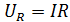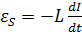
Следовательно, (1) можно представить в виде:
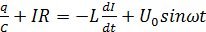(2)
Дифференцируя (2) по времени и учитывая, что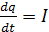 
, получим дифференциальное уравнение вынужденных электрических колебаний в последовательном электрическом контуре:
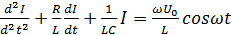(3)
Уравнение (3) есть неоднородное дифференциальное уравнение второго порядка относительно силы тока I.
Ясно, что вынужденные колебания тока имеют ту же частоту ω, что и внешнее напряжение. Поэтому решение уравнения (3) можно представить в виде:
|
|
|
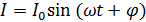, (4)
где I0 (амплитуда тока) и φ (начальная фаза) пока не известны.
6.2.2. Частные случаи решения дифференциального уравнения.
Для определения I0 и φ рассмотрим частные случаи решения (3) с привлечением векторной диаграммы тока и напряжений.
| U=U0sinωt ~ |
| R |
1. Электрическая цепь с резистором (рис.2).
Рис. 2
Дифференциальное уравнение (3) принимает вид:
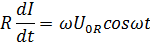
Разделяя переменные и выполняя операцию интегрирования, получим:
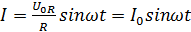(5)
где
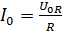– амплитуда тока
Сравнивая (5) с внешним напряжением U, приходим к выводу: колебания напряжения и силы тока в цепи с активным сопротивлением R проходят в одной фазе (напряжение и сила тока одновременно достигают своих минимальных и максимальных значений).
| L |
| U=U0sinωt ~ |
2. Электрическая цепь с индуктивностью L (рис.3).
Рис.3
Дифференциальное уравнение (3) принимает вид:
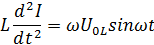
Интегрируя последнее выражение, получим
,
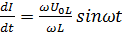или
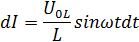
Выполняя повторное интегрирование, приходим к закону изменения силы тока во времени:
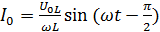, (6)
где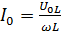 
– амплитуда тока.
Из (6) следует, что в цепи с индуктивностью L сила тока отстает в своем изменении во времени от напряжения на угол π/2.
| U=U0sinωt ~ |
| C |
3. Электрическая цепь с емкостью C (рис.4).
Рис. 4
Дифференциальное уравнение (3) принимает вид:
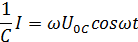
Откуда
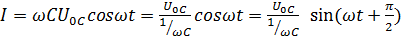, (7)
где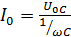 
– амплитуда тока.
Из (7) следует, что в цепи с емкостью C сила тока в своем изменении во времени опережает напряжение на угол π/2.
6.2.3. Векторная диаграмма тока и напряжений амплитудных значений. Закон Ома для цепи переменного тока.
Построим векторную диаграмму тока и напряжений для электрической цепи последовательно соединенных R, L, и C (рис.1)
|
|
|
За ось диаграммы примем ось тока (рис.5), на которой от начала диаграммы отложим амплитуду тока I0 (в последовательной цепи R, L, и C сила тока одна и та же для всех элементов).
| U0L (U0L- U0С) +π/2 φ –π/2 U0C |
| U0 I0 U0R ось токов |
Рис. 5
На активном сопротивлении R (резисторе) напряжение по фазе совпадает с током, а его амплитудное значение U0R=I0R отложим на оси тока.
На индуктивности напряжение опережает ток на π/2 (угол +π/2 отсчитывается против часовой стрелки), а амплитуда напряжения U0L=ωLI0
На емкости напряжение отстает от тока на π/2 (угол –π/2 отсчитывается по часовой стрелке), а амплитуда напряжения U0С=(1/ωС)I0 .
Как видно из рис.5 результирующее напряжение:
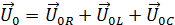
а его величина:
,
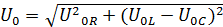или
,
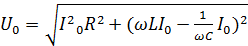откуда
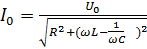(8)
Формула (8) есть закон Ома для цепи переменного тока. В отличие от закона Ома для постоянного тока, выражение (8) справедливо только для амплитудных значений силы тока и напряжения.
Отметим также, что ввиду инерционности электрические приборы фиксируют так называемые эффективные значения силы тока и напряжения, которые в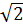 
раз меньше амплитудных, т.е. Iэф=I0/ 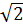и Uэф=U0/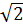
Следовательно (8) можно представить в виде:
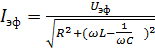(9)
Из векторной диаграммы (рис.5) следует, что в общем случае изменение напряжения не совпадает по фазе с изменением силы тока, так, что имеется сдвиг фаз (угол φ), величину которого можно рассчитать по формуле:
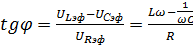(10)
6.2.4. Явление резонанса напряжений.
Как показывает (9), величина силы тока при заданных R, L, C существенно зависит от частоты ω переменного напряжения. Наибольшего значения сила тока достигает при
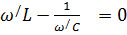(11)
где ω/ – значение частоты напряжения, при которой выполняется (11). Из (11) следует, что
,
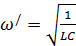что совпадает с собственной частотой ω0 колебаний электрического контура.
Итак, при
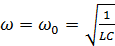(12)
амплитуда переменного тока (или эффективное значение силы тока) достигает максимального значения:
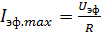(13)
При этом цепь последовательно соединенных R, L, C работает как чисто активное сопротивление.
Явление резкого возрастания силы тока в последовательной цепи переменного тока при совпадении частоты переменного напряжения ω с собственной частотой контура ω0 называется электрическим резонансом (точнее резонансом напряжений).
Величины XL=ωL и XС=1/ωС, входящие в формулы (8) и (9) носят названия соответственно индуктивного и емкостного сопротивлений. Иначе эти сопротивления называют реактивными. В отличие от активного (омического) сопротивления на реактивных сопротивлениях не происходит выделения ленц-джоулева тепла.
