Интегрирование в системе matlab. Численное интегрирование

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

(национальный исследовательский университет)»

ЧИСЛЕННЫЕ МЕТОДЫ В СРЕДЕ

КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ MATLAB

САМАРА 2012

Министерство образования и науки

Российской Федерации

 

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

(национальный исследовательский университет)»

 

 

ЧИСЛЕННЫЕ МЕТОДЫ В СРЕДЕ

КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ MATLAB

Методические указания к лабораторной работе

САМАРА2012

УДК 519.6

 

Составитель: А.А. Федотов

 

Численные методы в среде компьютерных вычисленийMATLAB: Метод. указания / – Самар. гос. аэрокосм. ун-т.; сост. А.А. Федотов; Самара, 2012. 16 с.

 

В методических указаниях изложены основные сведения об особенностяхреализации численных методов в среде компьютерных вычисленийMATLAB.Рассматриваются типовые примеры использования численных методовв среде MATLAB, таких как интерполяция функций, численное интегрирование и метод наименьших квадратов.Приведены порядок выполнения работы и требования к отчету.

Методические указания предназначены для студентов очно-заочной формы обучения, обучающихся по специальности 201000 «Биотехнические системы и технологии» и выполняющих лабораторные работы по дисциплине “Информационные технологии”. Подготовлены на кафедре радиотехники и медицинских диагностических систем.

Табл2. Ил. 2 Библиогр. 3 назв.

 

 

Печатаются по решению редакционно-издательского совета Самарского государственного аэрокосмического университетаимени академика С.П. Королева

 

Рецензент: И.А. Кудрявцев

 

 

 

Цель работы: изучить реализацию основных численных методов в среде компьютерных вычислений MATLAB.

 

Задачи:

1. Изучить синтаксис языка программирования MATLAB для решения задач численного интегрирования, интерполяции функций.

2. Используя полученные теоретические сведения, выполнить задания лабораторной работы и подготовить отчет.

 

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

 

Система компьютерных вычислений MATLABобладает большим набором встроенных функций, реализующих различные численные методы. К наиболее распространенным задачам математики, решаемыми численными методами относят нахождение корней трансцендентных уравнений, интегрирование, интерполирование, решение обыкновенных дифференциальных уравнений, решение задач линейной алгебры и ряд других.

 

Интерполирование

Интерполяция (интерполирование) – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. При выполнении научных или инженерных расчётов часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется получить аналитическую функцию, описывающую получаемые значения. Такая функция называется аппроксимирующей, а сам процесс построения такой функции называется аппроксимацией.

Основными видами интерполяции являются: точная в узлах и приближенная в узлах:

При интерполяции, точной в узлах, значения аппроксимирующей функции совпадают со значениями исходной функциив узлах интерполяции.

Рисунок 1 – Интерполяция точная в узлах

При интерполяции, приближенной в узлах, значения аппроксимирующей функции не совпадают со значениями исходной функции в узлах интерполяции.

Рисунок 2 – Интерполяция приближенная в узлах

(φ(x) – аппроксимирующая функция, Δ _i – отклонение значений аппроксимирующей функции от значения)

Интерполяция приближенная в узлах наиболее часто реализуется с помощью методов полиномиальной аппроксимация, коэффициенты полинома определяются с помощью метода наименьших квадратов. Суть метода наименьших квадратов заключается в подборе коэффициентов аппроксимирующей функции таким образом, чтобы сумма квадратов отклонений измеренных значений (ординаты экспериментальных точек) от расчетных значений (значения аппроксимирующей функции в узлах интерполяции) была наименьшей.

Для подбора коэффициентов полинома k-й степени методом наименьших квадратов в среде MATLAB есть функция polyfit, имеющая следующий синтаксис:

K=polyfit(x, y, n)

где: x – массив абсцисс экспериментальных точек (массив значений узлов интерполяции), y –массив ординат экспериментальных точек, n –степень полинома, K –массив коэффициентов полинома.

Для нахождения значения полинома в произвольной точке по известным коэффициентам полинома реализуется с помощью функции polyval:

Y=polyval(K, t)

где: K –массив коэффициентов полинома, t –абсцисса точки, в которой требуется вычислить значений полинома, данный параметр может быть также представлен массивом значений абсцисс, что позволяет получить массив значений полинома Y.

Для получения наилучших результатов интерполяции требуется подобрать оптимальное значение порядка аппроксимирующего полинома.

Для реализации метода интерполяции точной в узлах в среде MATLAB используется функция interp1, имеющая следующий синтаксис:

y _i =interp1(x, у, x _i, ‘method’)

где: x – массив абсцисс экспериментальных точек, y – массив ординат экспериментальных точек, x _i – массив значений аргументов, задаваемый пользователем, method – аргумент, позволяющий пользователю выбрать метод интерполяции, y _i – массив значений интерполирующей функции.

Методами интерполяции, применяемыми в функции interp1,являются:

• ' nearest '–ступенчатая (интерполяция по соседним точкам);

• ' linear ' – линейная;

• ' cubic ' – кубическая;

• ' spline ' – кубическими сплайнами.

В том случае, если параметр method функции interp1 не задан, то по умолчанию реализуется метод линейной интерполяции.

Самым простым способом интерполяции данных является ступенчатая интерполяция, при которой значение в каждой промежуточной точке принимается равным значению в ближайшей узловой точке.

Линейная интерполяция приводит к соединению соседних точек отрезками прямых, параметры которых подбираются оптимальным образом согласно соответствующим табличным данным.

Кубическая интерполяция аналогична линейной интерполяции, при этом соединение соседних точек осуществляется полиномами третьей степени.

Полиномиальная интерполяция зачастую не всегда обеспечивает удовлетворительные результаты интерполяции данных. Для обеспечения более качественной интерполяции данных используется метод аппроксимации сплайнами, обеспечивающий получение плавного перехода от одного значения к другому.

Сплайнпредставляет собой гладкую непрерывную функцию, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Существуют линейные, квадратичные и кубические сплайны.

Существенным недостатком сплайновой интерполяции является невозможность получения аналитической формы аппроксимирующей функции.

 

 

Интегрирование в системе MATLAB. Численное интегрирование

Система MATLAB позволяет вычислять неопределенные и определенные интегралы, первообразные которых заданы в виде аналитических выражений. Вычисление интегралов аналитическими методами осуществляется в системе MATLAB с помощью функций int, имеющей следующий синтаксис:

Int(f(x), а, b)

где: f(х) – подынтегральная функция; а, b – пределы интегрирования; необходимо указывать только при вычислении определенных интегралов.

С помощью функции int можно выполнять операции со следующими видами интегралов:

• неопределенный интеграл;

• неопределенный интеграл с символьными переменными;

• определенный интеграл с символьными значениями пределов интегрирования;

• определенный интеграл от алгебраических функций;

• кратные интегралы;

• несобственные интегралы.

Перед использованием символьных вычислений в среде MATLAB необходимо задать символьные переменные (то есть такие переменные, которым не присваивается числовое значений) с помощью команды syms:

Symsx, y, z

где: x, y, z – символьные переменные.

Для нахождения решения кратных интеграловнеобходимо произвести интегрированиерезультата, полученного от предыдущего значения интеграла.

При решении ряда математических задач часто встречаются интегралы с первообразной, которая не может быть выражена через элементарные функции (не существует аналитического решения), является слишком сложной, или задана в неявном виде, например, в табличной форме или в виде матрицы. В указанных случаях необходимо использовать методы численного интегрирования для решения соответствующих интегралов.

Под численным интегрированием понимают совокупность различныхчисленных методовнахождения значения определённого интеграла.Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую функцию, интеграл от которой легко вычисляется аналитически. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). Часто формулы для оценки значения интеграла называют квадратурными формулами.

Одним из наиболее распространенных методов реализации численного интегрирования является метод построения интегральных квадратурных формул для равномерных сеток, известный как формулы Котеса. Основной идеей метода является замена подынтегральной функции каким-либо интерполяционным многочленом. Вычисление определенного интеграла можно представить в виде:

где: числа H_i называются коэффициентами Котеса и вычисляются как интегралы от соответствующих многочленов, стоящих в исходном интерполяционном многочлене для подынтегральной функции при значении функции в узле

x_i=a+i∙h; h=(b−a)/N

h – шагсетки; N – числоузловсетки; i – индексузлов. Слагаемое r_N(f) определяет погрешность метода, которая может быть найдена разными способами. Для нечетных N ≥1 погрешность может быть найдена интегрированием погрешности интерполяционного полинома подынтегральной функции.Частными случаями формул Котеса являются: формулы прямоугольников (n=0), формулы трапеций (n=1), формула Симпсона (n=2), формула Ньютона-Котесаболее высоких порядков (n≥3).

В системе MATLAB вычисление интегралов реализовано численными методами трапеций, парабол (Симпсона) и метод Ньютона-Котеса.

Формула трапецийимеет следующий вид:

где: у₀ – значение подынтегральной функции при х = а; у_n – значение подынтегральной функции при х = b; h – шаг интегрирования.

Численное интегрирование в среде MATLAB на основе применения метода трапеций реализовано с помощью функций cumtrapz и trapz.

Функция cumtrapz выполняет интегрирование с накоплениемпо методу трапеций. Выходным параметром этой функции является вектор промежуточных вычислений, состоящий из N элементов, где N – число интервалов разбиения диапазона интегрирования функции. Значение последнего элемента вектора определяет итоговое значение интеграла.

Отличие функции trapz от функции cumtrapz состоит в том, что осуществляется простое интегрирование без накопления, то есть выходной параметр функции trapz представляет собой общее значение интеграла.

Функции trapz и cumtrapz имеют одинаковый синтаксис и имеют две формы записи:

Trapz(x, y)

В этом случае функция вычисляет интеграл, подынтегральная функция которого определена как y=f(x), при этом значения аргумента функции и значения самой функции задаются векторами.

Вторая форма записи функции имеет вид:

Trapz(y)

В данном случае подразумевается, что по умолчанию элементы вектора аргумента x принимают значения номеров элементов вектора значений функции y=f(x).

Основным недостатком метода трапеций является большая погрешность результата вычисления интеграла.

Формула парабол (Симпсона)имеет следующий вид:

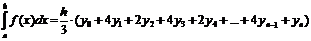
В этой формуле ординаты с нечетными индексами умножаются на 4, а с четными — на 2. В данном случае предполагается, что N — число четное, при нечетном N формула имеет вид:

Вычислительный алгоритм метода Симпсона с автоматическим выбором шага реализуется в среде MATLAB с помощью функции quad, имеющей следующий синтаксис:

quad(‘name’, a,b, tol, trace)

где: name – имя файл-функции, задающей подынтегральное выражение, а, b – пределы интегрирования; tol –опциональный параметр, задающий точность вычисления, по умолчанию равен 1.0e-06; trace –опциональный параметр, позволяющий получить информацию о ходе вычислений в виде таблицы, в столбцах которой представлены значение количества вычислений, начальная точка текущего промежутка интегрирования, его длина и значение интеграла; для задания этого параметра необходимо указать любое положительное число отличное от нуля.

В качестве параметра name можно использовать аналитическое выражение подынтегральной функции, взятое в одинарные кавычки.

Автоматический выбор шага интегрирования заключается в следующем: интервал интегрирования разбивают на n отрезков и вычисляют значение интеграла; если полученное значение не удовлетворяет заданной точности вычислений, то n увеличивают вдвое и вновь вычисляют значение интеграла, и так повторяют до тех пор, пока не будет достигнута заданная точность.

Функция quad8 реализует алгоритм численного интегрирования с помощью метода Ньютона-Котеса 8-го порядка.

Для вычисления двойного интеграла методомСимпсона используется функция dblquad, имеющая следующий синтаксис: