2018-01-08
252
Для представления операций над множествами удобно пользоваться диаграммами Эйлера-Венна.
1. Объединение множеств.
Результатом объединения множеств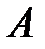 
и 
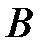будет являться множество 
такое, что любой элемент множества является элементом либо множества 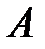, либо множества .
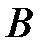Обозначение:
2. Пересечение множеств.
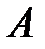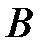Результатом пересечения множеств и будет являться множество такое, что любой элемент множества является одновременно и элементом множества 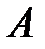, и элементом множества .
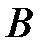Обозначение:
3. Разность множеств.
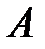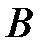Результатом разности множеств и будет являться множество такое, что любой элемент множества является элементом множества 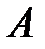, и не является элементом множества .
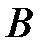Обозначение:
4. Дополнение множества.
Дополнением множества 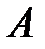до множества 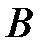будет являться множество такое, что любой элемент множества является элементом множества 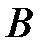, и не является элементом множества .
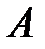Обозначение:
5. Симметрическая разность множеств.
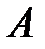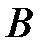Результатом симметрической разности множеств и будет являться множество такое, что любой элемент множества является элементом в точности одного множества 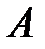или .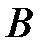
|
|
|
Обозначение:
Пример: Даны два множества 
и 
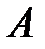. Выполнить операции объединения множеств, пересечения множеств, разности множеств, дополнения множества до 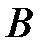, симметрической разности множеств.
Решение:
Пример: Из 100 студентов 28 изучают английский язык, 30 – немецкий, 42 – французский, 8 – английский и немецкий, 10 – английский и французский, 5 – немецкий и французский, 3 – немецкий, английский и французский. Сколько студентов изучают французский язык?
Решение: Решение данной задачи легко получить с помощью диаграмм Эйлера-Венна.
Пример: Доказать, что если 
и 
, то 
.
Доказательство: Из определения пересечения и объединения следует, что множества 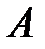и 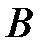состоят из одних и тех же элементов, т.е. .
Пример: Доказать, что 
.
Доказательство:
Пример: Верно ли, что для произвольных множеств 
и 
верно равенство 
?
Решение:
Выберем 2 элемента 
и 
некоторого множества и запишем их в следующем виде: 
. Если строго определить первый и второй элементы пары, то полученную пару назовем упорядоченной, где - первый элемент пары, - второй элемент пары.
- упорядоченная пара,
- упорядоченная тройка,
…
Обобщением понятия упорядоченной пары является упорядоченная n-ка или кортеж 
. Простейшим примером кортежа является вектор.
Упорядоченные пары называются равными и записываются 
, если только выполнено условие: 
и 
. В частности, 
, если 
.
Декартовым (прямым) произведение множеств 
называется множество упорядоченных n-ок (множество кортежей) 
, где 
, 
, …, 
, и обозначают 
. Таким образом,
|
|
|
Пример: Даны множества 
, 
. Найти 
, 
, 
.
Решение:
Пример: Даны множества 
, 
и 
. Найти 
.
Решение:
