Определения
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,  ,
, 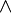 ,
, 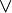 , 0, 1}, где B— непустое множество, над элементами которого определены три операции:
, 0, 1}, где B— непустое множество, над элементами которого определены три операции:
 отрицание (унарная операция),
отрицание (унарная операция),
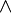 конъюнкция (бинарная),
конъюнкция (бинарная),
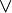 дизъюнкция (бинарная),
дизъюнкция (бинарная),
а такжеконстанты— логический ноль 0 и логическая единица 1.
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = {Ложь, Истина}
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь на этот математический инструментарий,логика высказыванийизучаетвысказыванияипредикаты. Также вводятся дополнительные операции, такие какэквиваленция 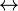 («тогда и только тогда, когда»),импликация
(«тогда и только тогда, когда»),импликация 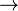 («следовательно»), сложение по модулю два
(«следовательно»), сложение по модулю два 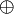 («исключающее или»),штрих Шеффера
(«исключающее или»),штрих Шеффера 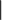 ,стрелка Пирса
,стрелка Пирса 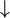 и другие.
и другие.
Рассмотрим логические операции над высказываниями.
Отрицание. Отрицанием высказывания А называется новое высказывание, которое является истинным, если высказывание А ложно, и ложным, если высказывание А истинно. Обозначается отрицание 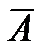 илиØ А и читается “не А ” или “неверно, что А ”. Логические значения высказываний
илиØ А и читается “не А ” или “неверно, что А ”. Логические значения высказываний 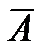 можно описать с помощью таблицы истинности, где 0 означает ложь, а 1 – истину. Таблица истинности для отрицания имеет вид:
можно описать с помощью таблицы истинности, где 0 означает ложь, а 1 – истину. Таблица истинности для отрицания имеет вид:
|
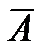 также является высказыванием, следовательно можно образовать отрицание и от
также является высказыванием, следовательно можно образовать отрицание и от 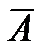 , которое называется двойным отрицанием высказывания А. Ясно, что двойное отрицание высказывания А совпадает с самим высказыванием А.
, которое называется двойным отрицанием высказывания А. Ясно, что двойное отрицание высказывания А совпадает с самим высказыванием А. | A | B | AB |
Конъюнкция (логическое умножение).Конъюнкцией двух высказываний А, В называется новое высказывание, которое считается истинным, если оба высказывания А, В истины, и ложным, если хотя бы одно из них ложно. Обозначается конъюнкция по-разному. Например, А ´ B, AB, А Ù В, А & B, А × B, читается “ А и В ”. Логические значения конъюнкции описываются следующей таблицей истинности:
|
Импликация. Импликацией двух высказываний A, B называется новое высказывание, которое считается ложным, если A истинно, а B - ложно, и истинным во всех остальных случаях.
|
Логические значения операции импликации описываются следующей таблицей истинности:
Употребление грамматической связки «если..., то...» в математической логике отличается от употребления их в обычной речи, где мы, как правило, считаем, что если высказывание A ложно, то высказывание «Если A, то B» вообще не имеет смысла. Кроме того, строя предложение вида «если A, то B» в обыкновенной речи, мы всегда подразумеваем, что предложение B вытекает из предложения A.
Употребление грамматической связки «если..., то...» в математической логике не требует этого, поскольку в математической логике смысл высказываний не рассматривается, а рассматривается лишь их логическое значение.
Эквиваленция. Эквиваленцией (или эквивалентностью) двух высказываний А, В называется новое высказывание, которое считается истинным, когда оба высказывания А, В либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний А, В обозначается символом А «В, читается «для того, чтобы В, необходимо и достаточно, чтобы А», или «А тогда и только тогда, когда В». Логические значения операции эквиваленции описываются следующей таблицей истинности:
|
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем математики формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух элементов эквивалентности и доказав истинности самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Пример. Пусть А - высказывание «Вася изучает программирование», В - высказывание «Васялюбит математику». Рассмотрим словесную формулировку высказываний: 1) А Ú В; 2) 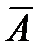 &
& 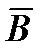 ; 3) A ® B; 4)
; 3) A ® B; 4) 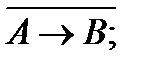 5)
5) 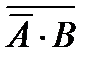 ; 6)
; 6) 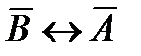 .
.
Решение:
1) «Васяизучает программирование или любит математику».
2) «Васяне изучает программирование и не любит математику».
3) «Если Васяизучает программирование, то он любит математику».
4) «Неверно, что если Васяизучает программирование, то он любит математику».
Остальные задания предлагается читателю записать самостоятельно.
Формулы алгебры логики. С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками или операции выполняются согласно определенному приоритету.
Например, из трех высказываний А, В, С можно построить высказывания  и
и 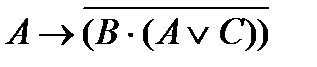 . Всякое простое высказывание и всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения конечного числа логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики.
. Всякое простое высказывание и всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения конечного числа логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются, т.е. при выполнении операций алгебры логики соблюдаются следующие приоритеты:
1. Выполнениеопераций в скобках
2. Операциялогическогоотрицания.
3. Операциялогическогоумножения
4. Операциялогическогосложения.
5. Операцияимпликации.
6. Операцияэквивалентности.
Операции с равным приоритетом выполняются слева направо.
В связи с этим формулы 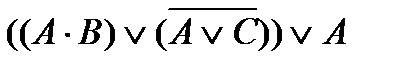 могут быть записаны так: А×В Ú
могут быть записаны так: А×В Ú 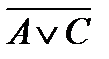 Ú А, а формула
Ú А, а формула 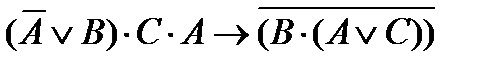 в виде
в виде 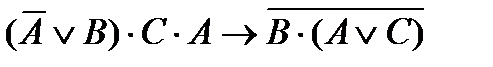 .
.
Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в нее элементарных высказываний. Все возможные логические значения формулы, в зависимости от значений входящих в нее элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности. Например, дляформулы 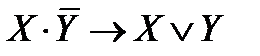 таблицаистинностиимеетвид:
таблицаистинностиимеетвид:
| X | Y | 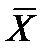 | 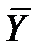 | 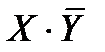 |  | 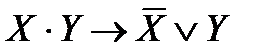 |
Легко видеть, что если формула содержит n элементарных высказываний, то она принимает 2 n значений, состоящих из нулей и единиц, или, что то же, ее таблица истинности содержит 2 n строк. Так, для формулы, содержащей три переменные, таблица истинности будет иметь 23 = 8 строк, и формула принимает 8 значений, состоящих из нулей и единиц. Например, дляформулы 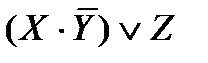 таблицаистинностиимеетвид:
таблицаистинностиимеетвид:
| X | Y | Z | 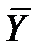 | 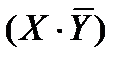 | 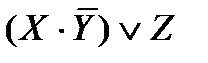 |
 2018-01-08
2018-01-08 1114
1114
