Тригонометрические выражения

Разобьем интегралы от тригонометрических выражений на несколько групп.

I. - это означает, что над синусом и косинусом проведены только рациональные операции (+, –, ^.,:, ^). Интегралы такого типа сводятся к интегралам от рациональных дробей путем универсальной тригонометрической подстановки:

tg(x/2)=t.

Выразим x и получим dx: .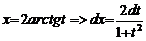

Подготовим выражения через t для sin x и cos x:

=>

=>

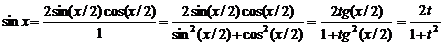Пример 17.

Частные случаи, когда универсальная тригонометрическая подстановка не эффективна, поскольку приводит к громоздким выкладкам:

1) – подынтегральная функция нечетная относительно синуса. Рекомендуемая подстановка: cos x = t.

2) – подынтегральная функция нечетная относительно косинуса. Рекомендуемая подстановка: sin x = t.

3) – подынтегральная функция четная относительно синуса и косинуса. Рекомендуемая подстановка:

Пример 18.

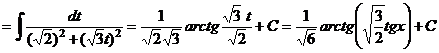
II. Интегралы вида

а) n – четное. Интеграл сводится к табличным методом понижения степени:

Пример 19.

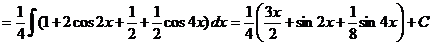
б) n – нечетное. Интеграл сводится к табличным методом отделения одной нечетной степени.

Пример 20.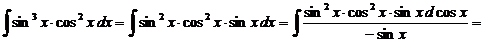

III. Интегралы вида

а) Рекомендуемая подстановка:

б) ИЛИ Применить формулы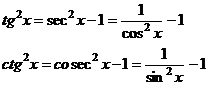

Пример 21.

IV. Интегралы вида

Интегралы сводятся к табличным при использовании тригонометрических формул: ;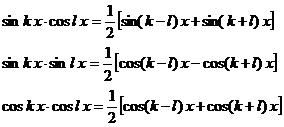

V. Интегралы вида , где p и r – рациональные числа, причем (p + r) – четное отрицательное число. Рекомендуемая подстановка:

Пример 22.