Иррациональные (также как и трансцендентные) выражения интегрируются в элементарных функциях только в некоторых определенных случаях. Все эти приемы можно назвать методами рационализации подынтегрального выражения.
1)  Простейшие выражения подынтегральной функции, содержащей квадратный трехчлен. Этот вариант иррациональности был рассмотрен в примере 8.
Простейшие выражения подынтегральной функции, содержащей квадратный трехчлен. Этот вариант иррациональности был рассмотрен в примере 8.
Пример 23. 


 .
.
Если кроме квадратного трехчлена присутствуют еще какие-либо множители, принцип решения интеграла остается прежним.
Пример 24. 



 .
.
2)  Рекомендуемая подстановка:
Рекомендуемая подстановка: 
 Рекомендуемая подстановка:
Рекомендуемая подстановка: 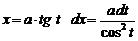
 Рекомендуемая подстановка:
Рекомендуемая подстановка: 
Пример 25. 





Пример 26. 
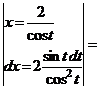


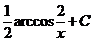
3)  , где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой:
, где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой:  , где s – наименьшее общее кратное a, b, g …
, где s – наименьшее общее кратное a, b, g …
Пример 27. 



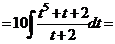 выделяем целую часть
выделяем целую часть 


4) 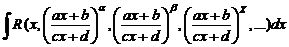 , где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой:
, где a, b, g …– дробные рациональные числа. Рационализация проводится подстановкой:  , где s – наименьшее общее кратное a, b, g
, где s – наименьшее общее кратное a, b, g
Пример 28. 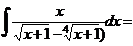
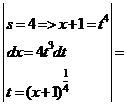



5) Интегрирование дифференциальных биномов.
ОПР. 6 Выражение вида  где (m,n,p,a,b) – const, называется дифференциальным биномом.
где (m,n,p,a,b) – const, называется дифференциальным биномом.
Теорема 5. ( Чебышева )
Интегралы  (m,n,p ∈ Q) выражаются в конечном виде через элементарные функции, если оказывается целым одно из чисел:
(m,n,p ∈ Q) выражаются в конечном виде через элементарные функции, если оказывается целым одно из чисел:
1) p (подстановка  , где s – наименьшее общее кратное m и n)
, где s – наименьшее общее кратное m и n)
2)  (подстановка
(подстановка 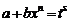 , где s – знаменатель p)
, где s – знаменатель p)
3)  (подстановка
(подстановка  , где s – знаменатель p)
, где s – знаменатель p)
Пример 29. 



Пример 30.
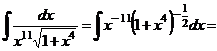
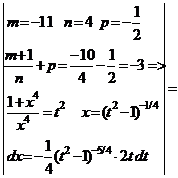



 2018-01-08
2018-01-08 1351
1351








