ТЕОРЕМА 2.
Пусть требуется найти  , где первообразная не табличная.
, где первообразная не табличная.
Пусть 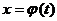 ,
,  – непрерывная функция с непрерывной производной, имеющая обратную функцию.
– непрерывная функция с непрерывной производной, имеющая обратную функцию.
Тогда 

Доказательство.
Докажем, что производные левой и правой части равны.
Левая: 
Правая:  как сложную функцию от t
как сложную функцию от t 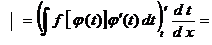

 ч.т.д.
ч.т.д.
Однако одного общего правила для выбора подстановки не существует.
Рекомендуемые подстановки
1. Если подынтегральное выражение содержит функцию и ее производную:

Подстановка:  ,
, 


 .
.
Таким образом, можно сформулировать правило: если подынтегральное выражение содержит функцию и ее производную, то под дифференциал надо подставить функцию и разделить на ее производную.
Пример 3. 
Такая подстановка называется подведение под знак дифференциала.
Пример 4.  =
= 
Пример 5. 

2. Если подынтегральное выражение содержит функцию в дробной степени, бывает удобно выполнить замену переменных.
Пример 6. 



3. Интегрирование квадратных трехчленов  и
и  . Для интегрирования квадратных трехчленов в знаменателе используется прием выделения полного квадрата и замены полного квадрата на новую переменную
. Для интегрирования квадратных трехчленов в знаменателе используется прием выделения полного квадрата и замены полного квадрата на новую переменную
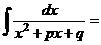

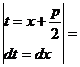

 .
.




 .
.
Пример 7. 



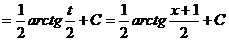
Пример 8. 



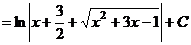 .
.
Интегрирование по частям
Теорема 3. Пусть U(x) и V(x) две дифференцируемые функции.
Тогда 
 .
.
Доказательство: По свойству дифференциала произведения имеем

Проинтегрируем обе части равенства


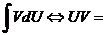



 ч.т.д.
ч.т.д.
Применять интегрирование по частям целесообразно, если интеграл  проще, чем
проще, чем 
Удобно все интегралы, которые следует брать по частям, разбить на 3 группы.
1. 2 3








U d V U d V U d V
или V d U
где  - полином степени n.
- полином степени n.
Пример 9.  . Интеграл относится ко 2-ой группе, => за U возьмемln2 x.
. Интеграл относится ко 2-ой группе, => за U возьмемln2 x. 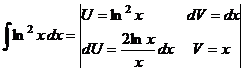



Третья группа интегралов называется циклические – после нескольких шагов применения теоремы интегрирования по частям, мы должны прийти к исходному интегралу. Для этой группы в качестве U можно выбрать любой множитель.
Пример 10. 

 .
.
Таким образом, мы получили 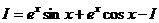 . Выражаем отсюда
. Выражаем отсюда  и получаем
и получаем  .
.
С помощью интегрирования по частям можно получать рекуррентные формулы для вычисления интегралов  .
.
Пример 11. (Важный!)





 , где
, где  ,
,  . =>
. =>
 . Т.о.
. Т.о.  . Или
. Или
 . Далее, понижая степень n до первой, приходим к табличному интегралу.
. Далее, понижая степень n до первой, приходим к табличному интегралу.
Интегрирование рациональных дробей.
В общем случае интегрирование не имеет заранее предусмотренных правил, но именно в случае рациональных выражений интегрирование представляет собой определенный порядок действий. Вспомним из школьного курса алгебры свойства целой рациональной функции.
В параграфе «формула Тейлора» мы определили полином, как функцию целых степеней x. Перепишем полином (многочлен) в другом порядке и будем называть его целой рациональной функцией 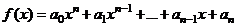 ,
,  .
.
Повторимся: два многочлена f(x) и g(x) считаются равными, если равны коэффициенты ai=bi при равных степенях x.
ОПР. 3 Рациональной дробью (дробно-рациональной функцией) называется частное от деления двух целых рациональных функций
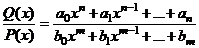
Дробь  называется правильной, если n < m (степень Q(x) меньше степени P(x)). Если n > m, дробь
называется правильной, если n < m (степень Q(x) меньше степени P(x)). Если n > m, дробь  – неправильная. Тогда ее можно представить в виде суммы многочлена n –m и правильной дроби, поделив числитель на знаменатель столбиком (выделить целую часть).
– неправильная. Тогда ее можно представить в виде суммы многочлена n –m и правильной дроби, поделив числитель на знаменатель столбиком (выделить целую часть).
Основная теорема алгебры. Всякая целая рациональная функция имеет по крайней мере один корень (действительный или мнимый).
Теорема. Всякий многочлен n -ой степени разлагается на n линейных множителей и множитель – константу, который равен коэффициенту при xn.
Теорема. Многочлен Pn не может иметь более чем n различных корней. Если некоторые повторяются, то их можно объединить, и говорят, что x=xi – корень кратности k1.
Теорема. Если среди корней есть мнимые, то они обязательно сопряженные и множитель, за счет которого образуются мнимые корни, можно оставлять в виде квадратного трехчлена x 2 +px+q – многочлен 2-ой степени.
Таким образом, для любого P(x) можно записать:

ОПР. 5 Простейшими (элементарными) дробями называются дроби следующего вида:
1.  2.
2.  3.
3.  4.
4. 
Теорема 4. Всякая правильная рациональная дробь  может быть представлена и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением на множители знаменателя P(x).
может быть представлена и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением на множители знаменателя P(x).



где  – неопределенные коэффициенты – константы.
– неопределенные коэффициенты – константы.
Примеры разложения дробей на простейшие.
Пример 12. Разложить дробь 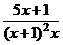 на сумму простейших дробей и вычислить коэффициенты.
на сумму простейших дробей и вычислить коэффициенты.
 . Определим значения коэффициентов А, В, С. Для этого приведем к общему знаменателю правую часть равенства.
. Определим значения коэффициентов А, В, С. Для этого приведем к общему знаменателю правую часть равенства.
 . Знаменатели первой и последней дроби одинаковы, следовательно, чтобы выполнялось равенство, числители также должны быть равны:
. Знаменатели первой и последней дроби одинаковы, следовательно, чтобы выполнялось равенство, числители также должны быть равны:  . По опр.3 два многочлена равны, если равны коэффициенты при одинаковых степенях x. => Приравняем коэффициенты при равных степенях x левой и правой частей равенства:
. По опр.3 два многочлена равны, если равны коэффициенты при одинаковых степенях x. => Приравняем коэффициенты при равных степенях x левой и правой частей равенства:
 =>
=>  .
.
Пример 13. Разложить дробь  на сумму простейших дробей.
на сумму простейших дробей.  .
.
Пример 14. Разложить дробь 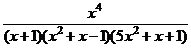 на сумму простейших дробей.
на сумму простейших дробей.
Числитель – многочлен степени 4, знаменатель – многочлен степени 5. => Дробь правильная. 
или  =>
=>

Прежде чем приступить к интегрированию рациональных выражений, рассмотрим интегралы от простейших дробей.
1.  .
.
2. 
3.  интеграл берется тем же способом, что и в примере 7.
интеграл берется тем же способом, что и в примере 7.




 .
.
4.  замена аналогична
замена аналогична  (первый интеграл элементарный, второй берется по рекуррентной формуле пример 11)
(первый интеграл элементарный, второй берется по рекуррентной формуле пример 11)  , где
, где  .
.
Порядок действий при вычислении интеграла от рационального выражения.
1. Выделить целую часть (сделать дробь  правильной).
правильной).
2. Разложить знаменатель на множители.
3. Записать дробь в виде суммы простейших дробей.
4. Определить коэффициенты.
5. Проинтегрировать.
Пример 15.  .
.
1. Рассмотрим подынтегральную функцию  – неправильная дробь. Выделим целую часть.
– неправильная дробь. Выделим целую часть.
 – делением многочлена на многочлен получили 2 x – целую часть и остаток 1. =>
– делением многочлена на многочлен получили 2 x – целую часть и остаток 1. => 
 .
.
2-3. Разложим знаменатель на множители и запишем в виде суммы простейших дробей: 
4. Определим коэффициенты:  =>
=>  =>
=>  =>
=> 
5. Проинтегрируем 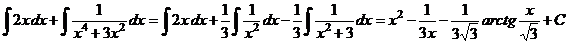 .
.
Пример 16. Доказать, что 
Рассмотрим подынтегральное выражение  – правильная дробь.
– правильная дробь.
 =>
=> 
Если корни простые – коэффициенты найдутся быстрее, если удобно выбрать значения x.
 . =>
. => 
 2018-01-08
2018-01-08 1428
1428