Исследование функций с помощью производных

Лекция 26. Исследование поведения функций с помощью первой и второй производной, асимптоты. Построение графиков функций.

Исследование функций с помощью производных

Теорема1. Если функция 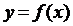возрастает на некотором интервале 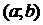оси ох (с ростом x растет и y) и дифференцируема на этом интервале, то для любого x из этого интервала 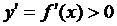(производная имеет знак (+)). А если она убывает на этом интервале (y убывает с ростом x) и дифференцируема на нем, то для любого x из этого интервала 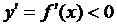(производная имеет знак (–)).

Доказательство.

Рассмотрим сначала рис.1. На нем изображен график возрастающей и дифференцируемой на интервале 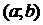функции 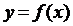. В каждой точке M этого графика касательная составляет с осью ох острый угол 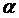(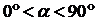). Но тангенсы острых углов, как известно, положительны. Значит, согласно геометрического смысла производной, производная 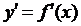положительна для любых x из интервала 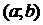возрастания функции.

А теперь рассмотрим рис. 2, на котором изображен график убывающей на интервале 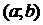функции 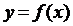. Здесь для любой точки М графика функции (а значит, для любого x из интервала 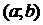) угол 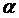наклона касательной, проведенной к графику функции, тупой (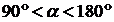). Но тангенсы таких углов отрицательны. А значит и производная 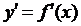отрицательна.

Следствие теоремы 1. Если на некотором интервале 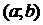оси ох в любой его точке x производная функции 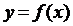положительна, то функция возрастает на этом интервале. А если отрицательна – то убывает. Это следствие играет очень важную роль в исследовании функций. Оно позволяет по знаку производной функции определять, растет или убывает функция, и где именно (для каких x) растет, и где (для каких x) убывает.

Докажем более строгий вариант теоремы 1.

Теорема 2. 1). Если функция 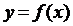, имеющая производную на отрезке 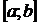, возрастает на этом отрезке, то ее производная на отрезке 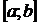не отрицательна, т.е. .

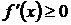2) Если функция 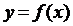непрерывна на отрезке 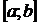и дифференцируема в промежутке 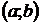, причем 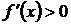для 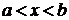, то эта функция возрастает на отрезке .

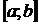Доказательство. 1) Пусть y=f(x) возрастает на отрезке 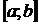. Придадим аргументу х приращение 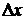и рассмотрим отношение

. (*)

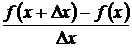Так как f(x) – функция возрастающая, то

В обоих случаях 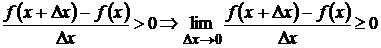по свойствам пределов функций. Т.е. 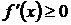, что и требовалось доказать.

2) Пусть 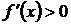при всех значениях х, принадлежащих промежутку 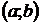. Рассмотрим два любых значения x₁ и x₂, x₁ < x₂, принадлежащих отрезку 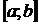. По теореме Лагранжа о конечных приращениях имеем:

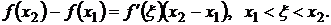
По условию 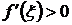, следовательно 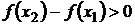, а это означает, что f(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающей дифференцируемой функции.

Теорема 3. 1). Если функция 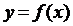, имеющая производную на отрезке 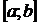, убывает на этом отрезке, то ее производная на отрезке 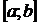не положительна, т.е. .

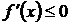2) Если функция 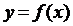непрерывна на отрезке 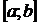и дифференцируема в промежутке 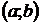, причем 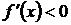для 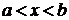, то эта функция убывает на отрезке .

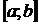Пример 1. Рассмотрим функцию 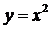. Ее производная 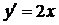. Она положительна при 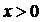и отрицательна при 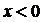. Значит, при 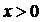функция 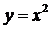возрастает, а при 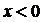она убывает. График этой функции (парабола) наглядно подтверждает сказанное.