2018-01-08
570
Любое эконометрическое исследование обычно начинают с предположения о линейной взаимосвязи между исследуемыми показателями, т.е. строят уравнение линейной регрессии:
.
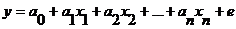Построение (параметризация) линейного регрессионного уравнения состоит в оценке его неизвестных коэффициентов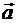 
. Классический подход к оцениванию коэффициентов уравнения регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки коэффициентов 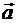= (a 0, a 1 ,..., an), при которых сумма квадратов отклонений фактических (наблюдаемых) значений зависимой переменной y от тех значений 
этой переменной, которые можно рассчитать по построенному уравнению регрессии, является наименьшей:
,
где 
и 
- фактические данные; 
, 
,…, 
- оценки коэффициентов линейного уравнения регрессии;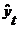 
- расчетные значения зависимой переменной; N - число наблюдений; 
- оценки значений случайной ошибки, называемые остатками.
Значения коэффициентов , ,…, 
, при которых функция G имеет минимум, называют оценками метода наименьших квадратов. Их можно найти, решив систему нормальных уравнений вида:
.
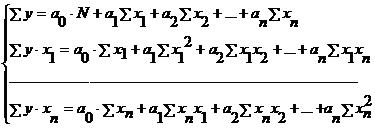Решения такой системы можно осуществить методом определителей:
, 
, 
, …, 
,
где 
- определитель системы, 
и 
,…, 
- частные определители, получаемые путем замены соответствующего столбца определителя системы данными из левой части системы уравнений :
; 
и т. д.
Рассчитанные значения , ,…, коэффициентов уравнения регрессииназываются их МНК – оценками.
Результатом выполнения этапа параметризации является уравнение регрессии,называемое моделью прогноза:
.
