Обобщением системы Цезаря является аффинная криптосистема. Она определяется двум числами a и b, где 0<=a, b<=n-1. n - как и раньше, является мощностью алфавита. Числа a и n должны быть взаимно просты.
Соответствующими заменами являются:
Aa,b(j)=(a*j+b)(mod n) (1.4)
A-1a,b(j)=(j-b)*a-1(mod n) (1.5)
Обратную замену также можно получить, просто поменяв местами строки в таблице замен.
Взаимная простота a и n необходима для биективности отображения, в противном случае возможны отображения различных символов в один и неоднозначность дешифрирования.
Шифр Полибия
Система Цезаря не является старейшей. Возможно, что наиболее древней из известных является система греческого историка Полибия, умершего за 30 лет до рождения Цезаря. Его суть состоит в следующем: рассмотрим прямоугольник, часто называемый доской Полибия.
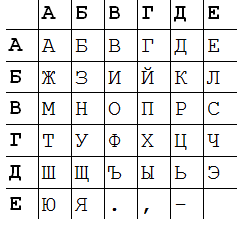
Каждая буква может быть представлена парой букв, указывающих строку и столбец, в которых расположена данная буква. Так представления букв В, Г, П, У будут АВ, АГ, ВГ, ГБ соответственно.
Методы вскрытия одноалфавитных систем
|
|
|
При своей простоте в реализации одноалфавитные системы легко уязвимы. Определим количество различных систем в аффинной системе. Каждый ключ полностью определен парой целых чисел a и b, задающих отображение ax+b. Для а существует j(n) возможных значений, где j(n) - функция Эйлера, возвращающая количество взаимно простых чисел с n, и n значений для b, которые могут быть использованы независимо от a, за исключением тождественного отображения (a=1 b=0), которое мы рассматривать не будем. Таким образом получается j(n)*n-1 возможных значений, что не так уж и много: при n=33 в качестве a могут быть 20 значений(1, 2, 4, 5, 7, 8, 10, 13, 14, 16, 17, 19, 20, 23, 25, 26, 28, 29, 31, 32), тогда общее число ключей равно 20*33-1=659. Перебор такого количества ключей не составит труда при использовании компьютера. Но существуют методы упрощающие этот поиск и которые могут быть использованы при анализе более сложных шифров.
Частотный анализ
Одним из таких методов является частотный анализ. Распределение букв в криптотексте сравнивается с распределением букв в алфавите исходного сообщения. Буквы с наибольшей частотой в криптотексте заменяются на букву с наибольшей частотой из алфавита. Вероятность успешного вскрытия повышается с увеличением длины криптотекста. Существуют множество различных таблиц о распределении букв в том или ином языке, но ни одна из них не содержит окончательной информации - даже порядок букв может отличаться в различных таблицах. Распределение букв очень сильно зависит от типа теста: проза, разговорный язык, технический язык и т.п. В методических указаниях к лабораторной работе приведены частотные характеристики для различных языков, из которых ясно, что буквы буквы I, N, S, E, A (И, Н, С, Е, А) появляются в высокочастотном классе каждого языка.
|
|
|
Простейшая защита против атак, основанных на подсчете частот, обеспечивается в системе омофонов (HOMOPHONES) - однозвучных подстановочных шифров, в которых один символ открытого текста отображается на несколько символов шифротекста, их число пропорционально частоте появления буквы. Шифруя букву исходного сообщения, мы выбираем случайно одну из ее замен. Следовательно простой подсчет частот ничего не дает криптоаналитику. Однако доступна информация о распределении пар и троек букв в различных естественных языках. Криптоанализ, основанный на такой информации будет более успешным.
Метод полосок
Для шифра Цезаря имеется более простой способ расшифровки - так называемый метод полосок. На каждую полоску наносятся по порядку все буквы алфавита. В криптограмме берется некоторое слово. Полоски прикладываются друг к другу так, чтобы образовать данное слово. Двигаясь вдоль полосок находится осмысленное словосочетание, которое и служит расшифровкой данного слова, одновременно находится и величина сдвига (Рис. 1.1).

Рисунок 1.1. – Метод полосок.
 2018-01-08
2018-01-08 3057
3057








