Эластичность функции и ее геометрический смысл

Пусть величина y зависит от x, и эта зависимость описывается функцией . Изменение независимой переменной приводит в силу функциональной зависимости к изменению переменной . Одним из показателей реагирования одной переменой на изменение другой служит производная

В экономике этот показатель неудобен тем, что он зависит от выбора единиц.

Поэтому для измерения чувствительности изменения функции к изменению аргумента в экономике изучают связь на абсолютных изменений переменных x и y и , а их относительных или процентных изменений.

Эластичностью функции называется передел отношения относительных изменений переменных y и x.

Если эластичность обозначить E_x(y), то

Где - маржинальное значение функции в точке x, 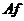- среднее значение функции в точке x. Эту эластичность называют также предельной или точечной эластичностью (в виде отношения предельной и средней величин).

Можно работать с“логарифмической производной”

Геометрически эластичность убывающей функции равна отношению расстояний по касательной от точки C с координатами 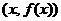до ее пересечения с осями Y и X, взятому, соответственно, со знаком “-“.

Дискретный случай.

В дискретном случае, а так же при приближенном определении эластичности по дискретному набору данных различают:

конечную (процентную) эластичность

Среднюю (дуговую) эластичность