Определение 4.2. Число 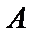 называется пределом функции
называется пределом функции 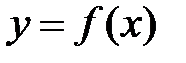 при
при 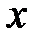 , стремящемся к бесконечности, если для любого положительного числа
, стремящемся к бесконечности, если для любого положительного числа 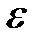 найдется такое положительное число
найдется такое положительное число 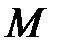 , что для всех
, что для всех 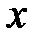 , удовлетворяющих условию
, удовлетворяющих условию 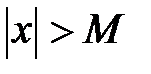 , выполняется неравенство
, выполняется неравенство 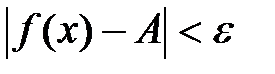 . Символически это записывается так:
. Символически это записывается так: 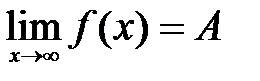 . Если
. Если 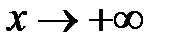 , то пишут
, то пишут 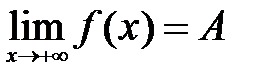 , если
, если 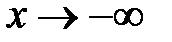 , то –
, то – 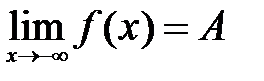 .
.
Коротко определение предела функции на бесконечности можно записать следующим образом:
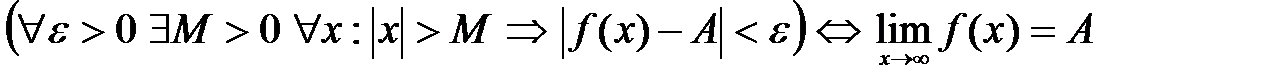 .
.
Бесконечно малые и бесконечно большие функции.
Определение 4.3. Если предел 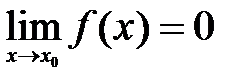 , то функция
, то функция 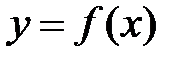 называется бесконечно малойпри
называется бесконечно малойпри 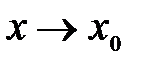 . Если предел
. Если предел 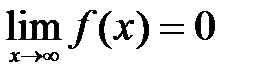 , то функция
, то функция 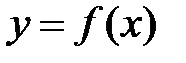 называется бесконечно малойпри
называется бесконечно малойпри 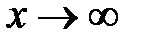 .
.
Пример 4.2. Примеры бесконечно малых функций:
а) 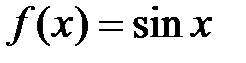 при
при 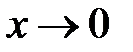 ; б)
; б) 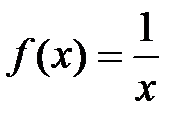 при
при 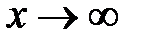 ; в)
; в) 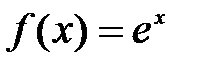 при
при 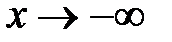 .
.
Определение 4.4. Функция 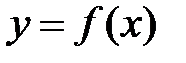 называется бесконечно большой при
называется бесконечно большой при 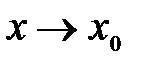 , если для любого положительного числа
, если для любого положительного числа 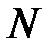 найдется такое положительное число
найдется такое положительное число 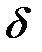 , что для всех
, что для всех 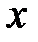 , удовлетворяющих условию
, удовлетворяющих условию 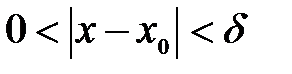 , выполняется неравенство
, выполняется неравенство 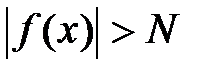 . Обозначают так:
. Обозначают так: 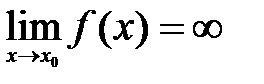 , причем если
, причем если 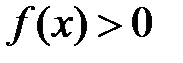 , то
, то 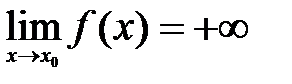 , если
, если 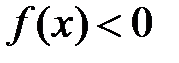 , то
, то 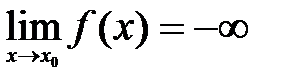 .
.
Коротко это определение можно записать так:
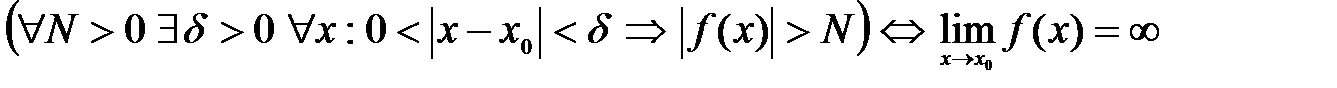 .
.
Определение 4.5. Функция 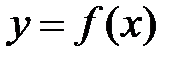 называется бесконечно большой при
называется бесконечно большой при 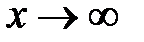 , если для любого положительного числа
, если для любого положительного числа 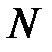 найдется такое положительное число
найдется такое положительное число 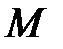 , что для всех
, что для всех 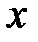 , удовлетворяющих условию
, удовлетворяющих условию 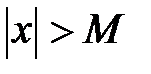 , выполняется неравенство
, выполняется неравенство 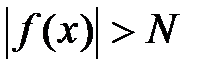 . Обозначают так:
. Обозначают так: 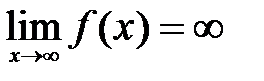 .
.
Коротко это определение можно записать так:
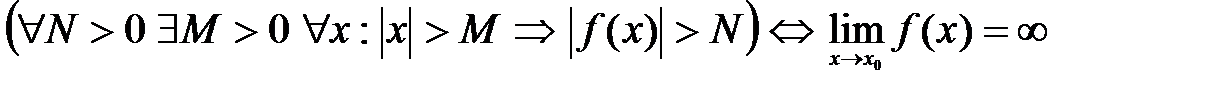 .
.
Подобным образом определяются также пределы:
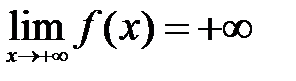 ,
, 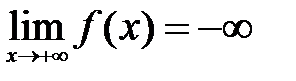 ,
, 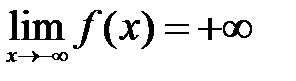 ,
, 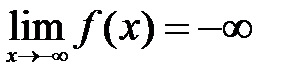 .
.
Пример 4.3. Примеры бесконечно больших функций:
а) 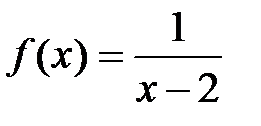 при
при 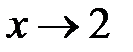 ; б)
; б) 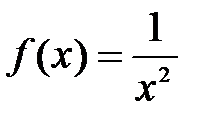 при
при 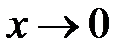 ; в)
; в) 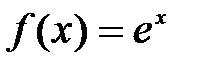 при
при 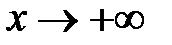 .
.
 2018-01-08
2018-01-08 530
530








